5th Class Mathematics Number System and its Operations Number System

LEADING OBJECTIVES

This lesson -will help you to:

• learn to find place value in numbers beyond 1000.
• study and learn the role of place value in addition, subtraction and multiplication algorithms.
• understand and study about informal and standard division algorithm.
• learn and study about factors and multiples.

 

Amazing Facts

• Zero was not even considered a number for the Ancient Greeks. However, they also questioned whether 1 was a number.
• The Mayans discovered/ developed zero.
• 2 and 5 are the only prime numbers that end with a 2 or a 5.
• Different names for the number 0 include zero naught, naught, nill zilch and zip.
• The name of the popular search engine ‘Google’ came from a misspelling of the word ‘googol’ which is a very large number (the number one followed by one hundred zeros to be exact)

 

QUICK CONCEPT WIEW

PLACE VALUE

B The value of the place, or position, of a digit in a number or series is called place value. Each place has a value of 10 times the place to its right.

The idea of place value is at the heart of our number system.

 

The concept of place value is as follows:

Beginning with the ones place at the right, each place value is multiplied by increasing powers of 10. For example, the value of the first place on the right is "one" the value of the place to the left of it is "ten," which is 10 times 1. The place to the left of the tens place is hundreds, which is 10 times 10, and so forth.

The place value of number goes beyond 1000 with the next place value being 10 times greater. The place values after thousand are ten thousands (10,000), hundred thousand (1,00,000), millions (10,00,000) and so on.

For easier readability, commas are used to separate each group of three digits, which is called a period. When a number is written in this form, it is said to be in "standard form" Example: four hundred sixteen thousand, seven hundred thirty-one can be written as 416,731.    

 

The role of place value in addition, subtraction and multiplication algorithms.                             

• The place value of a number starts from right to left in the following order: ones, tens, hundreds, thousands, ten thousands, hundred thousands, etc.
• Place values are extremely important when doing addition, subtraction and multiplication.
• When doing addition or subtraction, add or subtract like places, and you may need to group in addition and ungroup in subtraction to get enough to subtract from.

 

Misconcept/concept

Misconcept:  Numeral 1 is a prime number

Concept: 1 is neither prime nor composite. It does not have any factors except the number itself.

Misconcept: All prime numbers are odd numbers.

Concept: This is not true, since the number 2 has only 2 factors, 1 and 2, and is also an even number. 

 

Example: Add 65,000 and 1500         

\[\frac{\begin{align}

  & 65,000 \\

 & +1,500 \\

\end{align}}{66,500}\]

 

   Example: Subtract 7,400 from 74,000.                 

\[\frac{\begin{align}

  & 74,000 \\

 & -7,400 \\

\end{align}}{66,500}\]

Role of place value in multiplication algorithms

• The number to be multiplied is the multiplicand.
• The number we are multiplying with is the multiplier.
• Multiplication is repeated addition. Adding multiplicand by multiplier times gives the product.

Let’s us understand the concept of place value in multiplication, with the help of an example.

 

Example: Multiply the following numbers: 263 and 64

STEP 1: Multiply the multiplicand by ones digit of the multiplier.

1. Multiply the number in the ones place of the multiplicand with the number in the ones place of the multiplier.

  \[\left( 263\times 64 \right)\]

\[3\times 4=12\]

(1 tens, 2 ones).

Put the 2 in one’s column and carry over 1 to the tens column.

 

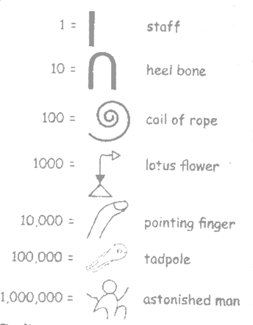
Historical preview

• The Egyptians had a base 10 system of hieroglyphs for numerals. There was no symbol for zero. They had seven separate symbols (hieroglyphs) for one unit, one ten, one hundred, one thousand, one ten thousand one hundred thousand, and one million as shown below:

 

• Indians were the first to develop a base ten system. They developed methods of expressing every possible number using a set of ten symbols very similar to the decimal system we use today with symbols close to the ones we use today. Zero was used to denote an empty space.

1	2	3	4	5	6	7	8	9
-	=		+

 

Brahmi numerals around 1^st century A.D.

2. Multiply the number in the tens place of the multiplicand with the number in the ones place of the multiplier.

 \[\left( 263\times 64 \right)\]

 \[6\times 4=24+1\]

 (carry over from step 1)

          = 25 (2 hundreds^ tens).

Put the 5 in tens column and carry over 2 to the hundreds column.

3. Multiply the number in the hundreds place of the multiplicand with the number in the ones place of the multiplier.

 \[\left( 263\times 64 \right)\]

 \[2\times 4=8+2\]

  (carry over from step 2)

 = 10 (1 thousands, 0 hundreds).

Put the 0 in hundreds column and 1 (carry over) in thousands column

 

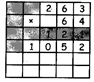
STEP 2: Multiply the multiplicand by tens digit of the multiplier

1. Multiply the number in the ones place of the multiplicand with the number in the tens place of the multiplier.

  \[\left( 263\times 64 \right)\]

  \[3\times 6=18\]

 (1 hundreds, 8 tens).

Put the 8 in tens column and carry over 1 to the hundreds column.

2. Multiply the number in the tens place of the multiplicand with the number in the tens place of the multiplier.

 \[\left( 263\times 64 \right)\]

 \[6\times 6=36+1\]

 (carry over from step 1)

= 37 (3 thousands, hundreds).

Put the 7 in hundreds column and carry over 3 to the thousands column.

3. Multiply the number in the hundreds place of the multiplicand with the number in the tens place of the multiplier.

 \[\left( 263\times 64 \right)\]

\[2\times 6=12+3\]

 (carry over from step 2)

= 15 (1 ten thousands^ thousands).

Put the 5 in thousands column and 1 (carry over) in ten thousands column.

 

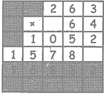
STEP 3: Add result of Multiplier 1's and Multiplier 10's results and put the result in the Product columns.

1052 + 15780 = 16832

Product of 263 and 64 is 16832

 

To study about informal and standard division algorithm

• Division is equal distribution of a given quantity.
• The number to be divided is the dividend.
• The number which divides is called divisor.
• The answer is called the quotient.
• The number left after division is called the remainder.

 

Standard Division Algorithms

Unlike addition, subtraction and multiplication, division is performed from left to right.

(Highest place value to lowest place value).

 

FACTOR AND MULTIPLES

A factor is simply a number that is multiplied to get a product. Factoring a number means taking the number apart to find its factors — it's like multiplying in reverse.

Here are lists of all the factors of 16, 20, and 45.

16 \[\to \],2,4,8,16

20 \[\to \] 1, 2,4, 5,10, 20

45 \[\to \] 1,3,5,9,15,45

Factors are either composite numbers or prime numbers.

Prime .number : A prime number has only two factors, one and itself, so it cannot be divided evenly by any other numbers. Here's a list of prime numbers up to 100.

 

Prime numbers to 100

2, 3, 5, 7,11,13,17,19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

These numbers cannot be factored any further.

Composite numbers: A composite number is any number that has more than two factors. These numbers can all be factored further. For example, 4 equals 2 times 2, 6 equal 3 times 2, 8 equals 4 times 2, and so forth.

Here's a list of composite numbers up to 20.

 

Composite numbers up to 20

1. 6, 8, 9,10,12,14,15,16,18, 20

Composite numbers can be written as a product of prime factors. This is called prime factorization. To find the prime factors of a number, you divide the number by the smallest possible prime number and work up the list of prime numbers until the result is itself a prime number.

Example: Find the prime factors of 168.

Since 168 is even, we start by dividing it by the smallest prime number, 2. 168 divided by 2 is 84. 84 divided by 2 is 42. 42 divided by 2 is 21. Since 21 is not divisible by 2, we try dividing by 3, the next biggest prime number. 21 divided by 3 equals 7, and 7 is a prime number. Therefore, 168 is now fully factored.

                                                                                            \[168\div 2=84\]

                                                                                             \[84\div 2=42\]

                                                                                             \[42\div 2=21\]

                                                                                              \[21\div 3=7\]

 Prime number prime factors =

                                                                      \[2\times 2\times 2\times 3\times 7\]

To check the answer, multiply these factors and make sure they equal 168.

Greatest Common Factor: The greatest common factor, or GCF, is the greatest factor that divides two numbers. To find the GCF of two numbers:

1. List the prime factors of each number.
2. Multiply those factors both numbers have in common. If there are no common prime factors, the GCF is 1.

Example:

Find the GCF of 18 and 24.

Prime factors of

                                                                                   \[18=2\times 3\times 3\]

Prime factors of

                                                                           \[24=2\times 2\times 2\times 3\]

There is one 2 and one 3 in common. Therefore, the 6CF =

                                                                                            \[2\times 2=6.\]

 

DIVISIBILITY RULES

The simple divisibility rules will help you to find factors of a number.

The number is divisible by:

• 2 if the last digit is 0, 2, 4, 6, or 8

     (example: 12346);

• 3 if the sum of digits in the number are divisible by 3

         (example: 1236, because

                                                                                  \[1+2+3+6=12=3\times 4\]

);

• 4 if the last 2 digits are divisible by 4 (example: 897544, because

                                                                                          \[44=4\times 11\]

• );
• 5 if the last digit is 0 or 5

         (example: 178965 or 40980);

• 6 if it is divisible by 2 and 3;
• 7 sorry, no rule (you have to divide);
• 8 if the last 3 digits are divisible by 8

          (example: 124987080, because

                                                                                         \[080=8\times 10;\]

• 9 if the sum of digits is divisible by 9

         (example: 234612, because

        

                                                                           \[2+3+4+6+1+2=18=9\times 2);\]

• 10 if the last digit is 0

         (example: 99990);

• 100 if the last 2 digits are 0

         (example: 987600);

 

MULTIPLES

• Multiple of any number is a number which can be divided exactly by that number.
• The Multiples of a number are formed by multiplying it with other numbers like l,2,3,etc.
• A number can have unlimited multiples.
• Each number is a multiple of itself.
• Every number is a multiple of 1.
• Zero is a multiple of every number.
• First multiple of every number is the number itself. So a multiple of a number cannot be less than the number.
• Multiples of any number are infinite.

How to find multiples of a given number?

Multiply the given number by 1, 2, 3, etc. The products are multiple of the given number.

Example: Multiple of 3 are 3

   \[\left( =3\times 1 \right),6\left( =3\times 2 \right),9\left( =3\times 3 \right),12\left( =3\times 4 \right),\]

etc.

 

LOWEST COMMON MULTIPLE (LCM)

• It is also called Least Common Multiple or Smallest Common Multiple.
• The smallest common multiple of two or more numbers is called the LCM (Lowest Common Multiple) or the smallest number that can be divided by the given two or more numbers.
• LCM of two integers a and b is the smallest positive integer that is a multiple of both of a and of b. Since it is a multiple, it can be divided by a and b without a remainder.

 

Some important points about multiples:

• It can be used to find the lowest common denominator when adding or subtracting fractions.
• If any of the given number is 0 (zero) then the LCM of the numbers is also 0 (zero).
• LCM (Lowest Common Multiple) is also known by least common multiple or smallest common multiple.

 

How to find LCM of the given numbers.

1. Find the prime factors of the given numbers.
2. Select all the factors which are common to at        

                  Least two numbers once.

3. Select all the factors which are not common to at least two numbers.
4. Multiply all the selected factors. The result is 

                  The LCM of the given numbers.

Example: Find LCM of 10, 15 and 18.

Prime factors of 10: 2, 5

Prime factors of 15: 3, 5

Prime factors of 18: 2, 3, 3

Factors which are common to at least two numbers: 2, 3, 5

Factors which are not common to at least two numbers: 3

LCM =

 \[2\times 3\times 5\times 3=90\]

VARIABLES: A variable is a symbol for a number we don't know yet. It is usually an alphabet.

Example: in x + 2 = 6, x is the variable.

If it is not a variable it is called a constant.