question_answer 67)

                  A cricket fielder can throw the cricket ball with a speed \[{{\upsilon }_{0}}\]. If he throws the ball while running with speed u at an angle \[\theta \] to the horizontal, find (a) the effective angle to the horizontal at which the ball is projected in air as seen by a spectator.                 (b) what will be time of flight? (c) what is the distance (horizontal range) from the point of projection at which the ball will land? (d) find  \[\theta \] at which he should throw the ball that would maximize the horizontal range as found in (iii). (e) how does \[\theta \] for maximum range change if \[u>\,{{\upsilon }_{0}},\,\,\,u<\,{{\upsilon }_{0}}?\] (f) how does  \[\theta \] in (e) compare with that for \[u=O\] (i.e., \[{{45}^{o}}\])?

Answer:

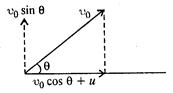
                  (a) \[\tan \,\theta =\,\frac{{{\upsilon }_{0}}\,\sin \theta }{{{\upsilon }_{0}}\,\cos \theta +\,u}\]                 or \[\theta =\,{{\tan }^{-1}}\,\left[ \frac{{{\upsilon }_{0}}\,\sin \,\theta }{{{\upsilon }_{0}}\sin \,\theta +\,u} \right]\]                 (b) Time of flight, \[T=\,\frac{2{{\upsilon }_{y}}}{g}\,\,=\,\frac{2{{\upsilon }_{0}}\,\sin \theta }{g}\]                 (c) Range,  \[R=\,({{\upsilon }_{0}}\,\cos \theta +\,u)\]  \[T=\,\frac{({{\upsilon }_{0}}\,\cos \theta \,+\,u)\,\,2{{\upsilon }_{0}}\,\sin \theta }{g}\,\]                 \[=\,\frac{2{{\upsilon }_{0}}\,\,\sin \,\theta \,({{\upsilon }_{0}}\,\cos \theta +\,u)}{g}\] (d) \[{{\left. \frac{dR}{d\theta } \right|}_{when\,R=\,{{R}_{\max }}}}=\,0\] or \[\frac{2{{\upsilon }_{0}}}{g}\,[\cos \theta \,({{\upsilon }_{0}}\,\cos \,\theta \,+\,u)\,+\,\sin \,\theta \]\[\,(-{{\upsilon }_{0}}\,\sin \theta )]\,=0\] or \[\cos \theta \,({{\upsilon }_{0}}\,\cos \theta \,+u)\,=\,{{\upsilon }_{0}}\,{{\sin }^{2}}\theta \] or \[{{\upsilon }_{0}}\,{{\cos }^{2}}\theta \,+\,u\,\,\cos \theta \,={{\upsilon }_{0}}\,{{\sin }^{2}}\,\theta \]\[=\,{{\upsilon }_{0}}\,(1-\,{{\cos }^{2}}\theta )\] \[\therefore \] \[2\,{{\upsilon }_{0}}\,{{\cos }^{2}}\theta \,+\,u\,\cos \theta \,-\,{{\upsilon }_{0}}=0\] or \[\cos \,\theta =\,\frac{-u\,\pm \,\,\sqrt{{{u}^{2}}+8\,\upsilon _{0}^{2}}}{4{{\upsilon }_{0}}}\]                          ?(i)                 \[\therefore \] \[\theta =\,{{\cos }^{-1}}\,\left[ \frac{-u\pm \,\sqrt{{{u}^{2}}+\,8\,\upsilon _{0}^{2}}}{4{{\upsilon }_{0}}} \right]\]                  ? (ii) (e) When \[u>\,{{\upsilon }_{0}},\,\,\cos \theta =\,0\] or \[\theta =\pi /2\] when \[u<\,{{\upsilon }_{0}},\,\cos \theta \,=\,\left( \frac{1}{\sqrt{2}}-\frac{u}{4{{\upsilon }_{0}}} \right)\] or \[\theta \,=\,{{\cos }^{-1}}\,\left( \frac{1}{\sqrt{2}}-\,\frac{u}{4{{\upsilon }_{0}}} \right)\]                 (f) When \[u=0,\] then \[\cos \theta =\frac{1}{\sqrt{2}}\] or \[\theta =\,{{45}^{o}}\].