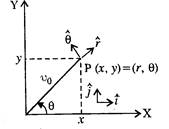
 (a) Express \[\hat{i}\,\,and\,\hat{j}\]
in terms of \[\hat{r}\,\,and\,\hat{\theta }.\]
(b) Show that both \[\hat{r}\,\,and\,\hat{\theta
}\]are unit vectors and are perpendicular to each other.
(c) Show that \[\frac{d}{dt}\,(\hat{r})\,=\,\omega
\hat{\theta }\] where
\[\omega =\,\frac{d\theta
}{dt}\] and \[\frac{d}{dt}\,\,(\hat{\theta })\,\,=-\,\omega r\]
(d) For a particle
moving along a spiral given by \[r=a\theta \hat{r},\] where \[a=1\](unit),
find dimensions of \['a'\] .
(e) Find velocity
and acceleration in polar vector representation for particle moving along
spiral described in (d) above.
(a) Express \[\hat{i}\,\,and\,\hat{j}\]
in terms of \[\hat{r}\,\,and\,\hat{\theta }.\]
(b) Show that both \[\hat{r}\,\,and\,\hat{\theta
}\]are unit vectors and are perpendicular to each other.
(c) Show that \[\frac{d}{dt}\,(\hat{r})\,=\,\omega
\hat{\theta }\] where
\[\omega =\,\frac{d\theta
}{dt}\] and \[\frac{d}{dt}\,\,(\hat{\theta })\,\,=-\,\omega r\]
(d) For a particle
moving along a spiral given by \[r=a\theta \hat{r},\] where \[a=1\](unit),
find dimensions of \['a'\] .
(e) Find velocity
and acceleration in polar vector representation for particle moving along
spiral described in (d) above.
Answer:
(a) \[\hat{r}\,\,=\,\,\cos
\,\theta \,\hat{i}\,+\,\sin \theta \hat{j}\] ?. (i)
\[\hat{\theta }\,=-\,\sin
\,\theta \hat{i}+\,\cos \,\theta \hat{j}\] ?
(ii)
Multiplying eqn.
(i) by \[\sin \theta \] and
eqn. (ii) by \[\cos \theta \] and adding, we get
\[\hat{j}\,=\,\hat{r}\,\sin
\,\,\theta +\,\hat{\theta }\,\,\cos \,\theta \] ... (iii)
Put this value in
eqn. (i), we get
\[\hat{i}=\hat{r}\,\cos
\theta -\,\hat{\theta }\,\sin \,\theta \] ... (iv)
(b) \[|\hat{r}|\,\,=\hat{r}.\,\hat{r}\,=1\]
and \[|\hat{\theta
}|\,=\,\hat{\theta }.\,\hat{\theta }\,\,=1\]
Since magnitude of
both \[\hat{r}\] and
\[\hat{\theta }\] in
unity (1), so they are unit vectors, \[\hat{r}\] and \[\hat{\theta }\] will be
perpendicular to each other if \[\hat{r}\,.\,\hat{\theta }\,=0\]
Now \[\hat{r}.\,\hat{\theta
}\]
\[=\,(\cos \,\theta
\hat{i}+\,\sin \,\theta \hat{j})\,.\,(-\,\sin \,\theta \hat{i}\,+\,\cos \theta
\hat{j})\]
\[=-\,\sin \,\theta
\,\,\cos \,\,\theta +\,\sin \theta \,\cos \theta =0\]
\[(\because
\,\,\,\hat{i}\,.\,\hat{i}\,=\,\hat{j}\,.\,\hat{j}\,=1\,\,\text{and}\,\,i\,.\,\hat{j}\,=\,j.\,\hat{i}\,=0)\]
Therefore, \[\hat{r}\]
and \[\hat{\theta
}\] are
perpendicular to each other.
(c) \[\frac{d}{dt}\,(\hat{r})\,\,=\,\frac{d}{dt}\,(\cos
\,\theta \,\hat{i}\,+\,\sin \,\theta \,\hat{j})\]
\[=(-\sin \theta
)\,\frac{d\theta }{dt}\,\hat{i}\,+\,(\cos \theta )\,\frac{d\theta
}{dt}\,\hat{j}\]
\[=\,\frac{d\theta
}{dt}\,[-\sin \theta \,\hat{i}\,+\,\cos \,\theta \,\hat{j}]\]
Since \[\frac{d\theta
}{dt}\,\,=\,\omega \] and
\[-\,\sin \,\theta \hat{i}\,+\,\cos \theta \hat{j}\,=\hat{\theta }\]
\[\therefore
\]\[\frac{d}{dt}\,\,(\hat{r})=\,\omega \hat{\theta }\]
\[\frac{d}{dt}\,(\hat{\theta
})=\,\frac{d}{dt}\,(-\,\sin \,\theta \hat{i}\,+\,\cos \theta \hat{j})\]
\[=-\frac{d\theta
}{dt}\,\,\cos \,\theta \,\hat{i}\,-\,\frac{d\theta }{dt}\,\sin \,\theta
\,\,\hat{j}\]
\[=-\,\frac{d\theta
}{dt}\,(\cos \theta \,\hat{i}\,+\,\sin \,\theta \hat{j})\]
\[=-\omega \,\hat{r}\] [using eqn. (i)]
(e) \[\vec{r}\,=a\,\,\theta
\,\,\,\hat{r}\,=\,\theta \,\,\,\hat{r}\] \[(\because
\,\,a=1)\]
\[\therefore \] \[\vec{\upsilon
}\,=\,\frac{d\,\,\vec{r}}{dt}=\,\theta
\,\frac{d\hat{r}}{dt}+\,\hat{r}\,\frac{d\theta }{dt}\] ... (i)
Since \[\frac{d\hat{r}}{dt}=\omega
\,\hat{\theta }\] and
\[\frac{d\theta }{dt}=\,\omega \]
\[\therefore \] \[\vec{\upsilon
}=\,\omega \,\theta \,\hat{\theta }\,+\,\omega \,\hat{r}=\,\omega
\,(\hat{r}\,+\,\theta \,\,\hat{\theta })\]
Acceleration, \[\vec{a}\,\,=\,\frac{d\vec{\upsilon
}}{dt}=\frac{d}{dt}\,(\omega \,\hat{r}+\,\omega \theta \,\,\hat{\theta })\]
\[=\,\hat{r}\,\frac{d\omega
}{dt}+\omega \,\frac{d\hat{r}}{dt}+\,\omega \,\frac{d\theta }{dt}\,\hat{\theta
}\] \[+\,\frac{d\omega }{dt}\,\theta \,\hat{\theta }+\,\omega \theta
\,\frac{d\hat{\theta }}{dt}\]
Since \[\frac{d\theta
}{dt}=\omega ,\,\,\frac{d\hat{r}}{dt}=\omega \,\hat{\theta }\] and \[\frac{d\hat{\theta
}}{dt}\,=\,-\omega \,\hat{r}\]
\[\therefore
\]\[\,\vec{a}=\,\hat{r}\,\frac{d\omega }{dt}+\,{{\omega }^{2}}\hat{\theta
}+\,{{\omega }^{2}}\,\hat{\theta }+\,\frac{d\theta }{dt}\,\theta \,\hat{\theta
}\,-\,{{\omega }^{2}}\,\theta \,\hat{r}\]
\[=\,\hat{r}\,\,\left(
\frac{d\omega }{dt}-\,{{\omega }^{2}}\theta \right)\,+\,\hat{\theta }\,\left(
\theta \,\frac{d\omega }{dt}+\,2{{\omega }^{2}} \right)\]
Now \[=\,\hat{r}\,\,\left(
\frac{d\omega }{dt}-\,{{\omega }^{2}}\theta \right)\,+\,\hat{\theta }\,\left(
\theta \,\frac{d\omega }{dt}+\,2{{\omega }^{2}} \right)\]
\[\therefore
\]\[\vec{a}=\,\hat{r}\left( \frac{{{d}^{2}}\theta }{d{{t}^{2}}}-{{\omega
}^{2}}\theta \right)\,\,+\hat{\theta }\,\left( \theta \frac{{{d}^{2}}\theta
}{d{{t}^{2}}}+2{{\omega }^{2}} \right)\]
You need to login to perform this action.
You will be redirected in
3 sec
