10th Class Mathematics Quadratic Equations Quadratic Equation

 QUADRATIC EQUATION

FUNDAMENTALS

• Quadratic equation: An equation of the form \[a{{x}^{2}}+bx+c=0\] where a, b, and c \[\in \] R and \[a\ne 0\]is called a quadratic equation.

Note: (i) An equation of degree 2 is called a quadratic equation.

   (ii) The quadratic equation is of the form\[a{{x}^{2}}+bx+c=0\].

• Solution or roots of a quadratic equation: If p(x) = 0 is a quadratic equation, then the zeros of the polynomial p(x) are called the solutions or roots of the quadratic equation P(x) = 0.

Note: (i) Since the degree of a quadratic equation is 2, if has 2 roots or solutions.

   (ii) \[x=a\]is the root of \[p\left( x \right)=0,\]if \[p\left( a \right)=0.\]

   (iii) Finding the roots of a quadratic equation is called solving the quadratic equation.

• Methods of solving a quadratic equation: There are different methods of solving a quadratic equation.

(a) Factorization method by:

(i) Splitting the middle term                      (ii) Completing the square

            (b) Using formula for roots \[(\alpha ,\beta )=\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}\]

1. (i) Splitting the middle term: Consider the quadratic equation \[a{{x}^{2}}+bx+c=0\].

Step 1: Find the product of the coefficient of \[{{x}^{2}}\] and the constant term i.e., ac.

Step 2: (a) If ac is positive, then choose two factors of ac, whose sum is equal to b (the coefficient of the middle term).

(b) If ac is negative, then choose two factors of ac, whose difference is equal to b (the coefficient of the middle term).

Step 3: Express the middle terms as the sum (or difference) of the two factors obtained in step 2. [Now the quadratic equation has 4 terms]

Step 4: Express the given quadratic equation as a product of two binomials, and solve them. The two values obtained in step 2 are the roots of the given quadratic equation.

Elementary question - 1: Solve \[{{x}^{2}}+7x+12=0\]

Answer; ac = 1.12 = 12: Factors are 1, 2, 3, 4, 6, 12

The combination which gives middle term b =7 is 3 + 4 = 7

\[\therefore \] Written as \[{{x}^{2}}+3x+4x+12=0\]

or \[x\left( x+3 \right)+4\left( x+3 \right)=0\text{ }or\text{ }\left( x+4 \right)\left( x+3 \right)=0\]

(ii)         Completing the square: In some cases, where the given quadratic equation can be solved by factorization, a suitable term is added and subtracted. Then terms are regrouped in such a manner that a square is completed by three of the terms. The equation is then solved using factorization method.

Usually, the term added and subtracted is the square of half the coefficient of x.

1. Formula method: The roots of a quadratic equation \[a{{x}^{2}}+bx+c=0\] are given by\[\frac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a},\]provided \[{{b}^{2}}-4ac\ge 0\]. This formula for finding the roots of a quadratic equation is called the quadratic formula.

Note:    The roots of the quadratic equation using the quadratic formula are \[x=\frac{-b+\sqrt{{{b}^{2}}-4ac}}{2a}\] and \[x=\frac{-b-\sqrt{{{b}^{2}}-4ac}}{2a}\]

Roots of Biquadratic Equation

Any biquadratic equation, \[a{{x}^{4}}+b{{x}^{3}}+c{{x}^{2}}+dx+e=0,\] will have four roots. If a, p, y and 5 are its roots, the relation between the roots is given by

Sum of the roots \[=\alpha +\beta +\gamma +\delta =-\frac{b}{a}\]

Sum of product of two roots at a time \[=\alpha \beta +\beta \gamma +\gamma \delta +\delta \alpha =\frac{c}{a}\]

Sum of product of three roots at a time \[=\alpha \beta \gamma +\beta \gamma \delta +\gamma \delta \alpha +\delta \alpha \beta =-\frac{d}{a}\]

Product of the roots \[=\alpha \beta \gamma \delta =\frac{e}{a}\]

Constructing a New Quadratic Equation by Changing the Roots of a Given Quadratic Equation

If we are given a quadratic equation, we can build a new quadratic equation by changing the roots of this equation in the manner specified to us.

For example, consider the quadratic equation \[a{{x}^{2}}+bx+c=0\] and let its roots be \[\alpha \] and \[\beta \] respectively. Then, we can build new quadratic equations as per the following points.

1. A quadratic equation whose roots are \[\frac{1}{\alpha }\] and \[\frac{1}{\beta }\], i.e., the roots are reciprocal to the roots of the given quadratic equation can be obtained by substituting \[\left( \frac{1}{x} \right)\] for x in the given equation, which gives us \[c{{x}^{2}}+bx+a=0,\] i.e., we get the equation required by interchanging the coefficient of \[{{x}^{2}}\] and the constant term.
2. A quadratic equation whose roots are \[\left( \alpha +k \right)\] and \[\left( \beta +k \right)\] can be obtained by substituting \[\left( x-k \right)\] for x in the given equation.
3. A quadratic equation whose roots are \[\left( \alpha -k \right)\] and \[\left( \beta -k \right)\] can be obtained by substituting \[\left( x+k \right)\] for x in the given equation.
4. A quadratic equation whose roots are \[\left( k\alpha \right)\] and \[\left( k\beta  \right)\] can be obtained by substituting \[\left( \frac{x}{k} \right)\] for x in the given equation.
5. A quadratic equation whose roots are \[\left( \frac{\alpha }{k} \right)\] and \[\left( \frac{\beta }{k} \right)\] can be obtained by substituting (kx) for x in the given equation.
6. A quadratic equation whose root are \[\left( -\alpha \right)\] and \[\left( -\beta  \right)\] can be obtained by replacing x by \[\left( -x \right)\] in the given equation.

Finding the roots of a quadratic equation by Graphical Method

Method

We can also solve the quadratic equation \[p{{x}^{2}}+qx+r=0\]by considering the following equation: Clearly, \[y=p{{x}^{2}}\]is a parabola and \[y=-qx-r\]is a straight line

Step 1: Draw the graph of \[y=p{{x}^{2}}\]and \[y=-qx-r\]on the same graph paper.

Step 2: Draw perpendiculars from the points of intersection of parabola and the straight line onto the X-axis. Let the points of intersection on the X-axis be \[\left( {{x}_{1}},0 \right)\] and\[\left( {{x}_{2}},0 \right)\].

Step 3: The x-coordinates of the points in Step (2), i.e., \[{{x}_{1}}\] and \[{{x}_{2}}\] are the two distinct roots of \[p{{x}^{2}}+px+r=0\]

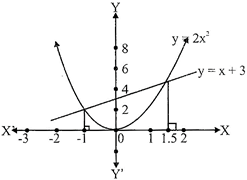
Example:

Solve \[2{{x}^{2}}-x-3=0\]

We know that the roots of \[2{{x}^{2}}-x-3=0\] are the x-coordinates of the points of intersection of the parabola, \[y=2{{x}^{2}}\]and the straight line, \[y=x+3\]

Draw the graph of \[y=2{{x}^{2}}\] and \[y=x+3\](see Fig.)

Clearly, the perpendiculars drawn from the points of intersection of parabola and the line meet the X-axis at\[\left( \frac{3}{2},0 \right)\] and \[(-1,0)\].

\[\therefore \] The roots of the given quadratic equation \[2{{x}^{2}}-x-3=0\] are \[\frac{3}{2}\] and – 1.

Note:

1. If the line meets the parabola at two points, then the roots of the quadratic equation are real and distinct.

2. If the line touches the parabola at only one point, then the quadratic equation has real and equal roots (see figure).

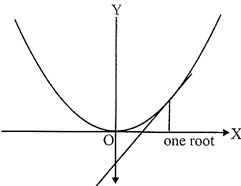
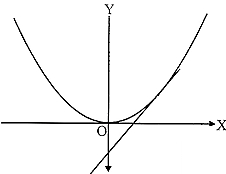
3. If the line does not meet the parabola, i.e., when the line and the parabola have no points in common, then the quadratic equation has no real roots. In this case, the roots of the quadratic equation are imaginary (see Figure)