Surface Area and Volume (Mensuration)
Category : 10th Class
Surface Area and Volume (Mensuration)
FUNDAMENTAL
Volume of a Solid
The amount of space enclosed by the bounding surface or surfaces of a solid is called the volume of the solid and is measured in cubic units. For e.g., the amount of water in litres (which is measured in cu.dm.) in a fully filled glass of water, represents volume of glass.
Note: To keep you familiar with NCERT (which is the base book for CBSE), we have included portions of NCERT, at a few places, with some modifications.
We will basically be studying THREE categories of solids - PRISMS, PYRAMIDS and SPHERES. Lastly, we will touch little on POLYHEDRONS without going into much details.
What is a prism?
A prism is a solid in which two congruent and parallel polygons form the top and the bottom faces and its lateral faces are parallelograms.
Examples are:
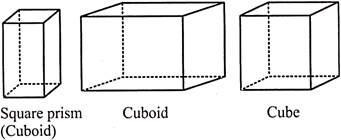
(i) Cube in which congruent faces are squares and lateral faces are squares.
(ii) Cuboid: Congruent faces = Rectangles; Lateral faces = Rectangles.
(iii) Square prism: Congruent faces = Squares (a type of cuboid): Lateral faces = Rectangles.
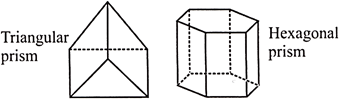
(iv) Alar prism: Congruent faces = Triangles; Lateral faces = || gms
If two parallel and congruent polygons are regular and if the axis is perpendicular to the base, then the prism is called a right prism. The lateral surfaces of a right prism are rectangles.
Note: The following points hold good for all prisms.
LSA = Lateral Surface Area = Perimeter of base x height; TSA = Total Surface Area
CUBES AND CUBOIDS
Cuboid
V = 1 b h; where 1 = length; b = breadth & h = height
LSA of cuboid \[=2(l+b)h\]
TSA of cuboid \[=2(l+b)h+2lb=2lb+2bh+2lh\]
Diagonal of a cuboid \[=\sqrt{{{1}^{2}}+{{b}^{2}}+{{h}^{2}}}\] units.
Note: If a closed box made of wood of thickness t has inner dimensions of I, b and h, then the outer length = l + 2t, then outer breadth = b + 2t and the outer height = h + 2t.
Cube: It is a special case of a cuboid
In a cuboid, if all the dimensions, i.e., its length, breadth and height are equal, then it is called a cube.
Here, l = b = h = ‘a’
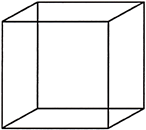
\[\therefore \] If the edge of a cube is a units, then, Volume \[={{a}^{3}}\]and, LSA \[=4{{a}^{2}}\].
TSA = LSA + 2 (Area of base) \[=4{{a}^{2}}+2{{a}^{2}}=6{{a}^{2}}\].
Diagonal of the cube \[=\sqrt{{{a}^{2}}+{{a}^{2}}+{{a}^{2}}}=\sqrt{3}a\].
Note: If the inner edge of a cubical box made of wood of thickness ‘t’ is 'a' units, then the outer edge of the cube is given by a + 2t units.
RIGHT CIRCULAR CYLINDER
A cylinder comprises two congruent and parallel circular regions which are connected by a curved surface. It is a special kind of right prism in which congruent faces are circles. Each of the circular regions is called the base of the cylinder. A road roller, water pipe, power cable, round pillar are examples of cylindrical objects.
The radius ‘r’ of the base of the cylinder and its height ‘h’, completely describe the cylinder.
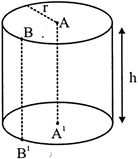
V = Area of base \[\times \] height \[=\pi {{r}^{2}}h\]
LSA of cylinder \[=2\pi r.h\]
TSA of cylinder = LSA + 2(Base area) \[=2\pi rh+2(\pi {{r}^{2}})=2\pi r(r+h)\]
Note: If a plastic pipe of length I is such that its outer radius is R and the inner radius is r, then the volume of the plastic content of the pipe is \[\pi \left( {{R}^{2}}-{{r}^{2}} \right)\]. L
Example:
A closed cylindrical pot (r = 14 cm, h = 30 cm) is to be made out of copper sheet Find
(a) The volume of the cylinder made; (b) The area of copper sheet required.
Solution
(a) Volume \[=\pi {{r}^{2}}h\]
\[=\frac{22}{7}\times {{14}^{2}}\times 30=18480\,c.c\]
(b) Area of the Copper sheet required = T.S.A. of Cylinder
\[=2\pi r(r+h)\]
\[=2\times \frac{22}{7}\times 14(14+30)=88\times 44\,c{{m}^{2}}=3872\,sq.cm.\]
RIGHT CIRCULAR CONE
In a circular cone, if the line joining the vertex and the centre of the base of the cone is perpendicular to the base, then it is called a right circular cone. In other words, if the axis of the cone is perpendicular to the base of the cone, then it is a right circular cone. The length of the line segment AO is called the height of the cone. In this chapter we deal with problems on right circular cones.
\[\therefore \] Respective formula of right pyramid becomes,
\[V=A\times h=\frac{1}{3}\pi {{r}^{2}}h\]
\[LSA=\frac{1}{2}p.l=\left( \frac{1}{2}.2\pi r \right).l=\pi rl\]
\[TSA=LSA+{{A}_{base}}=\pi rl+\pi {{r}^{2}}=\pi r(r+l)\]
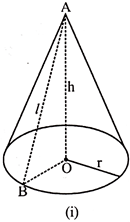
We can also defined a right circular cone as a solid obtained by the revolution of a right angled triangle about one of its two perpendicular sides.
If we consider any point B on the periphery of the base of the cone, then the line joining B and the vertex A is called the slant height of the cone and is denoted by l. Since AO is perpendicular to OB, \[\Delta \,AOB\]is right angled (Figure (ii).
As, we can see from figure, \[l=\sqrt{{{r}^{2}}+{{h}^{2}}}\]
Frustum of a Cone:
If a right circular cone is cut by a plane parallel to the base, then the solid portion containing the base of the cone is called the frustum of the cone.
We observe that a frustum is in the shape of a conical bucket.
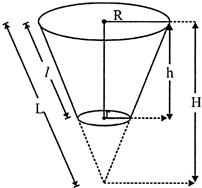
Let radius of the upper base be ‘R’, radius of the lower base be ‘r’, height of the frustum be ‘h’ and slant height of the frustum be ‘l’. If a cone is formed by extending the slant sides, then let total height be ‘H’ and total slant height be ‘L’.
SPHERE
Sphere is a locus of points in the space which are equidistant from a fixed point. The fixed point is called the centre of the sphere, and the fixed distance is called the radius of the sphere. In day-to-day life, we find spherical objects in a cricket ball, football, globe, basketball, playing marble balls, lemon, orange, moon, sun etc.
A line segment joining any two points on the surface of sphere and passing through the centre of the sphere is called the diameter of the sphere, hi the above example, marble balls, moon, sun etc. are examples of solids spheres, whereas football, basketball, globe etc. are hollow spheres.
Solid and Hollow spheres:
The centre of sphere is a part of solid sphere whereas the centre is not a part of hollow sphere.
Hemisphere
Any plane passing through the centre of sphere, will cut it into two equal parts - each part is called a hemisphere.

Formulas to Memorize
Sphere
\[V=\frac{4}{3}\pi {{r}^{3}}\];
Curved surface Area (CSA) of sphere \[=4\pi {{r}^{2}}\]
Hemisphere
\[V=\frac{2}{3}\pi {{r}^{3}};CSA=2\pi {{r}^{2}};TSA=3\pi {{r}^{2}}\]
Spherical and Hemispherical Shells
The space between two concentric solid spheres is known as spherical shell.
Volume of a Combination of Solids
In the previous section, we have discussed how to find the surface area of solids made up of a combination of two basic solids. Here, we shall see how to calculate their volumes. It may be noted that in calculating the surface areas, we have not added the surface areas of the two constituents, because some part of the surface areas disappeared in the process of joining them. However, this will not be the case when we calculate the volume. The volume of the solid formed by joining two basic solids will actually be the sum of the volumes of the constituents, as we see in the example below.
Example: A juice seller was serving his customers using glasses as shown in figure. The inner diameter of the cylindrical glass was 5 cm, but the bottom of the glass had a hemispherical raised portion which reduced the capacity of the glass. If the height of a glass was 10 cm, find the apparent capacity of the glass and its actual capacity. (Use \[\pi =3.14\].)
Solution: Since the inner diameter of the glass = 5 cm and height = 10 cm, the apparent capacity of the glass \[=\pi {{r}^{2}}h=3.14\times 2.5\times 2.5\times 10=196.40\,\,c{{m}^{2}}\]
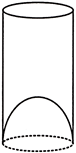
i.e., It is less by \[\frac{2}{3}\pi {{r}^{3}}=\frac{2}{3}\times 3.14\times 2.5\times 2.5\times 2.5\,\,c{{m}^{2}}=32.71\,\,c{{m}^{3}}\]
So, the actual capacity of the glass = apparent capacity of glass – volume of the hemisphere
\[=(196.25-32.71)\text{ }c{{m}^{3}}=163.54\text{ }c{{m}^{3}}\]
About Polyhedrons
Solids bounded by polygons are known as polyhedrons. The bounding polygons are known as the faces and the intersection of the faces are edges. Intersection of three or more edges is known as a vertice.
Types of Polyhedrons:
|
Polyhedron with 4 faces |
= |
Tetrahedron |
|
Polyhedron with 6 faces |
= |
Hexahedron |
|
Polyhedron with 8 faces |
= |
Octahedron |
|
Polyhedron with 10 faces |
= |
Decahedron |
|
Polyhedron with 12 faces |
= |
Dodecahedron |
If all the faces of a polyhedron are congruent regular polygons, then it is a regular polyhedron.
(Utility: These 3D figures find practical utility in your chemistry of higher classes).
Regular Tetrahedron
The lateral surface area of a regular tetrahedron \[=\frac{1}{2}\times \] Perimeter of base \[\times \] Slant height
\[\text{=}\frac{\text{1}}{\text{2}}\text{ }\!\!\times\!\!\text{ 3a }\!\!\times\!\!\text{ }\frac{\sqrt{\text{3}}}{\text{2}}\text{a=}\frac{\text{3}\sqrt{\text{3}}}{\text{4}}{{\text{a}}^{\text{2}}}\] (where ‘a’ is the edge).
The total surface area of a regular tetrahedron = LSA + Area of base.
\[\text{=}\frac{\text{3}\sqrt{\text{3}}}{\text{4}}{{\text{a}}^{\text{2}}}\text{+}\frac{\sqrt{\text{3}}}{\text{4}}{{\text{a}}^{\text{2}}}\text{=}\sqrt{\text{3}}{{\text{a}}^{\text{2}}}\]
Volume of a regular tetrahedron \[\text{=}\frac{1}{3}\times \] Area of base \[\times \] Vertical height
\[\text{=}\frac{\text{1}}{\text{3}}\text{ }\!\!\times\!\!\text{ }\frac{\sqrt{\text{3}}}{\text{a}}{{\text{a}}^{\text{2}}}\text{ }\!\!\times\!\!\text{ }\frac{\sqrt{\text{2}}}{\sqrt{\text{3}}}\text{a=}\frac{{{\text{a}}^{\text{3}}}}{\text{6}\sqrt{\text{2}}}\]
Conversion of Solid from One Shape to Another
Consider the following example.
Example: A cone of height 24 cm and radius of base 6 cm is made up of modeling clay. A child reshapes it in the form of a sphere. Find the radius of the sphere.
Solution: Volume of cone \[\text{=}\frac{1}{3}\times \pi \times 6\times 6\times 24\,\,c{{m}^{2}}\]
If r is the radius of the sphere, then its volume is \[\frac{4}{3}\pi {{r}^{3}}\].
Since, the volume of clay in the form of the cone and the sphere remains the same, we have
\[\frac{4}{3}\times \pi \times {{r}^{3}}=\frac{1}{3}\times \pi \times 6\times 6\times 24\]
i.e., \[{{r}^{3}}=216\]
So, \[r=6\]
Therefore, the radius of the sphere is 6 cm.
You need to login to perform this action.
You will be redirected in
3 sec
