11th Class Mathematics Sequence & Series Notes - Mathematics Olympiads - Three Dimensional Plane

 

                                                                           Three Dimensional Plane

 

In three dimensional Geometry, it is not a new geometry though it is the refined or extension form of the two dimension geometry. In 3-dimensional geometry. Three axes i.e. x-axis, y-axis and z-axis are perpendicular to each other is considered.

Let \[X'OX',Y'OY\] & \[Z'OZ\] be three mutually perpendicular lines which be intersect at 0. It is called origin.
   

                            

 

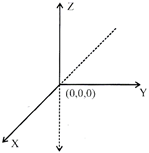
\[X'OX\xrightarrow{{}}x-axis\]

 

\[Y'OY\xrightarrow{{}}y-axis\]

 

\[Z'OZ\xrightarrow{{}}z-axis\]

 

Plane XOY is called xy plane

YOZ is called yz plane

and ZOX is called zx plane

In 3-D, there are 8 quadrents

Equation of x-axis be y= 0 & z =0

Equation of y-axis be x = 0 & z = 0

and equation of z-axis be x=0 & y=0

 

Note: In 3-D, a straight line is represented by two equations where as a plane is represented by single equation in at most three variables.

 

• Some basic formula which are used in 3-dimension. The distance between points \[A({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}})\] and \[B({{x}_{1}},\,{{y}_{2}},\,{{z}_{3}})\]be

 

\[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}\]

 

e.g. Let two points are A (2, 3, 1) & B = (- 5, 2-1)

 

            \[\therefore \,\,\,\,AB=\sqrt{{{(-5-2)}^{2}}+{{(2-3)}^{2}}+{{(-1-1)}^{2}}}\]

 

            \[=\sqrt{49+5}=\sqrt{54}\]

 

• Section Formula: The coordinate of the point P dividing the line joining \[A({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}})\] & \[({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}})\] in the ratio m:n internally are

 

\[P=\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\frac{m{{z}_{2}}+n{{z}_{1}}}{m+n} \right)\]

 

The co-ordinate of the point P dividing the line joining \[A({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}})\] and \[({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}})\] in the ratio m:n externally are

                       

\[P=\left( \frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\frac{m{{z}_{2}}-n{{z}_{1}}}{m-n} \right)\]

 

Midpoint of AB be

 

            \[P=\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2},\frac{{{z}_{1}}+{{z}_{2}}}{2} \right).\]

 

e.g.       Find the co-ordinate of the point which divides the line segment joining the point (-2, 3, 5) & (1, - 4, 6) in the ratio (i) 2: 3 internally (ii) 2:3 externally.

 

Sol.      Here, Let A= (-2, 3, 5) & B= (1, -4, 6)

and m:n =2:3 internally

Let P divides AB in the ratio m: n internally

                       

            \[\therefore \,\,\,P=\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\frac{m{{z}_{2}}+m{{z}_{1}}}{m+n} \right)\]

 

            \[=\left( \frac{2.1+3(-2)}{2+3},\frac{2(-4)+3.3}{2+3},\frac{2\times 6-3\times 5}{2+3} \right)\]

 

            \[=\left( \frac{-4}{5},\frac{1}{5},\frac{27}{5} \right)\]

 

When P divides AB in the ratio m : n externally

                       

            \[\therefore \,\,\,P=\left( \frac{2.1-3(-2)}{2-3},\frac{2(-4)-3.3}{2-3},\frac{2\times 6-3\times 5}{2-3} \right)\]

 

            \[P=(-8,+17,3).\]

 

• Controid of triangle: The co-ordinate of the centroid of the triangle ABC, whose vertices are

 

\[A({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}}),\] \[B({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}}),\] & \[C({{x}_{2}},\,{{y}_{2}},\,{{z}_{3}}),\] are

 

\[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3},\frac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3} \right)\]

 

• Centroid of the tetrahedran: If \[({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}}),\] \[({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}}),\] \[({{x}_{3}},\,{{y}_{3}},\,{{z}_{3}})\,a({{x}_{4}},\,{{y}_{4}},\,{{z}_{4}})\] be the vertices of the tetrahedran, then its centroid G is given by

 

\[\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}+{{x}_{4}}}{4},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}+{{y}_{4}}}{4},\frac{z1+z2+z3+z4}{4} \right)\]

 

1. A point R with x-coordinate 4 lies on the segment joining the points \[\mathbf{P(2,-3,4)}\] & \[\mathbf{Q(8,0,1,0)}\mathbf{.}\]

Find the co-ordinate of the point R.

 

Sol:      Let \[P(2,-3,4)\] and \[Q(8,0,1,0).\]

Let R divides PQ in the ratio l: 1 internally

 

\[\therefore \,\,\,\,R=\left( \frac{8\lambda +2}{\lambda +1},\frac{0.\lambda +(-3)}{\lambda +1},\frac{10\lambda +1\times 4}{\lambda +1} \right)\]…………  (1)

Here x co-ordinate =4

 

\[\therefore \,\,\,\,\frac{8\lambda +2}{\lambda +1}=\frac{4}{1}\]

 

\[\Rightarrow \,\,8\lambda +2=4\lambda +4\]

\[\Rightarrow \,\,8\lambda -4\lambda =4-2=2\]

\[\Rightarrow \,\,4\lambda =2\]

\[\lambda =\frac{2}{4}=\frac{1}{2}\]

 

Putting the value of \[\lambda \] in (1), we have

                       

\[R=\left( \frac{4+2}{\frac{1}{2}+1},\frac{-3}{\frac{1}{2}+1},\frac{5+4}{\frac{1}{2}+1}, \right)\]

 

\[=\left( 6\times \frac{2}{3},-3\times \frac{2}{3},9\times \frac{2}{3} \right)=(4,-2,6)\]

 

1. Find the co-ordinate of the point R on -y axis which are at distance of \[\mathbf{5}\sqrt{\mathbf{2}}\] from the point \[\mathbf{P(3,-2,5)}\]

 

Sol:      Let \[R=(0,\,b,\,0)\] on y-axis.

Given \[P(3,-2,5)\] & \[PR=5\sqrt{2}\]

By distance formula,

 

\[PR=\sqrt{{{(3-0)}^{2}}+{{(-2-b)}^{2}}+{{(5-0)}^{2}}}=5\sqrt{2}\]

 

squaring both side, we have

 

            \[9+{{(2+b)}^{2}}+25=25\times 2\]

\[9+4+{{b}^{2}}+4b+25=50\]

\[\Rightarrow {{b}^{2}}+4b+38-50=0\]

\[(b+6)(b-2)=0\]

\[\Rightarrow b=2,-6\]

Hence b =2 (b=-6 is not possible)

            \[\therefore \,\,\,R=(0,2,0)\]

 

• Direction cosines: Let P (a, b, c) be any point. We join P to origin O. Let the line OP makes an angle \[\alpha \,,\beta ,\,\gamma \] with positive direction of x-axis, y-axis and z-axis respectively. Then \[\cos \,\,\alpha \,,\] \[\cos \,\,\beta ,\]and \[\cos \,\,\gamma \]and cosy are called the direction cosine of the directed line OP. If the angle is measured in clockwise direction then the direction angles are replaced by their supplements i.e. \[\pi -\alpha ,\] \[\pi -\beta ,\] and \[\pi -\gamma \] respectively. It is generally denoted by t, m and n respectively i.e. \[\ell =\cos \alpha ,\,\,\,\,m\]

\[=\cos \beta \] and \[n=\cos \,\,\gamma \]

\[\Rightarrow \,\,\,{{\ell }^{2}}+{{m}^{2}}+{{n}^{2}}=1\]

 

Direction Ratio: The three number a, b, c proportional to the direction cosines \[\ell \], m, n of a vector are known as the direction ratio of the OP vector,

 

 

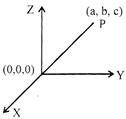
We consider P (a, b, c) be any point in the space length f from the origin to the axis is said to be direction ratio.

 

\[\therefore \,\,\,\,OP=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\] (By distance formulae)

           

\[\left| \,r\, \right|=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\]

 

Note: Direction cosine is proportional to the direction ratio. Let a, b, c be d.r. of the line OP and its d.c. be \[\ell \], m and n respectively.

 

Then \[\frac{\ell }{a}=\frac{m}{b}=\frac{n}{c}=K\] (say)

 

Convection from d.r. to D.C.

                       

\[\ell =\pm \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

 

            \[m=\pm \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

 

            and \[n=\pm \frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

 

• Some silent features about D.R. and D.C.

 

If \[\overline{r}=a\overline{i}+b\overline{j}+c\overline{z}\]

Then a, b and c be the d.r. of r and d.c. of r be

                       

            \[\ell =\frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},m=\frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\] and \[n=\frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

 

• The D.R. of the line joining two point \[P({{x}_{1}},{{y}_{1}},{{z}_{1}})\] and \[Q({{x}_{2}},{{y}_{2}},{{z}_{2}})\] are \[{{x}_{2}}-{{x}_{1}},\,\]\[{{y}_{2}}-{{y}_{1}}\] and \[{{z}_{2}}-{{z}_{1}}\] and its direction cosine (d.c.) be

 

\[\frac{{{x}_{2}}-{{x}_{1}}}{\left| PQ \right|},\frac{{{y}_{2}}-{{y}_{1}}}{\left| PQ \right|},\frac{{{z}_{2}}-{{z}_{1}}}{\left| PQ \right|}\] respectively

 

• Direction cosine of x-axis, y-axis and z-axis be written as (1, 0, 0) (0, 1, 0) and (0, 0, 1) respectively

 

• Angle between Two Vectors

 

If \[\theta \] be the angle between two vectors whose direction cosines are \[{{\ell }_{1}},\,{{m}_{1}},\,{{n}_{1}}\]and \[{{\ell }_{2}},\,{{m}_{2}},\,{{n}_{2}}\] then

\[\cos \theta ={{\ell }_{1}}{{\ell }_{2}}+{{m}_{1}}{{m}_{2}}+{{n}_{1}}{{n}_{2}}\]and

           

            \[\sin \theta =\sqrt{{{({{m}_{1}}{{n}_{2}}-{{m}_{2}}{{n}_{1}})}^{2}}+{{({{m}_{1}}{{\ell }_{2}}-{{m}_{2}}{{\ell }_{1}})}^{2}}+{{({{\ell }_{1}}{{n}_{2}}-{{\ell }_{2}}{{n}_{1}})}^{2}}}\]

 

• If \[{{\ell }_{1}}{{\ell }_{2}}+{{m}_{1}}{{m}_{2}}+{{n}_{1}}{{n}_{2}}=0\]

Then both vection be orthogonal.

 

• If \[\frac{{{\ell }_{1}}}{{{\ell }_{2}}}=\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{n}_{1}}}{{{n}_{2}}}\]

Then both vectors are parallel.

 

• Angle in the terms of direction ratio (D.R).

If \[\overline{a}={{a}_{1}}\overline{i}+{{b}_{1}}\overline{j}+{{c}_{1}}\overline{k}\]

and \[\overline{b}={{a}_{2}}\overline{i}+{{b}_{2}}\overline{j}+{{c}_{2}}\overline{k}\] be two vectors

 

\[\therefore \]      Its direction ratios be \[{{a}_{1}},\,{{b}_{1}},\,{{c}_{1}}\] and \[{{a}_{2}},\,{{b}_{2}},\,{{c}_{2}}\] respectively, q is the angle between these two vectors. Then

                       

            \[\therefore \,\,\,\,\,\,\cos \theta =\frac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}}{\sqrt{{{a}^{2}}_{1}+{{b}^{2}}_{1}+{{c}^{2}}_{1}}.\sqrt{{{a}^{2}}_{2}+{{b}^{2}}_{2}+{{c}^{2}}_{2}}}.\]

 

If two vectors are orthogonal then

 

            \[{{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}}+{{c}_{1}}.{{c}_{2}}=0\]

 

If two vectors are parallel then \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\]

 

• Projection of the joining of the two points on a line: If \[P({{x}_{1}},\,{{y}_{1}},\,{{z}_{1}})\] and \[Q({{x}_{2}},\,{{y}_{2}},\,{{z}_{2}})\] are two points, then the length of the projection of PQ on a line whose direction cosine are \[\ell \], m & n is written

as \[({{x}_{2}}-{{x}_{1}}).\ell +({{y}_{2}}-{{y}_{1}}).m+({{z}_{2}}-{{z}_{1}}).n\]

 

1. Find the projection of the line segment joining the points (1,1,2) and (3,4,1) on the line whose direction ratio be (2,3, 6)

 

Sol.      Here P= (1, 1, 2), Q= (3, 4, 1)

Given d.r. = (2, 3, 6)

1st of all we have to find the d.c.

                       

            \[\therefore \,\,\,\,\,\,\ell =\frac{2}{\sqrt{{{2}^{2}}+{{3}^{2}}+{{6}^{2}}}}=\frac{2}{7}\]

 

            \[m=\frac{3}{4}\] and \[n=\frac{6}{7}\]

\[\therefore \] Projection of the line joining the points (1, 1, 2) and (3, 4, 1) an the line whose d.c. be \[\left( \frac{2}{7},\frac{3}{7},\frac{6}{7} \right)\] is written as

            \[=(3-1)\times \frac{2}{7}+(4-1)\times \frac{3}{7}+(1-2)\times \frac{6}{7}=2\times \frac{2}{7}+3\times \frac{3}{7}+\frac{-6}{7}\]

 

            \[=\frac{4+9-6}{7}=\frac{7}{7}=1\]