Notes - Syllogism
Category : 11th Class
Learning Objectives
Introduction
“Syllogism” is a Greek word that means inference or deduction.
In ‘Reasoning’, syllogism is a kind of logical argument that applies deductive reasoning to arrive at a conclusion, based on two or more propositions that are asserted or assumed to be true.
The problems of syllogism is based on two parts:
(i) Proposition
(ii) Conclusion/conclusions drawn from given proposition/propositions.
Proposition
A proposition is the statement of a certain relation between two or more terms.
(a) The subject
(b) The predicate
In the proposition, “All novels are songs”, something is being said about ‘novels’. So ‘novel’ is the subject. ‘Song’ is the predicate here, because it affirms the statement about the subject.
Classification of Propositions
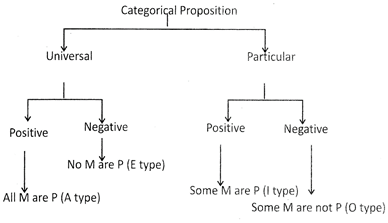
Universal Positive Proposition (a)
A proposition of the form "All S are P" is called a universal positive proposition. A universal positive proposition is denoted by A.
All girls are disciplined.
All snakes are reptiles.
Universal Negative Propositions (e)
A proposition of the form “No S is P” is called a universal negative proposition. It is denoted by E.
No professors are lazy.
No boys are intelligent.
No boxes are baskets.
Particular positive Proposition (I)
A proposition of the form "some S are P" is called a particular positive proposition. It is usually denoted by I.
Some boys are' smart.
Some men are foolish.
Some politicians are honest.
Particular Negative Proposition (O)
A proposition of the form "Same S are not P" is called particular negative proposition. It is denoted by O.
(i) Some flowers are not grapes.
(ii) Some animals are not wild.
(iii) Some students are not boys.
Hidden Proposition
You may find it difficult to categorise same propositions of the form –‘Rohit is brilliant’. 'Every small man speaks English'. 'Not a single student passed the annual exam', 'No student except Monika was present', etc.
We shall know how to find the hidden proposition in such sentences.
A-type Hidden Propositions
Every girl is beautiful.
[All girls are beautiful]
Each of them is healthy.
[All (of them) are healthy]
Any one could kill the lion.
[All can kill the lion]
Further, let us see the sentences given below:
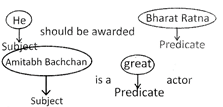
Thus, a positive sentence with a particular person as its subject is A type.
Also, a sentence in the following format is A type:
E - Type Hidden Proposition
No one (student) is studious.
[No student is studious]
None of the girl is beautiful.
[No girl is beautiful]
Not a single girl is healthy.
[No girl is healthy]
Further, let us see the sentences given below:


Thus, a negative sentence with a particular person on its subject is E type proposition. Also, sentences in following formats are E type: 
"Is there any truth left in the world"?
[No truth is left in the world.]
I -Type Hidden Proposition
Almost all the girls are beautiful.
[Some girls are beautiful]
Most of the garments are handmade.
[Some of the garments are handmade.]
Usually girls are beautiful.
[Some girls are beautiful]
A little money is left in my wallet.
[Some money is left in my wallet.]
Further, let us see the sentences given below:
Few girls are not studious.
[Some girls are studious.]
Rarely is a girl not beautiful.
[Some girls are beautiful]
Seldom are women not housewife.
[Some women are housewife.]
It is clear from the above given examples that negative sentences beginning with words like 'few', 'rarely', 'seldom', etc. (also 'hardly', 'scarcely', 'little' etc.) are to be deduced as I type.
Just see the other formats given below:
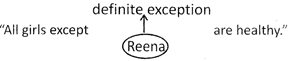
Not a definite exception as
name of girls are not given
All girls except ![]() are beautiful
are beautiful
[Some girls are beautiful]
Net a definite exception as
name of girls are not given
All girls except have passed.
[Some girls have passed]
Therefore, a positive proposition with an indefinite exception is deduced as I type.
O - Type Hidden Propositions
All girls are not beautiful.
[Some girls are not beautiful]
Every boy is not present.
[Some boys are not present]
Further, let us see the following sentences:
The poor are usually not healthy.
[Some poor are not healthy]
Almost all the girls are not beautiful.
[Some girls are not beautiful]
Most of the garments are not handmade.
[Some of the garments are not handmade]
Girls are not frequently short tempered.
[Some girls are not short tempered]
Now, it is clear from the above mentioned examples that negative propositions with words such as 'almost', 'frequently', 'most', 'mostly', 'a few', 'generally', etc. are to be reduced to the O type propositions.
Again positive propositions starting with words likes 'few', 'scarcely', 'rarely', 'little', 'seldom' etc. are said to be O type.
Seldom are women jealous.
[Some women are not jealous]
Few girls are beautiful.
[Some girls are beautiful]
Rarely is a wealthy person worried.
[Some wealthy persons not worried]
Also see the following formats:
Not a definite exception as
name of girls are not give n
No girls except ![]() are beautiful.
are beautiful.
[Some girls are not beautiful]
Nota a definite exception as
name of women are not given
No women except ![]() are housewife.
are housewife.
[Some women are not housewife] Therefore, a negative proposition with an indefinite exception, is reduced to O type.
Exclusive Propositions
A statement beginning with 'only', 'alone', 'none but’ or 'none else but’ is called exclusive proposition. Such propositions can be reduced to A or E or I type.
Only graduate are probationary officers.
\[\to \] No graduate are probationary officer. (E type)
\[\to \] All probationary officers are graduate. (A type)
\[\to \] Some graduates are probationary officers. (I type)
General format of sentences given in the examinations:
All M are P. (A type)
No M are P. (E type)
Some M are P. (I type)
Some M are not P. (O type)
Note: General formats given above are frequently asked formats in the examinations. But students must be ready for other hidden formats of A, E, I and O types of propositions as problems in hidden formats can also be given in question papers.
Conversion of Proposition
Two steps are to be followed in conversion. The first step is to change the subject as the predicate and the predicate as the subject. The second steps is to change the type of the given proposition to the pattern given in the following table.
Table of conversion
|
A |
------------- |
I |
|
E |
------------- |
E |
|
I |
------------- |
I |
|
O |
------------- |
Never get converted |
Conversion of A Type
Subject Predicate
![]()
after conversion it becomes
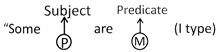
Therefore, it is clear that A type of propositions get converted into (type,
Conversion of E Type
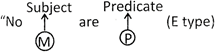
after conversion it becomes
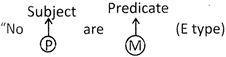
Therefore, E get converted into E.
Conversion of I Type

after conversion it becomes
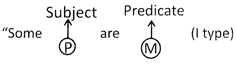
Therefore, I get converted into I.
Conversion of O Type
O type of proposition can't be converted.
Note: In each conversion, subject becomes predicate and predicate becomes subject.
Infect, conversion is an immediate inference that is drawn from two propositions and are called mediate inference.
Rule to Dram Conclusion
After knowing conversion of propositions, we must learn the rules to draw conclusions. In problems of syllogism, conclusions are drawn either from a single proposition or from two propositions. But a conclusion drawn from a single proposition is just a conversion of that proposition. While to get conclusion from two propositions a certain table is used that tells us what type of conclusion (form of proposition) we get out of two propositions. To understand it let us see the following conclusion table:
|
I Proposition |
II Proposition |
Conclusion |
|
A |
A |
A |
|
A |
E |
E |
|
E |
A |
(O) R |
|
E |
I |
(O) R |
|
I |
A |
I |
|
I |
E |
O |
|
Note (a) Apart from above 6 pairs of propositions, no other pair will give any conclusion. (b) The conclusion drawn out of two propositions is itself a proposition and its subject is the subject of the 1st statement while its predicate is the predicate of the 2nd statement. The common term gets disappeared. (c) (O) R does mean that the conclusion is 0 type but is in reverse order. In this case/the subject of the inference or conclusion is the predicate of the 2nd proposition and the predicate of the conclusion is the subject of the 1st sentence or statement. (d) The conclusion table gives correct conclusions or inference if and only the two propositions are aligned properly. |
What is Aligning
Let us see the following examples:
Example: 1
Statements:
I. All ![]() are beautiful.
are beautiful.
II. Some ![]() are Indian.
are Indian.
· Example: 2
Statements:
I. No ![]() is chair
is chair
II. Some tabes are ![]() .
.
Example: 3
Statements:
I. Some women are![]() .
.
II. No![]() is chair.
is chair.
In all the above mentioned examples, we notice that in two statements of every example, there is a common term. In example 1 the word 'girl' is common; in example 2 the word 'pen' is common; while in example 3 the word 'men7 is common.
Now, the aligning of the two statements (propositions) does mean that the pair of statements must be written in such a way that the common term is the predicate of the 1st sentence and the subject of the 2nd.
Just think over the following examples:
Statements:
I. Some girls are![]() .
.
II. All ![]() are tall.
are tall.
Hence, the common term 'cute' is the predicate of the I statement and subject of the 2nd statement. Therefore/ the two statements (I & II) are properly aligned.
But see another example
Statements:
I. Some ![]() are chairs.
are chairs.
II. Some cats are![]() .
.
Here, the sentences that are not aligned as the predicate of the 1st statement is not the subject of the 2nd.
Then how to align it? In such type of cases, we change the order of sentences. In another words we put I sentence in place of II and II in place of I:
II. Some cats are![]() .
.
I. Some ![]() are chairs.
are chairs.
Let us consider another pair of statements
I. All bats are chairs.
II. All bats are cats. Then how to align it? In fact, in such cases we do alignment in two ways:- (a) By converting statement I as:
I. Some chair are ![]()
II. All![]() are cats.
are cats.
And
(b) By changing the orders of the sentences and then converting the statement II:
Now 1st change the order as:
II. All bats are cats.
I. All bats are chairs.
Again we do conversion for II and the aligned pair takes the form as:
II. Some cats are ![]() .
.
I. All ![]() are chairs.
are chairs.
Therefore, as per the requirement and nature of the sentence the alignment is done:
(i) only by changing the order of sentences.
or
(ii) only by converting one of the sentences.
or
(iii) by changing the order of the statements then converting one of the sentences.
How to solve Problems?
This method has two main steps.
(a) Aligning the pair of sentences.
(b) Using conclusion table to draw conclusion.
Example:
Statements: I. All rats are cats.
When aligned it takes the form as
I. Some cats are![]() , [i type]
, [i type]
II. All![]() are men. [A type]
are men. [A type]
Now we use the conclusion table given in this chapter that says
I + A = I type of conclusion.
Therefore, the drawn conclusion must be:
"Some cats are men.? It is clear that the conclusion drawn "Some cats are men" is a mediate inference as it Is the result of two propositions. But in actual problem immediate inferences are also given in conclusion part and that format is given below:
Statement:
I. All rats are cats.
II. All rats are men.
Conclusion: (i) Some cats are men.
(ii) Some men are cats.
(iii) Some rats are cats.
(iv) Some cats are rats.
(v) Some rats are men.
(vi) Some men are rats.
Answer option:
(a) Only (iii) follows (b) Only (i), (ii), and (iii) follow
(c) Only (iv) follows (d) Only (i), (ii), (iv) and (vi)
(e) None of these
Here, the correct option is D.
Conclusion (i) follows because it is the mediate inference of statement I & II.
Conclusion (ii) is the conversion of conclusion (i).
Conclusion (iii) is the immediate inference (conversion) of statement I while
Conclusion (iv) is the conversion of conclusion (iii).
Conclusion (v) is the immediate inference (conversion) of statement II while
Conclusion (vi) is the conversion of conclusion (v).
Further, in some problems complementary pairs are also seen in the conclusion part in the forms of sentences given below:
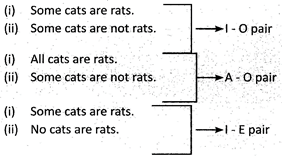
Apart from I-O, A-O and 1-E pair the two sentences must have same object and predicate as are the above mentioned pairs. For these pairs we write the form. Either (i) or (ii) follows.
For example, see the following format:
Statements: I. Some dogs are cats.
Conclusions: (i) Some cats are dogs.
(ii) Some rats are cats.
(iii) All cats are rats.
(iv) Some dogs are rats.
(v) Some dogs are not rats.
Ans. options: (a) All follow
(b) Only (i) follows
(c) Only (ii) and (iii) follow
(d) Either (iv) or (v) and (i) & (ii) follow
Here, option (d) is correct because conclusion (i) is the immediate inference (conversion) of statements I while conclusion (ii) is the immediate inference of II. Conclusion (iv) & (v) make complementary pair of I-O type. Conclusion (iii) is not correct because I and II are I type of statements and I + I does not give any conclusion. Further, A type of conclusion cannot be found from the immediate inference (conversion) of I type of statements, as I & II are.
|
Now, the complete process of solving syllogism problems can be summerised as below: (a) 1st step is aligning the sentence. (b) 2nd step is using conclusion table. (c) 3rd step is checking immediate inference & mediate inference. (d) 4th step is checking through the conversion of immediate inference & mediate inference. (e) Checking the complementary pairs. |
You need to login to perform this action.
You will be redirected in
3 sec
