12th Class Mathematics Applications of Derivatives Notes - Mathematics Olympiads -Application of Derivatives

 

                                                                                       Application of Derivatives

 

 

• Continuity and Differentiability of a function: Let a function \[y=f(x)\] is said to be continuous at

\[x=a\] then \[\underset{x\to {{a}^{-}}}{\mathop{\lim }}\,f(x)=\underset{x\to {{a}^{+}}}{\mathop{\lim }}\,\,\,f(x)=f(a)\]

Generally, a function is said to be continuous at \[x=a\] when the graph of that function can be drawn/sketched without lefting the pencil.

 

 

• Differentiation: The process of finding out the differentiability/derivatives of the function \[y=f(x)\]in the interval (a, b) is said to be differentiation.

 

• Derivatives of f(x): Let \[y=f(x)\] is continuous in interval [a, b]. Let a point \[c\in (a,b)\]

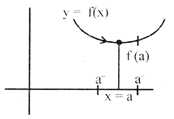
Then function \[y=f(x)\] is differentiable at \[x=c\]

i.e. \[\underset{x\to c}{\mathop{\lim }}\,\frac{f(x+c)-(c)}{c}=f'(c)\]

 

Solved Example

1. Find derivative of \[y=\sin x.\] by 1st principle:

Let \[y=f(x)=\sin x\]    ...(1)

Let \[\delta \]x be the small increment in x then \[\delta \]y be the corresponding increment in y.

\[y+\delta y=\sin (x+\delta x)\]   ...(2)

Now, on subtracting equation (1) from (2), we get

\[y+\delta y-y=\sin (x+\delta x)-\sin x\]

\[\delta y=2.\cos \frac{x+\delta x+x}{2}.\sin \left( \frac{x+\delta x+x}{2} \right)\]

Dividing \[\delta \]x on both sides and taking limit \[\delta x\to 0,\]we get

\[\underset{\delta x\to 0}{\mathop{\lim }}\,\frac{\delta y}{\delta x}=\underset{\delta x\to 0}{\mathop{\lim }}\,2.\frac{\cos \left( \frac{2x+\delta x}{2} \right).\sin \left( \frac{\delta x}{2} \right)}{\delta x}\]

\[\frac{dy}{dx}\underset{\delta x\to 0}{\mathop{\lim }}\,2.\cos \left( x+\frac{\delta x}{2} \right).\left( \frac{\sin \frac{\delta x}{2}}{\frac{\delta x}{2}\times 2} \right)\]

On applying limit \[\delta x\to 0,\]we get

\[\frac{dy}{dx}=\cos x\times 1=\cos x\left[ \underset{\theta \to 0}{\mathop{\lim }}\,\frac{\sin \theta }{\theta }=1 \right]\]

Thus,\[\frac{d}{dx}(\sin x)=\cos x\]

\[\frac{dy}{dx}\]is said to be differential coefficient of \[y=f(x).\] It is denoted by\[{{y}_{1}}\]or f \['(x)\]

 

• Some Important Formulae

1. \[\frac{d}{dx}(\sin x)=\cos x\]
2. \[\frac{d}{dx}(\cos x)=-\sin x\]
3. \[\frac{d}{dx}(\tan x)={{\sec }^{2}}x\]
4. \[\frac{d}{dx}(\cot x)=-\cos e{{c}^{2}}x\]
5. \[\frac{d}{dx}(\sec x)=\sec x\tan x\]
6. \[\frac{d}{dx}(\cos ec\,x)=-\cos ec\,x.\cot x\]
7. \[\frac{d}{dx}({{x}^{n}})=n{{x}^{n-1}}\]
8. \[\frac{d}{dx}({{e}^{x}})={{e}^{x}}\]
9. \[\frac{d}{dx}(\log x)=\frac{1}{x}\]
10. \[\frac{d}{dx}(si{{n}^{-1}}x)=\frac{1}{\sqrt{1-{{x}^{2}}}}\]
11. \[\frac{d}{dx}(co{{s}^{-1}}x)=\frac{-1}{\sqrt{1-{{x}^{2}}}}\]
12. \[\frac{d}{dx}(ta{{n}^{-1}}x)=\frac{1}{1+{{x}^{2}}}\]
13. \[\frac{d}{dx}(x)=1\]
14. \[\frac{d}{dx}(C)=0\] where \[C=\]any const.
15. \[\frac{d}{dx}(\sin ax)=a\,\text{cos}\,ax\]
16. \[\frac{d}{dx}({{a}^{x}})={{a}^{x}}.\log a\]

 

• Some Basic Rules of Differentiation

1. \[\frac{d}{dx}(u\,\pm v)=\frac{d}{dx}(u)\pm \frac{d}{dx}(v)\]where u and v be the function of x.
2. \[\frac{d}{dx}(C.u)=C.\frac{d}{dx}(u)\] where \[C=\]any const.

e.g. \[\frac{d}{dx}(5{{x}^{2}})=5.\frac{d}{dx}({{x}^{2}})=5[2.{{(x)}^{2-1}}]=10{{x}^{1}}=10x\]

3. \[\frac{d}{dx}(u.v.)=u.\frac{d\text{v}}{dx}+\frac{du}{dx}\]

e.g. \[\frac{d}{dx}({{e}^{x}}.\sin x)={{e}^{x}}.\frac{d}{dx}(\sin x)+\sin x\frac{d}{dx}({{e}^{x}})={{e}^{x}}\cos x+\sin x.{{e}^{x}}\]

\[={{e}^{x}}(\cos x+\sin x)\]

4. \[\frac{d}{dx}\left( \frac{u}{\text{v}} \right)=\frac{\text{v}.\frac{du}{dx}-u.\frac{d\text{v}}{dx}}{{{\text{v}}^{2}}}\] e.g. \[\frac{d}{dx}\left( \frac{{{x}^{2}}}{\sin x} \right)_{\text{v}}^{u}=\frac{\sin x\frac{d}{dx}({{x}^{2}})-{{x}^{2}}\frac{d}{dx}(\sin x)}{{{\sin }^{2}}x}\]
5. \[\frac{d}{dx}(lo{{g}_{c}}{{a}^{x}})=\frac{d}{dx({{a}^{x}})}(\log {{a}^{x}}).\frac{d}{dx}({{\underline{a}}^{x}})=\frac{1}{{{a}^{x}}}.{{a}^{x}}.\log a=\log a\]

 

• Tangent & Normals:

Geometrical meaning of derivative at point: The derivative of a function \[f(x)\] at a point \[x=a\] is the of the tangent of the curve \[y=f(x)\] at the point \[(a,f(a)).\]

 

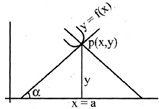
Let us consider a curve \[y=f(x)\] & take a point P\[(x,y)\] on it. We draw the tangent to the curve at \[P(x,y)\]which makes an angle \[\alpha \] with positive direction of x-axis. Then,

\[{{\left. \frac{dy}{dx} \right|}_{\,\,at\,\,P(x,y)\,=\,tan\,\,\alpha \,=\,m(say)}}\]

It is said to be gradient or slope of the tangent to the curve \[y=f(x)\]at\[p(x,y)\].

 

• Equation of the tangent: The equation of the tangent to a curve \[y=f(x)\] at the given point \[P({{x}_{1}},{{y}_{1}})\] is written in point slope form of the equation of straight line.

\[y-{{y}_{1}}=m(x-{{x}_{1}})\]

where m = slope of the tangent

\[y-{{y}_{1}}={{\left. \frac{-dy}{dx} \right|}_{\,\,at\,\,P({{x}_{1}},\,{{y}_{1}})\,\,\times \,\,(x-{{x}_{1}}).}}\]

 

• Equation of the Normal: The equation of the normal to the curve\[y=f(x)\] at the given point \[({{x}_{1}},{{y}_{1}})\] is written as

\[y-{{y}_{1}}=\frac{-1}{m}({{x}_{1}}-{{x}_{1}})\,\,y-{{y}_{1}}=\frac{-1}{{{\left. \frac{dy}{dx} \right|}_{\,\,at\,\,P({{x}_{1}},{{y}_{1}})}}}\times (x-{{x}_{1}})\]

Note: Since tangent & normal to a curve \[y=f(x)\] at point \[({{x}_{1}},{{y}_{1}})\] is perpendicular to each other at that point.

\[\because \,\,\,{{m}_{1}}.{{m}_{2}}=-1\]

Where, \[{{m}_{1}}=\] slope of the tangent to the curve

\[{{m}_{2}}=\] slope of the normal to the curve

 

Solved Examples

1. Find the equation of the tangent and normal to the curve \[y=2{{x}^{2}}+3\sin x,\]at \[x=0.\]

Sol. The given equation of the curve is

\[y=2{{x}^{2}}+3\sin x\]                               ....(1)

Putting\[x=0\]

then \[y=2\times 0+3\text{ }sin0=0.\]

Here, the point of the contact is (0, 0).

\[\because \] Differentiating (1) w.r.t. x, we get

\[\frac{dy}{dx}=2(2x)+3.\cos x{{\left. \frac{dy}{dx} \right|}_{\,\,at\,\,(0,0)}}=4\times 0+3cos({{0}^{\underline{o}}})=0+3=3\]

i.e. \[{{m}_{1}}=3\]

\[\therefore \] Equation of the tangent is

\[y-{{y}_{1}}=m(x-{{x}_{1}})\]

\[\Rightarrow y-0=3(x-0)\]

\[y=3x\Rightarrow 3x-y=0\]

Now, equation of the normal is

\[y-{{y}_{1}}=\frac{-1}{m}(x-{{x}_{1}})\]

\[\Rightarrow y-0=\frac{-1}{3}(x-0)\]

\[\Rightarrow 3y=-x\Rightarrow x+3y=0\]

 

• Some important points to remember:

1. If\[\frac{dy}{dx}>0,\] then the tangent to the curve makes an acute angle with the x-axis

 

2. If \[\frac{dy}{dx}<0,\] then the tangent to the curve makes an obtuse angle with the x-axis.
3. If \[\frac{dy}{dx}=0,\]then the tangent is parallel to the x-axis.
4. If \[\frac{dy}{dx}=\infty ,\]i.e., \[\frac{dy}{dx}=0,\] then tangent is perpendicular to the x-axis i.e.it is parallel to the y-axis.
5. If \[\frac{dy}{dx}=\pm 1\] i.e. \[\theta =45{}^\circ \]or \[135{}^\circ \], then the tangent is equally inclined to both the axis.
6. The slope of the line having the equation

\[ax+by+c=0\] is written as

\[m=\frac{-a}{b}=\frac{\text{coefficient of }x\text{ with negative sign}}{\text{coefficient of y}}\]

7. Two lines having slopes \[{{m}_{1}}\]and \[{{m}_{2}}\]are:

(a) perpendicular if \[{{m}_{1}}.{{m}_{2}}=-1\]

(b) parallel if \[{{m}_{1}}={{m}_{2}}\]

 

• Angle of intersection of two curves: Let \[y=f(x)\] & \[y=g(x)\] are two curves intersecting at point \[P(x,y).\] Then, the angle of intersection of two curves at point \[P(x,y)\] is equal to the angle between the tangent of the respective curves at that point of intersection \[P(x,y).\]

 

 

Let \[{{m}_{1}}=\] slope of the tangent to curve \[y=f(x)\] at \[P(x,y).\]

\[{{m}_{2}}=\] slope of the tangent to curve \[y=g(x)\] at \[P(x,y)\]

(In a triangle, sum of two interior angles is equal to an exterior angle.)

\[\therefore \,\,\,\,\alpha +\theta =\beta \]

So, \[\alpha \]be the angle of the tangent in the positive direction of x-axisa and \[\beta \] be the angle of the tangent to curve \[y=g(x)\] in the positive direction of x-axis.

\[\Rightarrow \theta =\beta -\alpha \Rightarrow \tan \theta =\tan (\beta -\alpha )=\frac{\tan \beta -\tan \alpha }{1+\tan \beta .\tan \alpha }\]

\[\Rightarrow \tan \theta =\frac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{2}}.{{m}_{1}}},\,\,\,\theta ={{\tan }^{-1}}\left| \left. \frac{{{m}_{2}}-{{m}_{1}}}{1+{{m}_{2}}.{{m}_{1}}} \right| \right.\]

 

• Length of Tangent/Normal/Sub-tangent& subnormal:

 

 

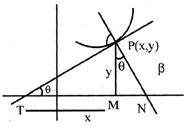
Let the tangent and normal on the point P(x, y) at the curve meet x-axis at T and N respectively. Let M be the foot of the ordinate at P. Then

In \[\Delta \text{PTM},\,\sin \theta =\frac{y}{\text{PT}}\Rightarrow PT=y\cos ec\,\theta \]

1. Length of the tangent \[=PT=\,\,|y.\cos ec\,\theta |\,\,=\left| \left. y.\sqrt{1+{{\cot }^{2}}\theta } \right| \right.\]

                        \[=y.\sqrt{1+\frac{1}{{{\left( \frac{dy}{dx} \right)}^{2}}}}=\frac{\sqrt[y]{1+{{\left( \frac{dy}{dx} \right)}^{2}}}}{\left( \frac{dy}{dx} \right)}\]

            Similarly,

Length of the normal \[=PN=y.\sec \theta =y.\sqrt{1+{{\tan }^{2}}\theta }=y\sqrt{1+{{\left( \frac{dy}{dx} \right)}^{2}}}\]

Length of the sub-tangent \[(TM)=y.cot\theta =\frac{y}{\tan \theta }=\frac{y}{\left( \frac{dy}{dx} \right)}\]

Length of the subnormal \[(MN)=y.\tan \theta =\left| \left. y.\frac{dy}{dx} \right| \right.\]

 

Solved Examples

1. A man 2 metre high walks at uniform speed of 6 metre per minute away from the lamp post of height 5 metre. Find the rate at which the length of his shadow increase.

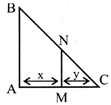
Sol. Let AB is a lamp post. At any instant t, A man MN away x m from AB and its shadow is y metre. Given that

\[AB=5m\]

\[MN=2m\] and \[\frac{dx}{dt}=6\]metre / min

\[AM=x\]metre and \[MC=y\] metre.

Since, \[\Delta ABC\] and \[\Delta MNC\] be similar

So, \[\frac{MN}{AB}=\frac{MC}{AC}\]      \[\Rightarrow \,\,\,\,\frac{AB}{MN}=\frac{AC}{MC}\]

\[\Rightarrow \,\,\,\,\frac{5}{2}=\frac{x+y}{y}\]       \[\Rightarrow \,\,\,\,\frac{5}{2}=1+\frac{x}{y}\]

\[\Rightarrow \,\,\,\,\frac{5}{2}-1=\frac{x}{y}\]      \[\Rightarrow \,\,\,\,\frac{3}{2}=\frac{x}{y}\,\,\,\,\Rightarrow 3y=2x\]

Differentiating w.r.t. to t, we get

\[3.\frac{dy}{dt}=2\left( \frac{dx}{dt} \right)\]        \[\Rightarrow \,\,\,\,\frac{dy}{dt}=\frac{2}{3}\times 6=4\]m/sec

 

2. Use differentiation to find the approximate value of \[\sqrt{0.037}.\]

Sol. Let \[y=f(x)=\sqrt{x}\]

Let \[x=0.040\] and \[x+\delta x=0.037\]

\[\delta x=x+\delta x-x=0.037-0.040=-0.003\]

For

\[\because y=f(x)=\sqrt{0.04}=0.2\]

\[\therefore dy=\left( \frac{\delta y}{\delta x} \right).dx\]

\[\therefore \frac{dy}{dx}=\frac{\delta }{\delta x}(\sqrt{x})=\frac{1}{2\sqrt{x}}\le \]

\[{{\left. \frac{dy}{dx} \right|}_{\,\,at\,\,x=0.04}}=\frac{1}{2\sqrt{x}}=\frac{1}{2\times 0.2}=\frac{1}{0.4}\]

So, \[\delta y={{\left( \frac{\delta y}{\delta x} \right)}_{at\,\,x=0.04}}\times \delta x=\frac{1}{0.4}\times (-0.003)=-\frac{3}{400}\]

\[\therefore \] Approximate value of \[y=f(x)=y+\delta y=0.2+\left( \frac{-3}{400} \right)=\frac{80-3}{400}=\frac{77}{400}\]

 

• Increasing & decreasing function (monotonic function): A function is said to be monotonic function if it is either increasing or decreasing.

 

• Increasing function:

(i)   A function \[y=f(x)\] is said to be increasing on an interval \[[a,b]\]if\[{{x}_{1}}<{{x}_{2}}\]in\[(a,b)\]\[\Rightarrow f({{x}_{1}})\le f({{x}_{2}})\]\[\forall \,{{x}_{1}},{{x}_{2}}\in (a,b)\]

(ii) A function \[y=f(x)\] is said to be strictly increasing on\[(a,b)\]if\[{{x}_{1}}<{{x}_{2}}\]in\[(a,b)\]\[\Rightarrow f({{x}_{1}})<f({{x}_{2}})\] for all \[{{x}_{1}},{{x}_{2}}\in (a,b)\]

 

• Decreasing function:

(i) A function \[y=f(x)\] is said to be decreasing on the interval\[(a,b)\] if \[{{x}_{1}}>{{x}_{2}}\]in\[(a,b)\]\[\Rightarrow f({{x}_{1}})\ge f({{x}_{2}})\]\[\forall \,{{x}_{1}},{{x}_{2}}\in (a,b)\]

(ii) A f unction\[y=f(x)\] is said to be strictly decreasing on \[(a,b)\] if\[{{x}_{1}}>{{x}_{2}}\]in\[(a,b)\]\[\Rightarrow f({{x}_{1}})>f({{x}_{2}})\]\[\forall \,{{x}_{1}},{{x}_{2}}\in (a,b)\]

 

• Test of monotonicity of function:

(i)  \[f(x)\] is increasing in \[[a,b]\] if \[f'(x)\ge 0\]\[\forall x\in [a,b]\]

(ii) \[f(x)\] is strictly increasing in \[[a,b]\]if \[f'(x)>0\]\[\forall x\in [a,b]\]

(iii) \[f(x)\] is decreasing in \[[a,b]\] if \[f'(x)\le 0\]\[\forall x\in [a,b]\]

(iv) \[f(x)\] is strictly decreasing in \[[a,b]\]if \[f'(x)<0\]\[\forall x\in [a,b]\]