Notes - Mathematics Olympiads -Integral Calculus
Category : 12th Class
Integral Calculus
Integration is the inverse process of differentiation i.e. the process of finding out the integral of the integrand function is called integration.
e.g. If \[\frac{d}{dx}\{F(x)\}=f(x),\]then\[\int{f(x).dx=F(x)+C}\]
Here function f(x) is said to be integrand and value of\[\int{f(x).dx=F(x)}\] is said to be integral value the function, \[c=\] Integration constant
|
Derivatives |
Integrals: |
|
|
1. |
\[\frac{d}{dx}({{x}^{n}})=n.{{x}^{n-1}}\] |
\[\int{{{x}^{n}}.dx=\frac{{{x}^{n}}+1}{n+1}+c}\] where \[c=\]integration constant. |
|
2. |
\[\frac{d}{dx}({{e}^{x}})={{e}^{x}}\] |
\[\int{{{e}^{x}}.dx={{e}^{x}}+c}\] |
|
3. |
\[\frac{d}{dx}\{\log (x)\}=\frac{1}{x}\] |
\[\int{\frac{1}{x}.dx=\log x+c}\] |
|
4. |
\[\frac{d}{dx}({{a}^{x}})={{a}^{x}}.\log a\] |
\[\int{{{a}^{x}}.dx=\frac{{{a}^{x}}}{\log a}+c}\] |
|
5. |
\[\frac{d}{dx}(\sin x)=\cos x\] |
\[\int{\cos x.dx=\sin x+c}\] |
|
6. |
\[\frac{d}{dx}(cosx)=-\sin x\] |
\[\int{\sin xdx=-\cos x+c}\] |
|
7. |
\[\frac{d}{dx}(tanx)={{\sec }^{2}}x\] |
\[\int{{{\sec }^{2}}xdx=\tan x+c}\] |
|
8. |
\[\frac{d}{dx}(cotx)=-\cos e{{c}^{2}}x\] |
\[\int{\cos e{{c}^{2}}xdx=-\cot x+c}\] |
|
9. |
\[\frac{d}{dx}(secx)=\sec x.\tan x\] |
\[\int{\sec x.\tan x.dx=\sec x+c}\] |
|
10. |
\[\frac{d}{dx}(cosecx)=-\cos ecx.\cot x\] |
\[\int{\cos ecx.cotx.dx=-\cos ec\,x+c}\] |
|
11. |
\[\frac{d}{dx}(ta{{n}^{-1}}x)=\frac{1}{1+{{x}^{2}}}\] |
\[\int{\frac{1}{1+{{x}^{2}}}.dx={{\tan }^{-1}}x+c}\] |
|
12. |
\[\frac{d}{dx}(si{{n}^{-1}}x)=\frac{1}{\sqrt{1-{{x}^{2}}}}\] |
\[\int{\frac{1}{\sqrt{1-{{x}^{2}}}}.dx={{\sin }^{-1}}x+c}\] |
|
13. |
\[\frac{d}{dx}(co{{s}^{-1}}x)=\frac{-1}{\sqrt{1-{{x}^{2}}}};\] |
\[\int{\frac{1}{\sqrt{1-{{x}^{2}}}}=-{{\cos }^{-1}}x+c}\] |
|
14. |
\[\frac{d}{dx}(ta{{n}^{-1}}x)=\frac{1}{1+{{x}^{2}}};\] |
\[\int{\frac{dx}{1+{{x}^{2}}}={{\tan }^{-1}}x+c}\] |
|
15. |
\[\frac{d}{dx}(-co{{t}^{-1}}x)=\frac{1}{1+{{x}^{2}}};\] |
\[\int{\frac{1}{1+{{x}^{2}}}dx=-{{\cot }^{-1}}x+c}\] |
|
16. |
\[\frac{d}{dx}(se{{c}^{-1}}x)=\frac{1}{x\sqrt{{{x}^{2}}-1}};\] |
\[\int{\frac{1}{x\sqrt{{{x}^{2}}-1}}.dx={{\sec }^{-1}}x+c}\] |
|
17. |
\[\frac{d}{dx}(-cose{{c}^{-1}}x)=\frac{1}{x\sqrt{{{x}^{2}}-1}};\] |
\[\int{\frac{dx}{x\sqrt{{{x}^{2}}-1}}=-\cos e{{c}^{-1}}x+c}\] |
By substituting \[x=g(t).\]
\[\because \] Let us consider, \[I=\int{f(x).dx}\]
Putting \[x=g(t)\]then\[dx=g'(t).dt\]\[\Rightarrow I=\int{f\{g(t)\}.g'(t).dt}\]
This change of variable formula is one of the important tools available to us for integrating various functions.
Sol. Let
\[I=\int{{{e}^{x}}(\tan x+\sec x+\sec x.\tan x+{{\sec }^{2}}x}).dx\]
Putting\[f(x)=\tan x+\sec x,\]we get
\[f'(x)={{\sec }^{2}}x+\sec x.\tan x\]
\[\therefore I=\int{{{e}^{x}}\{f(x)+f'(x)}\}dx={{e}^{x}}.f(x)+c={{e}^{x}}(\tan x+\sec x)+c\]
Check the degree of \[p(x)\] & \[q(x).\]
If the degree of \[p(x)>\] degree of \[q(x),\] then divide the \[p(x)\] by \[g(x)\] till its degree becomes less than the degree of \[g(x).\]
i.e. put in the form
\[\frac{p(x)}{q(x)}=r(x)+\frac{f(x)}{g(x)}\]
where degree of \[f(x)<\] degree of \[g(x)\]
Case-I: When the denominator contains non-repeated linear factors i.e., \[g(x)=(x-{{a}_{1}})(x-{{a}_{2}})......(x-{{a}_{n}})\]
Then\[\frac{f(x)}{g(x)}\]can be written as
\[\frac{f(x)}{g(x)}=\frac{{{A}_{1}}}{(x-{{a}_{1}})}+\frac{{{A}_{2}}}{(x-{{a}_{2}})}+.......+\frac{{{A}_{n}}}{(x-{{a}_{n}})}\]
Where\[{{A}_{1}}{{A}_{2}}.....{{A}_{n}}\] are constant to be determined by comparing the coefficient of various power of x on both side & taking L.C.M.
e.g. Let u & v be two function of x.
Then \[\int{u.\text{v}.dx=u\int \text{v}\text{.}dx-\int \left[ \frac{du}{dx}.\int \text{v}.dx \right]}dx\]
i.e. integration of product of two functions= 1st function \[\times \] integral of 2nd function \[-\] integral of product of differentiation of 1st & integral of 2nd function.
For applying this formula, we may have to decide which function should be 1st & 2nd function. Keep remember the following tips and you will have no difficulties to choose the 1st & 2nd function.
To choose the 1st function use I LATE formula:
I for inverse function
L for Logarithmic function
A for Algebraic function
T for Trigonometric function
E for Exponential function
It means if we have two functions from which one is inverse trigonometric and other is logarithmic, then inverse trigonometric function will be the first function.
Solved Example
Sol. Let \[I=\int{x.{{e}^{x}}.dx.}\]
Using ILate
A come first before E.
So, x will be the first function because it is algebric function & \[{{e}^{x}}\] be 2nd function because it is exponential term.
Now, \[I=\int{x.{{e}^{x}}.dx.}\]
\[=x.\int {{e}^{x}}.dx-\int \left\{ \left[ \frac{d}{dx}(x) \right].\int {{e}^{x}}.dx \right\}.dx=x.{{e}^{x}}-\int{1.{{e}^{x}}.dx=x.}\]\[{{e}^{x}}-{{e}^{x}}+c\]
\[={{e}^{x}}(x-1)+c\]
\[=\frac{1}{2}\int{\frac{\sin x+\cos x+(\cos x-\sin x)}{(\sin x+\cos x)}.dx}\]
Where \[f(x)=\sin x+\cos x=\frac{1}{2}[x+\log (\sin x+\cos x)]+c\]
Now, putting \[{{x}^{2}}=z.\]
\[\therefore dz=2x.dx\]
\[I=\frac{1}{2}\int{\frac{dz}{{{e}^{z}}}=\frac{1}{2}\int{{{e}^{-z}}.dz=\frac{-{{e}^{-z}}}{2}+c}=\frac{-1}{2.{{e}^{+z}}}+c=\frac{-1}{2.{{e}^{x}}^{^{2}}}}+c\]
\left. (x+\sqrt{{{x}^{2}}-{{a}^{2}}}) \right| \\
\end{matrix} \right.+c\]
\left. (x+\sqrt{{{x}^{2}}+{{a}^{2}}}) \right| \\
\end{matrix} \right.+c\]
\[\int{\frac{dx}{a+b\cos x}}\]or \[\int{\frac{dx}{a+b\sin x}}\]or \[\int{\frac{dx}{a\cos x+b\sin x+c}}\]
Step 1. Put\[\cos x=\frac{1-{{\tan }^{2}}\frac{x}{2}}{1+{{\tan }^{2}}\frac{x}{2}}\]and \[\sin x=\frac{2\tan \frac{x}{2}}{1+{{\tan }^{2}}\frac{x}{2}}\]
Step 2. Then put\[\tan \frac{x}{2}=t\]\[\Rightarrow dt=\frac{1}{2}{{\sec }^{2}}\frac{x}{2}.dx.\]After finding the integral in the form of t, convert t into x, putting \[t=\tan \frac{x}{2}.\]Other technique can be adopted as:
where \[{{x}^{2}}+bx+c\] cannot be factorised further.
\[\int{\frac{dx}{a+b{{\cos }^{2}}x}}\]or \[\int{\frac{dx}{a+b{{\sin }^{2}}x}}\]or \[\int{\frac{dx}{a{{\cos }^{2}}x+b{{\sin }^{2}}x+c.\sin x.\cos x}}\]
Step 1. Divide the numerator & denominator by \[{{\cos }^{2}}x.\]
Step 2. Replace \[{{\sec }^{2}}x\] by \[1+{{\tan }^{2}}x\] in denominator.
Step 3. Then put\[\tan x=t\]to get \[dt={{\sec }^{2}}x.dx.\]
Then integrate the function in form oft. After finding out the integral in t, convert t into x by putting \[t=\tan x.\]
Solved Example
Sol. Let \[I=\int{\frac{dx}{1-{{\cos }^{4}}x}}\]
Dividing numerator and denominator by\[{{\cos }^{2}}x,\]we have
\[\int{\frac{\frac{1}{{{\cos }^{2}}x}}{\frac{1}{{{\cos }^{2}}x}-\frac{{{\cos }^{4}}x}{{{\cos }^{2}}x}}.dx=\int{\frac{{{\sec }^{2}}x}{{{\sec }^{2}}x-co{{x}^{2}}x}.dx=\int{\frac{{{\sec }^{2}}x}{{{\sec }^{2}}x-\frac{1}{{{\sec }^{2}}x}}.dx}}}\]
\[=\int{\frac{{{\sec }^{2}}x}{(1+{{\tan }^{2}}x)-\frac{1}{(1+{{\tan }^{2}}x)}}.dx}\]
Putting\[\tan x=t\Rightarrow dt={{\sec }^{2}}x.dx\]
Now, \[I=\int{\frac{dt}{(1+{{t}^{2}})-\frac{1}{(1+{{t}^{2}})}}=\int{\frac{(1+{{t}^{2}})dt}{{{t}^{2}}({{t}^{2}}+2)}=\int{\frac{{{t}^{2}}}{{{t}^{2}}({{t}^{2}}+2)}dt+\int{\frac{1}{{{t}^{2}}({{t}^{2}}+2)}dt}}}}\]
\[=\int{\frac{1}{{{t}^{2}}+2)}dt+\int{\frac{1}{{{t}^{2}}({{t}^{2}}+2)}dt}}\]
Let \[(I)={{I}_{1}}+{{I}_{2}}\](say)
Now, \[{{I}_{1}}=\int{\frac{I}{({{t}^{2}}+2)}}dt=\frac{1}{\sqrt{2}}{{\tan }^{-1}}\left( \frac{t}{\sqrt{2}} \right)\] and \[{{I}_{2}}=\int{\frac{1}{{{t}^{2}}({{t}^{2}}+2)}dt}\]
To solve the \[{{I}_{2}},\] let \[\frac{1}{{{t}^{2}}({{t}^{2}}+2)}=\frac{A}{{{t}^{2}}}+\frac{B}{{{t}^{2}}+2}\]
\[\frac{1}{{{t}^{2}}(t+2)}=\frac{A{{t}^{2}}+2A+B{{t}^{2}}}{{{t}^{2}}({{t}^{2}}+2)}\]
On comparing the coefficients, we get
\[A+B=0\]and\[2A=1\]
\[\Rightarrow A=\frac{1}{2},\] \[B=\frac{-1}{2}\]
So \[{{I}_{2}}=\int{\left[ \frac{1}{2{{t}^{2}}}-\frac{1}{2({{t}^{2}}+2} \right]}dt=\int{\frac{1}{2{{t}^{2}}}dt-\frac{1}{2}\int{\frac{1}{{{t}^{2}}+2}dt}}\]
\[=\left( \frac{1}{2} \right)\frac{{{t}^{-1}}}{(-1)}-\frac{1}{2}\left[ \frac{t}{\sqrt{2}}{{\tan }^{-1}}\left( \frac{t}{\sqrt{2}} \right) \right]+C=\frac{-1}{2t}-\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\frac{t}{\sqrt{2}}+C\]
So, \[I={{I}_{1}}+{{I}_{2}}=\frac{1}{\sqrt{2}}{{\tan }^{-1}}\left( \frac{t}{\sqrt{2}} \right)+\frac{-1}{2t}-\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\frac{t}{\sqrt{2}}+C\]
\[=\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\left( \frac{t}{\sqrt{2}} \right)-\frac{1}{2t}+C=\frac{1}{2\sqrt{2}}{{\tan }^{-1}}\left( \frac{\tan x}{\sqrt{2}} \right)\frac{1}{2\tan x}+C\]
To choose\[t=\sin x\]or\[\cos x\]. You are independent, but you will have to adopt one of that tool either \[t=\sin x\]or\[t=\cos x\]. By substituting the function in the other variable. Otherwise use the reduction formulae.
or \[\int{(\alpha x+\beta ).\sqrt{a{{x}^{2}}+bx+c}}.dx\]
When \[f(x)=\frac{\alpha x+\beta }{a{{x}^{2}}+bx+c}\]
Putting \[\alpha x+\beta =\lambda \](differentiation of denominator)\[+m=\lambda (2ax+b)+m\]
Then comparing the coefficient of x & const. term on both sides, we have find the integral after substituting the constant term \[\lambda \]& m.
Step 1. Dividing numerator & denominator by \[{{x}^{2}}\]
Step 2. Then put\[x+\frac{1}{x}=t\]or\[x-\frac{1}{x}=t\]
Whichever substitution, on differentiation gives the numerator of resulting integrand.
Step 3. Evaluate the resulting integral in terms of z and then express the result in the terms of x.
Solved Example
Sol. Let\[I=\int{\frac{{{x}^{2}}+1}{{{x}^{4}}+1}.dx}\]
On dividing numerator & denominator by\[{{x}^{2}}\], we get
\[\therefore \,\,\,\,\,\,I=\int{\frac{{{x}^{2}}+\frac{1}{{{x}^{2}}}}{\frac{{{x}^{4}}+1}{{{x}^{2}}}}}.dx\]
\[\therefore \,\,\,\,\,\,I=\int{\frac{1+\frac{1}{{{x}^{2}}}}{{{x}^{2}}+\frac{1}{{{x}^{2}}}}}.dx=\int{\frac{1+\frac{1}{{{x}^{2}}}}{({{x}^{2}})+{{\left( \frac{1}{x} \right)}^{2}}}.dx=\int{\frac{1+\frac{1}{{{x}^{2}}}}{{{\left( x-\frac{1}{x} \right)}^{2}}+2}.dx}}\]
Now put \[x-\frac{1}{x}=t\]\[\Rightarrow dt=\left( 1+\frac{1}{{{x}^{2}}} \right).dx\]
\[\therefore \,\,\,\,\,\,I=\int{\frac{dt}{{{t}^{2}}+2}=\int{\frac{dt}{{{t}^{2}}+{{(\sqrt{2})}^{2}}}}}\]\[=\frac{1}{\sqrt{2}}.{{\tan }^{-1}}\left( \frac{t}{\sqrt{2}} \right)+c\]
\[=\frac{1}{\sqrt{2}}.{{\tan }^{-1}}\frac{\left( x-\frac{1}{x} \right)}{\sqrt{2}}+c=\frac{1}{\sqrt{2}}{{\tan }^{-1}}\left( \frac{{{x}^{2}}-1}{\sqrt{2}x} \right)+c\]
\[\int_{a}^{b}{f(x).dx=[F(x)]_{a}^{b}}=F(b)-F(a)\]
e.g. \[I=\int_{0}^{4}{(x+{{e}^{2x}}).dx}\]
\[\therefore \,\,\,\,\,\,I=\int_{0}^{4}{(x+{{e}^{2x}}).dx}=\frac{{{x}^{2}}}{2}+\frac{{{e}^{2x}}}{2}\]
\[\therefore \,\,\,\,\,\,I=\int\limits_{0}^{4}{(x+{{e}^{2x}}).dx}=\left( \frac{{{x}^{2}}}{2}-\frac{{{e}^{2x}}}{2} \right)_{0}^{4}=\frac{({{4}^{2}}-{{0}^{2}})-({{e}^{2\times 4}}-{{e}^{2\times 0}})}{2}\]
\[=\frac{4\times 4-{{e}^{8}}+1}{2}=\frac{17-{{e}^{8}}}{2}\]
(ii) \[\int\limits_{-a}^{a}{f(x)dx=0,}\]when\[f(x)\]is odd function i.e.\[f(-x)=-f(x)\]
(ii) \[\int\limits_{0}^{2a}{f(x)dx=}0\]; If \[f(2a-x)=-f(x)\]
Solved Example
Sol. On putting \[x={{\cos }^{2}}\theta ,\]\[dx=-2\cos \theta .\sin \theta \,d\,\theta .\]
Now\[I=\int{\sqrt{\frac{1-\cos \theta }{1+\cos \theta }}}(-2\sin \theta .\cos \theta ).d\theta \]
\[=\int{\tan \frac{\theta }{2}(-2).\cos \theta .2\sin \frac{\theta }{2}.cos\frac{\theta }{2}.d\theta }\]\[=-4\int{\frac{\sin \frac{\theta }{2}}{\cos \frac{\theta }{2}}.\cos \theta .\sin \frac{\theta }{2}.\cos \frac{\theta }{2}.d\theta }\]
\[=4\int{\cos }\theta .{{\sin }^{2}}\frac{\theta }{2}.d\theta =4\int{\left( 1-2{{\sin }^{2}}\frac{\theta }{2} \right)}.{{\sin }^{2}}\frac{\theta }{2}.d\theta \]
\[=4\int{\left( {{\sin }^{2}}\frac{\theta }{2}-2{{\sin }^{4}}\frac{\theta }{2} \right).d\theta =4\left[ \int{{{\sin }^{2}}\frac{\theta }{2}.d\theta -8}\int{{{\sin }^{4}}\frac{\theta }{2}.d\theta } \right]}\]
\[=4\int{\left( \frac{1-\cos \theta }{2} \right)}d\theta -8\int{{{\left( \frac{1-\cos \theta }{2} \right)}^{2}}d\theta }\]
\[=4\left( \frac{1}{2}\theta -\frac{\sin \theta }{2} \right)-8\left[ \int{\frac{1+{{\cos }^{2}}\theta -2\cos \theta }{4}}d\theta \right]\]
\[=2\left( \theta -\sin \theta \right)-8\left[ \int{\left( \frac{1}{4}+\frac{1+\cos 2\theta }{8}-\frac{\cos \theta }{2} \right).}d\theta \right]\]
\[=2\theta -2\sin \theta -2\theta -\theta -\frac{\sin 2\theta }{2}+4\sin \theta =-\theta +2\sin \theta -\sin \theta \cos \theta \]
\[=-{{\cos }^{-1}}\sqrt{x}+2\sqrt{1-x}-\sqrt{x}\sqrt{1-x}+c\]
\[\therefore {{\text{I}}_{n}}=\int\limits_{0}^{\frac{\pi }{2}}{{{\sin }^{n}}x.dx=\left\{ \frac{(n-1)(n-3)(n-5)....6.4.2}{n(n-2)(n-4)....7.5.3.1} \right\}}\]when n is odd
\[{{\text{I}}_{n}}=\int\limits_{0}^{\frac{\pi }{2}}{{{\cos }^{n}}x.dx=}\left\{ \frac{(n-1)(n-3)(n-5)....5.3.1}{n(n-2)(n-4)....6.4.2}\times \frac{\pi }{2} \right.\]
When n is even
\[{{\text{I}}_{n}}=\int\limits_{0}^{\frac{\pi }{4}}{{{\tan }^{n}}x.dx}=\frac{1}{n-1}-{{\text{I}}_{n-2}}\,\,{{\text{I}}_{n}}\text{+}{{\text{I}}_{n-2}}=\frac{1}{n-1}\]
\[{{\text{I}}_{n}}=\int{{{\sec }^{n}}xdx=\frac{\tan x.{{\sec }^{n-2}}x}{n-1}+\frac{n-2}{n-1}.}{{\text{I}}_{n-2}}\]
\[\int\limits_{0}^{\pi /4}{{{\sec }^{n}}x.dx}=\frac{{{(\sqrt{2})}^{n-2}}-1}{n-1}+\left( \frac{n-2}{n-1} \right).{{\text{I}}_{n-2}}\]
\[{{\text{I}}_{n}}=\frac{{{x}^{n}}{{e}^{ax}}}{a}-\frac{n}{a}.{{I}_{n-1}}\]
\[=\frac{{{\sin }^{m+1}}x.{{\cos }^{n-1}}x}{m+n}+\frac{n-1}{m+n}.\int{{{\sin }^{m}}x.{{\cos }^{n-2}}x\,dx}\]
(ii) \[\int{{{\sin }^{m}}x.co{{s}^{n}}xdx}=-\frac{{{\sin }^{m-1}}x{{\cos }^{n+1}}x}{m+n}+\frac{m-1}{m+n}\int{{{\sin }^{m-2}}x.co{{s}^{n}}x\,dx}\]
(ii) \[\int\limits_{0}^{\pi /2}{{{\sin }^{m}}x.{{\cos }^{n}}xdx}=\frac{m-1}{m+n}\,\,\int\limits_{0}^{\pi /2}{si{{m}^{m-2}}x{{\cos }^{n}}xdx}\]
(a) \[\int\limits_{a}^{ma}{f(x).dx}=m\int\limits_{0}^{a}{f(x).dx}\]
(b) \[\int\limits_{a}^{m.a}{f(x).dx}=(m-1).\int\limits_{0}^{a}{f(x).dx}\]
(c) \[\int\limits_{ma}^{m(a+b)}{f(x).dx}=\int\limits_{a}^{b}{f(x).dx}\](cancelled same term in the limit)
(d) \[\int\limits_{b}^{na+b}{f(x).dx}=0\](result independent of b)
\[I=\int\limits_{a}^{b}{\left| \left. f(x) \right| \right.}.dx\]
First of all, solve the equation\[f(x)=0\]
Suppose value of\[x=\alpha \And \beta \]etc.
Then, partition the given limits such that i.e. \[(a<\alpha <\beta <b).\]
\[(a,\alpha ),(\alpha ,\beta ),(\beta ,b)\]etc.
Check the sign of \[f(x)\] by taking any point in each of these intervals
Lastly use the properties of integral.
\[\int\limits_{a}^{b}{f(x).dx=\int\limits_{a}^{\alpha }{f(x).dx}+\int\limits_{\alpha }^{\beta }{f(x).dx}+\int\limits_{\beta }^{b}{f(x).dx.}}\] e.g. \[I=\int\limits_{2}^{8}{\left| \left. x-5 \right| \right..dx}\]
\[\because \,\,\,\,\,f(x)=x-5=0\Rightarrow x=5\]
\[\because \,\,\,\,\,\int\limits_{2}^{5}{f(x).dx+\int\limits_{5}^{8}{f(x).dx=\int\limits_{2}^{5}{-(x-5)dx+\int\limits_{5}^{8}{(x+5).dx}}}}\]
\[=\left( -\frac{{{x}^{2}}}{2}+5x \right)_{2}^{5}+\left( \frac{{{x}^{2}}}{2}+5x \right)_{5}^{8}\]
\[=\left( \frac{-25}{2}+25 \right)-\left( \frac{-4}{2}+10 \right)+\left( \frac{64}{2}+40 \right)-\left( \frac{25}{2}+25 \right)\]\[=\frac{25}{2}-8+72-\frac{75}{2}\]
\[=\frac{-50}{2}+64=-25+64=39\]
Area of Plane Region:
\[A=\int\limits_{a}^{b}{y\,dx}=\int\limits_{a}^{b}{f(x)dx}\]
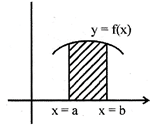
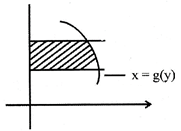
2. The area bounded by the curve \[x=g(x),\]y-axis\[y=c\]&\[y=d(d>c)\]is given by
\[A=\int\limits_{c}^{d}{xdy}=\int\limits_{c}^{d}{g(y)dy}\]
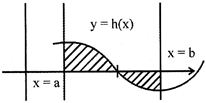
3. The area bounded by the curve\[y=h(x)\](which intersects the x-axis as shown below), x-axis & the two ordinate \[x=a\]and \[x=b\]is written as
![]()
If the two curves\[y=f(x)\]&\[y=g(x).\]Such that \[y=f(x)\]lies above the curve\[y=g(x)\]& both are the above the x-axis then bounded by them and the ordinate\[x=a\]& \[x=b\]\[(b>a)\]is written as
\[A=\int\limits_{a}^{b}{f(x).dx}-\int\limits_{a}^{b}{g(x).dx}\]
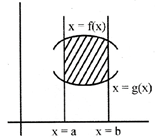
i.e. A=upper curve\[-\]lower curve
The area bounded by the curves \[y=f(x)\]& \[y=g(x)\](which intersect each other as shown in the figure) between the of ordinates\[x=a\] and\[x=b\]is written as
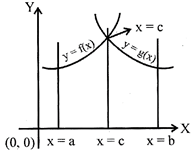
\[A=\int\limits_{a}^{c}{f(x).dx+\int\limits_{c}^{b}{g(x).dx}}\]where\[c=\]point of intersection of two curves.
You need to login to perform this action.
You will be redirected in
3 sec
