Notes - Mathematics Olympiads -Matrices and Determinats
Category : 12th Class
Matrices and Determinants
\[{{a}_{1}}x+{{b}_{1}}y={{c}_{1}}\] (i)
\[{{a}_{2}}x+{{b}_{2}}y={{c}_{2}}\] (ii)
We have one of the methods to solve these equation by cross multiplication method.
\[\frac{x}{{{b}_{1}}{{c}_{2}}-{{b}_{2}}{{c}_{1}}}=\frac{y}{{{c}_{1}}{{a}_{2}}-{{c}_{2}}{{a}_{1}}}=\frac{1}{{{a}_{1}}{{b}_{2}}-{{a}_{2}}{{b}_{1}}}\]
Now, we learn to solve such equations with the help of matrices and determinants.
Given linear equation can be solved by matrix method & it is written as,
AX = B
Where
![]()
Generally, it is represented as, where \[A=[{{a}_{ij}}]\]
i = 1, 2, 3, ........ m
j = 1, 2, 3, ....... n.
Here subscript i denotes no. of rows.
& subscript j determines no. of columns.
& \[{{a}_{ij}}\to \] represent the position of element a in the given matrix
e.g \[A=[{{a}_{ij}}]\] & if
![]()
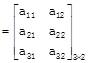
In the above example
Order of matrix \[A=3\times 2\] in which 3 determine no. of row & 2 determine no. of column of given matrix.
(a) Addition of matrices
(b) Subtraction of matrix
(c) Multiplication of matrix
(d) Adjoint of matrix
(e) Inverse of matrixes.
![]()
![]()
Note: For addition or substraction operation of two or more than two matrices, the given matrices should be of the same order.
\[A\times B=[{{c}_{ij}}]\] be a matrix whose order will be \[mxp.\]
e.g. \[A{{\left[ \xrightarrow[5\,\,\,\,\,\,2\,\,\,\,\,\,1]{2\,\,\,\,\,\,1\,\,\,\,\,\,3} \right]}_{\,2\,\times \,3}}\] &
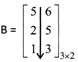
![]()
![]()
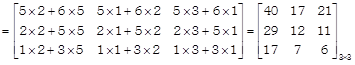
Hence \[A\times B\ne B\times A.\]
(a) Row Matrix: A matrix having order \[1\times n\] i.e. which has only one row, is said to be row matrix.
e.g. \[A={{[1\,\,2\,\,3\,\,4\,\,5]}_{\,1\,\times \,5}}\]
(b) Column Matrix: A matrix, having order \[m\times 1\] i.e. which has only one column is said to be column matrix.
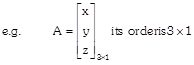
(c) Square Matrix: A matrix having same no. of rows & columns is said to be square matrix.
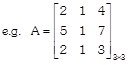
(d) Diagonal Matrix: A square matrix is said to be diagonal matrix if all of its non-diagonalelements are zero.
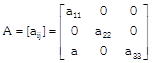
i.e \[{{a}_{ij}}=0\,\,if\,\,i\ne \,j\,=\,\,something\,\,if\,i=j\]
![]()
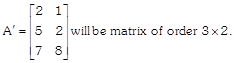
(i) If A and B be the two matrix of the same order then \[{{(A\,\pm B)}^{c}}={{A}^{c}}\pm {{B}^{c}}\,\,\,\,\,\,\,\,\,\,\,m\times n\]
(ii) If A be the matrix and k be any scalar quantity then \[{{(kA)}^{c}}=k.{{A}^{c}}\]
(iii) If A & B be two matrix of order \[m\times n\] and \[n\times p\] respectively, there exists the multiplication between A & B. Then
\[{{(A\times B)}^{c}}={{B}^{c}}.\,{{A}^{c}}\]
(iv) The double transpose of any matrix gives its primal matrix i.e. \[{{({{A}^{c}})}^{c}}=A.\]
i.e. \[A=A'\]
The matrix,\[A={{[{{a}_{ij}}]}_{\,m\,\times \,n}}\] is said to symmetric matrix if \[{{a}_{ij}}={{a}_{ji}}.\]
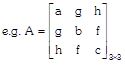
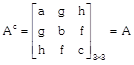
i.e. \[A=-A'\]
The matrix, \[A={{[{{a}_{ij}}]}_{\,m\,\times \,m}}\] is said to symmetric matrix if
e.g. \[{{a}_{ij}}=-{{a}_{ji}}\,\,\,\forall \,\,i\And j\]
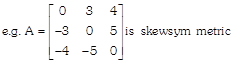
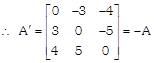
Note: Every square matrix is written as the sum of the symmetric & skew symmetric matrices.
i.e. If A is a square matrix then \[A=\frac{1}{2}[(A+{{A}^{c}})+(A-{{A}^{c}})]\]
Where \[A+{{A}^{c}}=\] symmetric matrix & \[A-{{A}^{c}}=\] skew symmetric matrix.
(i) If A &B be two symmetric (or skew symmetric) matrices, then A + B will be symmetric matrix (or skew symmetric matrix).
(ii) If A is symmetric (or skew symmetric) matrix and k is any scalar quantity, then (kA) is a symmetric (or skew symmetric) matrix.
(iii) If A and B are symmetric matrices of the same order, the product AB is symmetric iff AB = BA
(iv) The matrix B' AB is symmetric or skew symmetric accordingly as A is symmetric or skew symmetric.
(v) If A and B are symmetric matrices of the same order, then
(a) \[AB-BA\]is a skew symmetric matrix.
(b) \[AB+BA\]is a symmetric matrix.
(vi) All positive integral powers of a symmetric (or skew symmetric) matrix will be symmetric (or skew-symmetric) matrix.
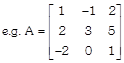
In \[{{R}_{1}}\]row,
co-factor of 1 i.e. \[{{a}_{11}}=3\]
co-factor of \[-1\]i.e. \[{{a}_{12}}=-12\]
co-factor of 2 i.e. \[{{a}_{13}}=6\]
In \[{{R}_{2}}\]row,
co-factor of 2 i.e. \[{{a}_{21}}=-(-1)=1\]
co-factor of 3 i.e. \[{{a}_{22}}=5\]
co-factor of 5 i.e. \[{{a}_{23}}=-(-2)=2\]
In \[{{R}_{3}}\]row,
co-factor of \[-2\]i.e. \[{{a}_{31}}=-11\]
co-factor of 0 i.e. \[{{a}_{32}}=-(5-4)=-1\]
co-factor of 1 i.e. \[{{a}_{33}}=3+2=5\]
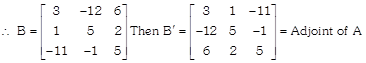
Properties of adjoint of a matrix:
(i) If A is the square matrix of order m, then adjoint A' = (adj of A)
(ii) If A & B be two the square matrices of the same order, then adj(AB) = (adj A).(adj B)
(iii) The adjoint of a diagonal matrix is a diagonal matrix.
(iv) adj(adj A) \[=\,\,|A|{{\,}^{n\,-\,2}}.\] A where A is the non-singular matrix
AB = BA = I
Where I is the unit matrix.
i.e. It is represent by \[{{A}^{-1}}\]
So, \[{{A}^{-1}}=\frac{\alpha dj\,\,of\,\,A}{|A|}\]
i.e. A.\[{{A}^{-1}}={{A}^{-1}}.\] \[A=I\]
(i) The inverse of the square of a matrix exists iff A is non-singular.
(ii) Double inverse of the square matrix is primal matrix A itself, i.e. \[{{({{A}^{-1}})}^{-1}}=A\]
(iii) If A & B be two invertible matrices of the same order m x m then AB is also invertible & moreover\[{{(AB)}^{-1}}={{B}^{-1}}{{A}^{-1}}\]
(iv) The inverse of the transpose of a matrix A is equal to the transpose of the inverse of matrix A.
i.e. \[{{(A')}^{-1}}=({{A}^{-1}})'\]
(v) If A is the symmetric matrix such that\[|A|\,\,\ne 0\], then \[{{A}^{-1}}\] is also the symmetric matrix.
Solved Examples
Sol. \[\therefore \,\,\,BA=B\]
Right multiply B on both such
\[\therefore \,\,(B\,A)B=B.\,\,\,B\] \[B.(A\,B)={{B}^{2}}\]
\[\Rightarrow B.\,\,A={{B}^{2}}\,\,\,\,\,\,\,\,\,[\because A\,\,B=A]\]
\[\Rightarrow B={{B}^{2}}\]
\[\Rightarrow {{B}^{2}}=B\]
Sol. ![]()
![]()
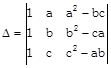
Sol.
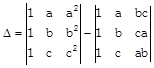
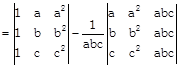
In 2nd put \[{{R}_{1}}\to a.{{R}_{1}}\] \[{{R}_{2}}\to b{{R}_{2,}}{{R}_{3}}\to c{{R}_{3}}\]
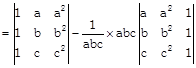
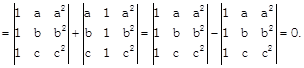
You need to login to perform this action.
You will be redirected in
3 sec
