12th Class Mathematics Three Dimensional Geometry Notes - Mathematics Olympiads - Three D Geometry

                                                                               Three Dimensional Geometry

·                

• Direction cosines: Let P(a, b, c) be any point. We join P to origin O. Let the line OP makes an angle \[\alpha ,\beta ,\gamma \] with positive direction of x-axis, y-axis and z-axis respectively. Then \[\cos \alpha ,\cos \beta \] and \[\cos \gamma \] are called the direction cosine of the directed line OP. If the angle is measured in clockwise direction then the direction angles are replaced by their supplements i.e. \[\pi -\alpha ,\]\[\pi -\beta ,\]and\[\pi -\gamma \] respectively. It is generally denoted by \[\ell \], m and n respectively i.e. \[\ell =\cos \alpha ,\]\[m=\cos \beta \]and \[n-\cos \gamma \]

\[\Rightarrow \] \[{{\ell }^{2}}+{{m}^{2}}+{{n}^{2}}=1\]

 

• Direction Ratio: The three number a, b, c proportional to the direction cosines \[\ell \]m, n of a vector are known as the direction ratio of the vector.

 

 

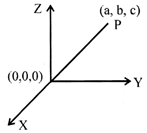
Consider P(a, b, c) be any point in the space at length r from the origin to the axis. Here a, b and c are said to be direction ratios.

\[\therefore OP=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\] (By distance formula)

\[|r|=\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}\]

Note: Direction cosine is proportional to the direction ratio.

Let a, b, c be d.r.,s of the line OP and its d.c.'s be \[\ell \],m and n respectively.

Then \[\frac{\ell }{a}=\frac{m}{b}=\frac{n}{c}=K\] (say)

Convesion from direction ratios (d.r.'s) to direction cosines (d.c.'s)

\[\ell =\pm \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

\[m=\pm \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\] and \[n=\pm \frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

 

• Some salient features of d.r.'s and d.c.'s

If \[\vec{r}=a\hat{i}+b\hat{j}+c\hat{k}\]

Then a, b and c be the d.r.'s of r and d.c.'s of r is given by

\[\ell =\frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\],\[m=\frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]and \[n=\frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]

 

• The D.R. of the line joining two points \[P({{x}_{1}},{{y}_{1}},{{z}_{1}})\]and\[Q({{x}_{2}},{{y}_{2}},{{z}_{2}})\]are \[{{x}_{2}}-{{x}_{1}},{{y}_{2}}-{{y}_{1}}\]and \[{{z}_{2}}-{{z}_{1}}\]and its direction cosines (d.c.'s) be \[\frac{{{x}_{2}}-{{x}_{1}}}{|PQ|},\]\[\frac{{{y}_{2}}-{{y}_{1}}}{|PQ|}\] and \[\frac{{{z}_{2}}-{{z}_{1}}}{|PQ|}\]respectively.
• Direction cosines of x-axis, y-axis and z-axis be written as (1, 0, 0) (0, 1, 0) and (0, 0, 1) respectively.

 

• Angle between two vectors: If \[\theta \] be the angle between two vectors whose direction cosines are

\[{{\ell }_{1}},{{m}_{1}},{{n}_{1}}\]and \[{{\ell }_{2}},{{m}_{2}},{{n}_{2}}\]then

\[\cos \theta ={{\ell }_{1}}{{\ell }_{2}}+{{m}_{1}}{{m}_{2}}+{{n}_{1}}{{n}_{2}}\]

and\[\sin \theta =\sqrt{{{({{m}_{2}}{{\ell }_{1}}-{{m}_{1}}{{\ell }_{2}})}^{2}}-{{({{m}_{1}}{{n}_{2}}-{{m}_{2}}{{n}_{1}})}^{2}}+{{({{\ell }_{2}}{{n}_{1}}-{{\ell }_{1}}{{n}_{2}})}^{2}}}\]

 

• If\[{{\ell }_{1}}{{\ell }_{2}}+{{m}_{1}}{{m}_{2}}+{{n}_{1}}{{n}_{2}}=0\], then both vectors will be orthogonal.

 

• If\[\frac{{{\ell }_{1}}}{{{\ell }_{2}}}=\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{n}_{1}}}{{{n}_{2}}}\], then both vectors are parallel.

 

• Angle in the terms of direction ratios (d.r.'s).

 

If \[\vec{a}={{a}_{1}}\vec{i}+{{b}_{1}}\vec{j}+{{c}_{1}}\vec{k}\]

and\[\vec{b}+{{a}_{2}}\vec{i}+{{b}_{2}}\vec{j}+{{c}_{2}}\vec{k}\]be the two vectors, then their direction ratios be \[{{a}_{1}},{{b}_{1}},{{c}_{1}}\] and \[{{a}_{2}},{{b}_{2}},{{c}_{2}}\] respectively. Let \[\theta \] is the .angle between these two vectors. Then \[\cos \theta =\]\[\frac{{{a}_{1}}{{a}_{2}}+{{b}_{1}}{{b}_{2}}+{{c}_{1}}{{c}_{2}}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}.\sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}.\]

 

• If two vectors are orthogonal, then \[{{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}}+{{c}_{1}}.{{c}_{2}}=0\]

 

• If two vectors are parallel, then \[\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\]

 

• Projection of the joining of the two points on a line: If \[P({{x}_{1}},{{y}_{1}},{{z}_{1}})\] and \[Q({{x}_{2}},{{y}_{2}},{{z}_{2}})\] are two points the length of the projection of PQ on a line whose direction cosine are \[\ell \], m and n is \[=({{x}_{2}}-{{x}_{1}}).\ell +({{y}_{2}}-{{y}_{1}}).m+({{z}_{2}}-{{z}_{1}}).n\]

 

Solved Examples

1. Find the projection of the line segment joining the points (1, 1, 2) and (3, 4, 1) on the line whose direction ratios are (2, 3, 6).

Sol.      Here \[P\equiv (1,1,2)\]

\[Q\equiv (3,4,1)\]

Given \[d.r.'s\equiv (2,3,6)\]

The first step is to find the \[d.c.'s\]

\[\ell =\frac{2}{\sqrt{{{2}^{2}}+{{3}^{2}}+{{6}^{2}}}}=\frac{2}{7}\],\[m=\frac{3}{7}\]and\[n=\frac{6}{7}.\]

\[\therefore \]Projection of the line joining the points (1, 1, 2) and (3, 4, 1) on the line whose \[d.c.'s\]are\[\left( \frac{2}{7},\frac{3}{7},\frac{6}{7} \right)\], is

\[=(3-1)\times \frac{2}{7}+(4-1)\times \frac{3}{7}+(1-2)\times \frac{6}{7}\]\[=2\times \frac{2}{7}+3\times \frac{3}{7}+\frac{-6}{7}\]\[=\frac{4+9-6}{7}=\frac{7}{7}=1\]

 

• Plane: A plane is a two dimensional surface. The general equation of the plane is written as \[ax+by+cz+=0,\] where a, b, c are not all zero.

Note:

(i)  Equation of xy plane is \[z=0\]

(ii) Equation of yz plane is \[x=0\]

(iii) Equation of zx plane is \[y=0\]

(iv) Equation of the any plane parallel to xy plane is \[z=c\]

(v) Equation of the any plane parallel to yz plane \[x=a\] &

(vi) Equation of any plane parallel to zx plane is \[y=b\] etc.

 

• Equation of a plane in normal form

(i) Vector form: If \[\vec{n}\] be a unit vector normal to a given plane & p be the length of perpendicular from the origin to the plane, then the equation of the plane is written as \[\vec{r}.\vec{n}=p\]

(ii) Cartesian form: If\[\ell \], m, n be the direction cosines of the normal to given plane and P is distance from the origin to the plane, then the equation of the plane is \[\ell x+my+nz=p\]

 

• Length of perpendicular from a point on the line: The length of the perpendicular from a point \[A({{r}_{1}})\]upon the line \[r=a+\lambda \,b\]is given by

\[=\frac{|(a-{{r}_{1}})\times b|}{|b|}\]

 

• Skew lines: Two straight lines which are not parallel and which do not intersect, are known as skew lines. Obviously, two such lines can never be coplanar.

 

• Shortest Distance between two skew lines: Let AB and PQ are the two skew lines. Let a line SD is perpendicular to AB and PQ. Thus, the length of the SD is the shortest distance between two lines AB and PQ.

 

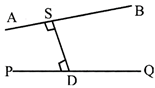
Let the two lines AB and PQ are respectively, \[{{r}_{1}}={{a}_{1}}+\lambda {{b}_{1}}\]and \[{{r}_{2}}={{a}_{2}}+\mu {{b}_{2}}.\]

Then the shortest distance between the lines \[{{r}_{1}}={{a}_{1}}+\lambda {{b}_{1}}\]and \[{{r}_{2}}={{a}_{2}}+\mu {{b}_{2}}.\]is given by

\[d=\frac{|({{a}_{2}}-{{a}_{1}}).({{b}_{1}}\times {{b}_{2}})}{|{{b}_{1}}\times {{b}_{2}}|}\]

Note: The shortest distance between two parallel lines\[r={{a}_{1}}+lb\]&\[r={{a}_{2}}+\mu b\]are\[d=\frac{({{a}_{2}}-{{a}_{1}})\times b|}{|b|}\]

• Cartesian Form of the equation of two lines and angle between them

\[\frac{x-{{x}_{1}}}{{{a}_{1}}}=\frac{y-{{y}_{1}}}{{{b}_{1}}}=\frac{z-{{z}_{1}}}{{{c}_{1}}}\] & \[\frac{x-{{x}_{2}}}{{{a}_{2}}}=\frac{y-{{y}_{2}}}{{{b}_{2}}}=\frac{z-{{z}_{2}}}{{{c}_{2}}}\]

Let \[\theta \] be the angle between them, then \[\cos \theta =\frac{{{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}}+{{c}_{1}}.{{c}_{2}}}{\sqrt{a_{1}^{2}+b_{1}^{2}+c_{1}^{2}}\times \sqrt{a_{2}^{2}+b_{2}^{2}+c_{2}^{2}}}\]

 

• Perpendicular From a point to a line: Let the equation of the line be

\[\frac{x-a}{\ell }=\frac{y-b}{m}=\frac{z-c}{n}=r\]be the given point. Then

 

 

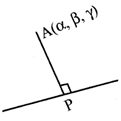
\[\therefore \]   \[P\equiv (\ell r+a,mr+b,nr+c)\]

\[\therefore \]   Length of the perpendicular is AP

\[=\sqrt{{{(\ell r+a-\alpha )}^{2}}+{{(mr+b-\beta )}^{2}}+{{(nr+c-\gamma )}^{2}}}\](By distance formula)

So, equation of the line AP be

where \[r=(\alpha -a)\ell +(\beta -b)m+(\gamma -c)n\]

 

• Vector equation of a line through a given point and parallel to a given vector

The vector equation of the straight line passing through given point with the position vector \[\vec{a}\] & parallel to a given vector \[\vec{b}\]is given as follows:

\[\vec{r}=\vec{a}+\lambda \,\vec{b}\]

where \[\lambda =\] scalar quantity.

Note: If \[\vec{r}\] is the position vector of the any point P(x, y, z) on the line, then \[\vec{r}=x\vec{i}+y\vec{j}+z\vec{k}\]

 

• Cartesian form: The equation of the straight line with the d.r.'s a, b, c and passing through a fixed point \[({{x}_{1}},{{y}_{1}},{{z}_{1}})\] is given as follows:

\[\frac{x-{{x}_{1}}}{a}=\frac{y-{{y}_{1}}}{b}=\frac{z-{{z}_{1}}}{c}\]

If \[\ell ,\] m & n be the direction cosines of the line, then the equation of the straight line is

\[\frac{x-{{x}_{1}}}{\ell }=\frac{y-{{y}_{1}}}{m}=\frac{z-{{z}_{1}}}{n}\]

 

Solved Examples

1. Find the equation of the line in vector and cartesian form that passes through the point with the position vector \[2\vec{i}-\vec{j}+4\vec{k}\]& is in the direction \[\hat{i}-2\hat{j}-\hat{k}.\]

Sol.      \[\overrightarrow{OA}=2\hat{i}-\hat{j}+4\hat{k}\]

\[\vec{b}=\hat{i}-2j-\hat{k}\]

\[\therefore \] Equation of the straight line be

\[\vec{r}=(2\vec{i}-\vec{j}+4\vec{k})+\lambda (\vec{i}+2\vec{j}-\vec{k})\]

\[\vec{r}=(2+\lambda )\vec{i}-(1-2\lambda )\vec{j}+(4-\lambda )\vec{k}\] (1)

Equation (1) is the eqaution of straight line in vector form. Now to find the equation of line in certesian form

Let \[\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\]                     (2)

Comparing (1) & (2), we have

\[x=2+\lambda \]           \[\Rightarrow x-2=\lambda \]

\[y=-(1-2\lambda )\]        \[\Rightarrow \left( \frac{y+1}{2} \right)=\lambda \]

\[z=4-\lambda \] \[\Rightarrow (z-4)=-\lambda \]

\[\therefore \] Equation of straight line will be

\[\frac{x-2}{1}=\frac{(y+1)}{2}=\frac{(z-4)}{-1}\]

 

• Equation of the line passing through two given points: The vector equation of a line passing through two given points with position vector \[\vec{a}\] & \[\vec{b}\] be

\[\vec{r}=\vec{a}+\lambda (\vec{b}-\vec{a})\]

 

• Cartesian form: The equation of the line passing through the two given points \[({{x}_{1}},{{y}_{1}},{{z}_{1}})\]and \[({{x}_{2}},{{y}_{2}},{{z}_{2}})\]is given by

\[\frac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\frac{z-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}}\]

 

• Angle between two straight lines:

Vector form: The angle between two lines

\[{{r}_{1}}={{a}_{1}}+\lambda \,{{b}_{1}}\] & \[{{r}_{2}}={{a}_{2}}+\mu {{b}_{2}}\]is written as

\[\cos \theta =\frac{{{b}_{1}}.{{b}_{2}}}{|{{b}_{1}}|.|{{b}_{2}}|}\]

 

Solved Example

1. Find the co-ordinates of the point where the line through the points A(3, 4, 1) and B(5, 1, 6) crosses the XY-plane.

Sol.      Equation of the straight line passes through A & B be

\[\frac{x-{{x}_{1}}}{{{x}_{2}}-{{x}_{1}}}=\frac{y-{{y}_{1}}}{{{y}_{2}}-{{y}_{1}}}=\frac{z-{{z}_{1}}}{{{z}_{2}}-{{z}_{1}}}\]

\[\Rightarrow \frac{x-3}{5-3}=\frac{y-4}{1-4}=\frac{z-1}{6-1}\]    \[\Rightarrow \frac{x-3}{2}=\frac{y-4}{-3}=\frac{z-1}{5}\]

            Let point \[P\equiv (a,b,0)\]

According to question, straight line crosses the XY-plane at P. It means the co-ordinate of point satisfies the given straight line

\[\therefore \,\,\,\frac{a-3}{2}=\frac{b-4}{-3}=\frac{0-1}{5}\]

\[\Rightarrow \frac{a-3}{2}=\frac{b-4}{-3}=\frac{0-1}{5}\]                      ……..(i)

On solving equ (i), we get

\[\frac{a-3}{2}=\frac{-1}{5}\Rightarrow 5a-15=-2\]          \[\Rightarrow 5a=13\Rightarrow a\frac{13}{5}\]

Similarly, \[\frac{b-4}{-3}=\frac{-1}{5}\]             \[\Rightarrow 5b-20=3\Rightarrow b=\frac{23}{5}\]

Hence the required point, \[P\equiv (a,b,0)\equiv \left( \frac{13}{5},\frac{23}{5},0 \right)\]

 

2. Find the vector equation of a plane which is at distance 7 units from the origin and normal to the vector \[3\vec{i}+5\vec{j}-6\vec{k}.\]

Sol.      The vector equation of a plane be

\[\vec{r}.\vec{n}=p\]

\[\because \vec{n}=\frac{{\vec{a}}}{|\vec{a}|}=\frac{3\vec{i}+5\vec{j}-6\vec{k}}{\sqrt{{{3}^{2}}+{{(5)}^{2}}+{{(-6)}^{2}}}}=\frac{3\vec{i}+5\vec{j}-6\vec{k}}{\sqrt{70}}\]

\[\Rightarrow \vec{r}.\frac{(3\vec{i}+5\vec{j}-6\vec{k}}{\sqrt{70}}=7\]

\[\Rightarrow (x\vec{i}+y\vec{j}+z\vec{k}).\frac{(3\vec{i}+5\vec{j}-6\vec{k})}{\sqrt{70}}=7\]

\[\Rightarrow 3x+5y-6z=7\sqrt{70}\]

This is the required equation of the plane.

 

3. Find the coordinates of the point where the line through (5, 1, 6) and (3, 4, 1) crosses the plane

\[2x+y+z=7\]

Sol.      Vector equation of the straight line through the points (5, 1, 6) and (3, 4, 1) be

\[\Rightarrow \vec{r}=\vec{a}+\lambda (\vec{b}-\vec{a})\]

\[\Rightarrow \vec{r}=5\vec{i}+\vec{j}+6\vec{k}+\lambda (-2\vec{i}+3\vec{j}-5\vec{k})\]

\[\Rightarrow \vec{r}=(5-2\lambda )\vec{i}+(1+3\lambda )\vec{j}+(6-5\lambda )\vec{k}\]   ….. (1)

Let \[P\equiv (a,b,c)\] be any point where the straight line crosses the plane \[2x+y+z=7.\]                  ……(2)

So, the point P must satisfies the equation (2)

\[\therefore 2a+b+c=7\]

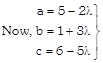
On putting the values in equation (2), we get

\[\Rightarrow 2(5-2\lambda )+1+3\lambda +6-5\lambda =7\]

\[\Rightarrow 10-4\lambda +1+3\lambda +6-5\lambda =7\]

\[\Rightarrow -6\lambda +17=7\]             \[\Rightarrow \lambda =\frac{10}{6}=\frac{5}{3}\]

Thus,

\[a=5-2\times \frac{5}{3}=\frac{5}{3}\]

\[b=1+3\times \frac{5}{3}=6\]

\[c=6-5\times \frac{5}{3}=\frac{-7}{3}\]

Hence, the required point be \[\left( \frac{5}{3},6\frac{-7}{3} \right)\].