12th Class Mathematics Vector Algebra Notes - Mathematics Olympiads -Vectior Algebra

 

                                                                                             Vector Algebra

 

·                 

• As we know that the some quantities have only magnitude and some have magnitude as well as direction, e.g. distance, force, work, current etc.

On this basis, all physical quantities are divided into two groups:

(i)  Scalar quantities.

(ii) Vector quantities.

 

• Scalar quantity: A quantity which has only magnitude and does not have direction is said to be scalar quantity. For example: distance, speed, work-done etc.

 

• Vector quantity: A quantity which has magnitude as well as direction and also obeys the addition law of triangle is said to be vector quantity. For example: Displacement, Force, Velocity etc.

 

• Representation of vectors: A vector is symbolically represented by putting an arrow sign (\[\to \]) on a letter or group of letters representing directed line segment. For example, a vector drawn from a point 0 to point A. Point 0 is called the initial point and point A is called the end point. Symbolic notation for this vector is\[\left| \left. \overrightarrow{OA} \right| \right.\] .

 

• Modulus (or magnitude) of a vector: The positive real number which is the measure of the length of the vector, is called the modulus, absolute value or length or magnitude or normal of the vector. For example, the magnitude of \[\vec{a}=2\hat{i}+3\hat{j}+5\hat{k}\]is given by, \[\left| \,\left. \vec{a}\, \right| \right.=\sqrt{{{(2)}^{2}}+{{(3)}^{2}}+{{(5)}^{2}}}\]\[=\sqrt{4+9+25}=\sqrt{38}\]

where \[\hat{i}\],\[\hat{j}\] and \[\hat{k}\]are said to be the unit vectors.

 

• Position vector: The vector which gives the position of a point, relative to a fixed point (the origin) is called position vector.

If \[P(x,y,z)\] be any point in space then position vector \[\overrightarrow{OP}=x\vec{i}+y\vec{j}+z\vec{k}\]

\[\therefore \,\,|\,\,\overrightarrow{OP}\,\,|\]\[=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\]

 

• Type of vectors:

1. Equal Vectors: Two vectors \[\vec{a}\] and \[\vec{b}\] are said to be equal, if they have the same magnitude and direction regardless of the positions of their initial points. They can be written as \[\vec{a}=\vec{b}\].

 

2. Negative of a Vector: A vector whose magnitude is the same as that of a given vector (say,\[\overrightarrow{PQ}\]), but direction is opposite to that of it, is called negative of the given vector. For example, vector \[\overrightarrow{QP}\] is negative of the vector \[\overrightarrow{PQ}\] i.e., \[\overrightarrow{QP}=-\overrightarrow{PQ}\]

 

3. Like and Unlike Vectors: Two vectors are said to be like vectors, if they have same direction. Similarly, two vectors are called unlike vectors, if they have opposite direction from each other.

 

4. Zero Vector: The vector whose initial and terminal points coincide, is called a zero vector or null vector. It is denoted as \[\vec{0}\]. Zero vector cannot be assigned a definite direction as it has zero magnitude. It is also said to have any direction. The vectors \[\overrightarrow{PP}\], \[\overrightarrow{QQ}\] represent the zero vector

 

5. Unit Vector: The vector whose magnitude is 1 unit or unity is known as unit vector. The unit vector in the direction of a given vector \[\vec{a}\] is denoted by\[\hat{a}\].

 

6. Coinitial Vectors: If two or more vectors having the same initial points, they are called coinitial vectors.

 

7. Collinear Vectors: Two or more vectors are said to be collinear if they are parallel to the same line, irrespective of their magnitudes and directions.

 

• Properties of Multiplication of a Vector by a scalar.

1. If \[m=0\], then m. \[\vec{a}=0\]
2. If m & n be two scalars, then \[m(n\vec{a})=(m.n)\vec{a}=n(m\vec{a})\]
3. If m & n be two scalars, then \[(m+n)\vec{a}=m\vec{a}+n\vec{a}\]
4. If \[\vec{a}\] and \[\vec{b}\] are two vectors and m be any \[m(\vec{a}+\vec{b})=m\vec{a}+m.\vec{b}\]

• Section Formulae:

Internal Division: Let A and B be the two points with the position vectors \[\vec{a}\] & \[\vec{b}\] respectively and let P be any point dividing AB internally in the ratio m : n. Then the position vector of P can be written

as \[\overrightarrow{OP}=\frac{m.\vec{b}+n\vec{a}}{m+n}\]

When P divides AB externally, then the position vector of P is given by,

\[\overrightarrow{OP}=\frac{m.\vec{b}-n\vec{a}}{m-n}\]

If P is the midpoint of AB, then position vector of P is given by, \[\overrightarrow{OP}=\frac{\vec{b}+\vec{a}}{2}\]

• Addition (Resultant) of two vectors:

Let \[\overrightarrow{OA}=\vec{a}\] and \[\overrightarrow{AB}=\vec{b}\] be the two vectors.

 

 

Two non-zero vectors can be added geometrically by placing the initial point of \[\overrightarrow{AB}\]at the terminal point of \[\overrightarrow{OA}\] and then finding the vector that has the same initial point as \[\overrightarrow{OA}\] and the same terminal point \[\overrightarrow{AB}\],as shown in the figure.

\[\therefore \overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{AB}\]

 

It is known as triangle law of addition.

 

• Properties of vectors additions:

1. Vector addition is commutative:

            \[\therefore \vec{a}+\vec{b}=\vec{b}+\vec{a}\]

 

2. Vector addition is associative:

For any three vectors \[\vec{a},\vec{b}\]and \[\vec{c}\], we have \[\vec{a}+(\vec{b}+\vec{c})\]\[=(\vec{a}+\vec{b})+\vec{c}\]

 

3. Existence of additive identity:

For every vector \[\vec{a}\], we have \[\vec{0}+\vec{a}=\vec{a}+\vec{0}=\vec{a}\]

Here \[\vec{0}\] is said to be null or zero vector.

 

4. Existence of additive inverse:

For a given vector \[\vec{a}\], there exists a negative vector \[-\vec{a}\], such that

\[\vec{a}+(-\vec{a})=0\]

The vector \[-\vec{a}\] is said to be the additive inverse of\[\vec{a}\].

 

• Component of a vector: If we consider a vector \[\overrightarrow{OP}\] in a three dimensional co-ordinate system, then it can be broken or resolved into x, y and z components along x, y and z axes as shown below:

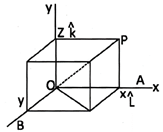
Here \[\overrightarrow{AO}\] is the component of \[\overrightarrow{OP}\] along x -axis.

 

• Linear combination of vectors:

Definition: A vector \[\vec{\ell }\]is said to be the linear combination of vectors \[\overrightarrow{a},\vec{b},\vec{c}\]...etc., if there exists scalar quantities x, y, z, ... etc. such that \[\vec{r}=x\vec{a}+y\vec{b}+z\vec{c}+\]…

 

• Collinearity of points: The necessary and sufficient condition that the three points with the position vectors \[\vec{a},\vec{b},\vec{c}\]be collinear is that there exist three scalar \[\ell \], m, and n, where \[\ell \ne 0,\]\[m\ne 0\]and \[n\ne 0\] such that \[\ell \vec{a}+m\vec{b}+n\vec{c}=0\] provided that\[\ell +m+n=0\]

 

• Solved Examples

1. Prove that the points \[\vec{a}-2\vec{b}+3\vec{c},\]\[2\vec{a}+3\vec{b}-4\vec{c}\]and \[7\vec{b}+10\vec{c}\] are collinear.

Sol. 1^st Method: Let the given points be A, B and C related to any origin O. Now if we can find the three scalars\[\ell \], m and n such that\[\ell .\overrightarrow{OA}+m.\overrightarrow{OB}+n.\overrightarrow{OC}=0\], provided that \[\ell +m+n=0\]then A, B, C will be collinear

Now, \[\ell .\overrightarrow{OA}+m.\overrightarrow{OB}+n.\overrightarrow{OC}=0\]

\[=\ell \,(\vec{a}-2\vec{b}+3\vec{c})+m(2\vec{a}+3\vec{b}-4\vec{c})\]

\[+n(-7\vec{b}+10\vec{c})=0\]

\[=(\ell +2m)\vec{a}+(-2\ell +3m-7n)\vec{b}\]

\[+(3\ell -4m+10n)\vec{c}=0\]

Equating the coefficient, we get

\[\ell +2m=0\]               ........ (i)

\[-2\ell +3m-7n=0\]                       ........ (ii)

and       \[3\ell -4m+10n=0\]             ........ (iii)

On solving equations, (i), (ii) and (iii), we get

\[\ell =2,\]\[m=-1\]and\[n=-1\]

\[\because \]       \[\ell +m+n=2-1-1=0\]

Hence the given points are collinear.

 

2^nd    Method:

Let the given points be A, B, C respectively, we have \[\overrightarrow{AC}=\overrightarrow{OC}-\overrightarrow{OA}\]

\[=(-7\vec{b}+10\vec{c})-(\vec{a}-2\vec{b}+3\vec{c})=\overrightarrow{-a}-5\vec{b}+7\vec{c}\]

\[\overrightarrow{BA}=\overrightarrow{OA}-\overrightarrow{OB}=(\vec{a}+2\vec{b}+3\vec{c})-(2\vec{a}+3\vec{b}-4\vec{c})=\overrightarrow{-a}-5\vec{b}+7\vec{c}\]

\[\overrightarrow{BA}\]   \[=-\vec{a}-5\vec{b}+7\vec{c}\]

Hence \[\overrightarrow{AC}=\overrightarrow{BA}\]

\[\therefore \] Points A, B and C are collinear.

 

2. Find\[|\vec{x}|\], if for a unit vector \[\vec{a},\]\[(\vec{x}-\vec{a}).(\vec{x}+\vec{a})=12.\]

            Sol.      \[\because \]\[(\vec{x}-\vec{a}).(\vec{x}+\vec{a})=12\]

                        \[\Rightarrow \vec{x}.\vec{x}-\vec{a}.\vec{x}+\vec{x}.\vec{a}-\vec{a}.\vec{a}=12\]

                        \[\Rightarrow \,\,|\vec{x}{{|}^{2}}-1=12\]

                        \[\Rightarrow \,\,|\vec{x}{{|}^{2}}=12+1=13\]

                        \[\Rightarrow \,\,|\vec{x}|=\sqrt{13}\]

 

3. Show that the points A, B and C with the position vectors, \[\vec{a}=3\hat{i}-4\hat{j}-4\hat{k},\]\[\vec{b}=2\hat{i}-\hat{j}+\hat{k}\]and\[\vec{c}=\hat{i}-3\hat{j}-5\hat{k},\] respectively form the vertices of a right angled triangle.

Sol.      \[\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=2\hat{i}-\hat{j}+\hat{k}-(3\hat{i}-4\hat{j}-4\hat{k})=-\hat{i}+3\hat{j}+5\hat{k}\]

            \[\overrightarrow{BC}=\overrightarrow{OC}-\overrightarrow{OB}=\hat{i}-3\hat{j}+5\hat{k}-(2\hat{i}-\hat{j}-\hat{k})=-\hat{i}+2\hat{j}+6\hat{k}\]

            \[\overrightarrow{CA}=\overrightarrow{OA}-\overrightarrow{OC}=3\hat{i}-4\hat{j}+4\hat{k}-(\hat{i}-3\hat{j}-5\hat{k})=2\hat{i}-\hat{j}+\hat{k}\]

            Now \[|\overrightarrow{BC}|\,\,=\,\,\sqrt{{{(-1)}^{2}}+{{(-2)}^{2}}+{{(-6)}^{2}}}={{(41)}^{2}}\]

\[|\overrightarrow{AB}|\,\,=\,\,\sqrt{{{1}^{2}}+{{3}^{2}}+{{5}^{2}}}\]\[=\sqrt{35}\]and\[|\overrightarrow{CA}|\,\,=\,\,\sqrt{{{2}^{2}}+{{1}^{2}}+{{1}^{2}}}=\sqrt{6}\]

            Thus, \[|\overrightarrow{BC}{{|}^{2}}\,=\]\[|\overrightarrow{AB}{{|}^{2}}+|\overrightarrow{CA}{{|}^{2}}=35+6=41\]

Hence, the point A, B and C are the vertices of a right angled triangle.

 

• Scalar product of two vectors: Let \[\vec{a}\] and \[\vec{b}\] be any two vectors and \[\theta \] is the angle between them. Then, the scalar product of two vectors \[\vec{a}\] and \[\vec{b}\] is denoted by \[\vec{a}\,.\,\vec{b}\] and is defined as \[\vec{a}\,.\,\vec{b}=\,\,|\vec{a}||\vec{b}|cos\theta =\]scalar quantity

 

• Some basic properties:

(i)  If the vectors \[\vec{a}\] and \[\vec{b}\] are perpendicular then:

\[\cos \theta =0\]and hence \[\vec{a}\,.\,\vec{b}=0\]

(ii) Unit vectors: Let i,] and k be unit vectors

Then \[\hat{i}\,.\,\,\hat{i}={{i}^{2}}=1\]

\[j.\hat{j}={{j}^{2}}=1\]

\[\hat{k}.\hat{k}={{k}^{2}}=1\]

Scalar product of two like unit vectors is 1 whereas the scalar product of two unlike unit vector is zero i.e.

\[\hat{i}.\hat{j}=\hat{j}.\hat{k}=\hat{k}.\hat{i}=0.\]

(iii) Scalar product is \[\vec{a}.\vec{b}=\vec{b}.\vec{a}\] commutative i.e.

(iv) \[m\vec{a}.n\vec{b}=mn(\vec{a}.\vec{b})\]

(v) \[\vec{a}.(\vec{b}+\vec{c})=\vec{a}\,.\,\vec{b}+\vec{a}\,.\,\vec{c}\] (distributive law)

(vi) Let \[\vec{a}={{a}_{1}}\hat{i}+{{b}_{1}}\hat{j}+{{c}_{1}}\hat{k}\]\[\vec{b}={{a}_{2}}\hat{i}+{{b}_{2}}\hat{j}+{{c}_{2}}\hat{k}\]

Then \[\vec{a}.\vec{b}={{a}_{1}}.{{a}_{2}}+{{b}_{1}}.{{b}_{2}}+{{c}_{1}}.{{c}_{2}}\]

(vii) Rules of sign:

\[\vec{a}.(-\vec{b})=-\vec{a}.\,\vec{b}\]

\[(-\vec{a}).\vec{b}=-\vec{a}.\,\vec{b}\]

\[(-\vec{a}).(-\vec{b})=\vec{a}.\,\vec{b}\]

(viii) Geometrical Interpretation: The scalar product (dot product) \[\vec{a}\,.\,\vec{b}\] may be defined as the product of \[|\vec{a}|\] and the projection of \[\vec{b}\] on \[\vec{a}\] or product of \[\vec{b}\]and the projection of \[\vec{a}\]on\[\vec{b}\].

 

Solved Example

1. Find the cosine of the angle between the vectors \[\vec{a}=2\hat{i}+2\hat{j}-\hat{k}\] and \[\hat{b}=6\hat{i}+3\hat{j}-2\hat{k}\]

            Sol. \[\because \]\[\vec{a}\,.\,\vec{b}=(2\hat{i}+2\hat{j}-\hat{k}).(6\hat{i}-3\hat{j}+2\hat{k})=2\times 6+2\times (-3)+(-1).2\]

            \[=12-6-2=4\]

\[\because \]We know that \[\vec{a}\,.\,\vec{b}=\,\,|\vec{a}|.|\vec{b}|\cos \theta \]

Now, \[|\vec{a}|\,\,=\sqrt{{{2}^{2}}+{{2}^{2}}+{{1}^{2}}}=\sqrt{9}=3\]

\[|\vec{b}|\,\,=\sqrt{{{6}^{2}}+{{3}^{2}}+{{2}^{2}}}=\sqrt{49}=7\]

\[\therefore \vec{a}\,.\,\vec{b}=\,\,|\vec{a}||\vec{b}|cos\theta \]

\[\cos \theta =\frac{\vec{a}\,.\,\vec{b}}{|\vec{a}||\overrightarrow{b|}}=\frac{4}{3\times 7}=\frac{4}{21}\]

 

• Vector or Cross product of two vectors: The cross or vector product of two vectors \[\vec{a}\]and\[\vec{b}\], denoted by \[\vec{a}\times \vec{b}\]and is defined as a vector v whose magnitude is equal to \[|\vec{a}|.|\vec{b}|\sin \theta \] and its direction is normal to the plane of \[\vec{a}\] and\[\vec{b}\], the direction of v being such that an anticlockwise rotation about v through an angle of not more than \[180{}^\circ \] carries \[\vec{a}\] into \[\vec{b}\].

Thus if \[\hat{n}\] be the unit vector normal to the plane of \[\vec{a}\] and \[\vec{b}\] then,

\[\vec{a}\times \vec{b}=\,\,|\vec{a}|.|\vec{b}|.\sin \theta .\hat{n}\]

Corollary: \[\vec{a}\times \vec{b}=0\]

 

• Some Basic Properties of Cross Product:

(i) The vector product does not satisfy the commutative law i.e. \[\vec{a}\times \vec{b}=-\vec{b}\times \vec{a}\]

(ii) Rules of sign:

\[(-\vec{a})\times \vec{b}=-\vec{a}\times \vec{b}\]

\[\vec{a}\times (-\vec{b})=-\vec{a}\times \vec{b}\]

\[(-\vec{a})\times (-\vec{b})=\vec{a}\times \vec{b}\]

(iii) Distributive law:

\[\vec{a}\times (\vec{b}+\vec{c})=\vec{a}\times \vec{b}+\vec{a}\times \vec{c}\]

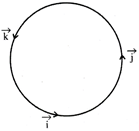
(iv) Unit vectors:

\[\vec{i}\times \vec{i}=\vec{j}\times \vec{j}=\vec{k}\times \vec{k}=0\]

\[\vec{i}\times \vec{j}=\vec{k}\]\[\Rightarrow \vec{j}\times \vec{i}=-\vec{k}\]

\[\vec{j}\times \vec{k}=\vec{i}\]\[\Rightarrow \vec{k}\times \vec{j}=-\vec{i}\]

\[\vec{k}\times \vec{i}=\vec{j}\]\[\Rightarrow \vec{i}\times \vec{k}=-\vec{j}\]

 

(v) Let \[\vec{a}={{a}_{1}}\hat{i}+{{b}_{1}}j+{{c}_{1}}\hat{k}\]

\[\vec{b}={{a}_{2}}\hat{i}+{{b}_{2}}j+{{c}_{2}}\hat{k}\]

\[+\,\,\hat{k}({{a}_{1}}.{{b}_{2}}-{{a}_{2}}.{{b}_{1}})\]

(vi) Geometrical Interpretation:

\[\vec{a}\times \vec{b}\]represents a vectors whose magnitude is equal to the area of the parallelogram of which \[\vec{a}\] and \[\vec{b}\] are adjacent sides.

Note: \[\frac{1}{2}\vec{a}\times \vec{b}\]is the vectorial area of the triangle whose adjacent sides are \[\vec{a}\]and\[\vec{b}\].

Solved Examples

1. Prove the following identify:

            \[{{(\vec{a}.\vec{b})}^{2}}+{{(\vec{a}\times \vec{b})}^{2}}={{a}^{2}}.{{b}^{2}}\]

            Sol. \[\because {{(\vec{a}.\vec{b})}^{2}}={{(|\vec{a}|.|\vec{b}|.\cos \theta )}^{2}}={{a}^{2}}.{{b}^{2}}.{{\cos }^{2}}\theta \]

\[{{(\vec{a}\times \vec{b})}^{2}}={{[|\vec{a}|.|\vec{b}|.sin\theta .\hat{n}]}^{2}}={{a}^{2}}.{{b}^{2}}.si{{n}^{2}}\theta \]

where \[\hat{n}\]is the unit vector.

L.H.S.\[={{(\vec{a}.\vec{b})}^{2}}+{{(\vec{a}\times \vec{b})}^{2}}={{a}^{2}}{{b}^{2}}.{{\cos }^{2}}\theta +{{a}^{2}}.{{b}^{2}}.{{\sin }^{2}}\theta \]

\[={{a}^{2}}{{b}^{2}}(co{{s}^{2}}\theta +{{\sin }^{2}}\theta )={{a}^{2}}{{b}^{2}}=\]R.H.S. Hence proved

 

2. Find\[|\vec{a}\times \vec{b}|\], if \[\vec{a}=\hat{i}-7\hat{j}+7\hat{k}\]and \[\vec{b}=3\hat{i}-2\hat{j}+2\hat{k}\].

            Sol.

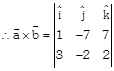
            \[=\hat{i}(-14+14)-\hat{j}(2-21)+\hat{k}(-2+21)=0\hat{i}=19\vec{j}-19\vec{k}\]

            \[\therefore \]\[|\vec{a}\times \vec{b}|\,\,=\sqrt{{{(-19)}^{2}}+{{(19)}^{2}}}=\sqrt{361+361}=\sqrt{2\times 361}=19\sqrt{2}\]