12th Class Mental Ability Time and Clock Notes - Time and Clocks

Notes - Time and Clocks

Category : 12th Class

Time and Clocks

Time and Clock

The face or dial of a watch is a circle whose circumference is divided into 60 equal parts, called minute spaces.

A clock has two hands, the smaller one is called the hour hand or short hand while the larger one is called the minute hand or long hand.

In 60 minutes, the minute hand gains 55 minutes on the hour hand.
In every hour, both the hands coincide once.
The hands are in the same straight line when they are coincident or opposite to each other.
When the two hands are at right angles, they are 15 minute spaces apart.
When the hand’s are in opposite directions, they are 30 minute spaces apart.
Angle traced by hour hand in 12 hours \[=360{}^\circ \].
Angle traced by hour hand in one hour \[=30{}^\circ \].
Angle traced by hour hand in one minute \[=\text{ }0.5{}^\circ \].
Angle traced by minute hand in 60 minutes \[=360{}^\circ \].
Too Fast and Too Slow: If a watch or a clock indicates \[8:15\], when the correct time 8 is said to be 15 minutes too fast.

On the other hand, if it indicates \[7:45\], when the correct time is 8, it is said to be 15 minutes too slow.

Example:

A clock shows the time as \[\mathbf{3}:\mathbf{30}\]pm if the minute hand gains 2 minutes every hour, how many minutes will the clock gain by 6 am?

(a) 20 minutes (b) 29 minutes

(e) None of these

Ans. (b)

Explanation: Hours between \[3:30\] pm and 6 am are \[=14\frac{1}{2}\].

So, numbers of minutes gained will be \[=14\frac{1}{2}\,\,\times \,\,2\,\,=\,\,29\] minutes.

Two watches, one of which gained at the rate of 1 minute and other lost at the rate of 1 minute daily, were set correctly at noon on the 1st January 1978. When did the watches indicate the same time?

(a) Dec 30, 1978 noon (b) Dec 25, 1978 noon

(e) None of these

Ans. (c)

Explanation: The first watch gains on the second watch \[1+1=2\] minutes in a day.

The watch will indicate the same time when the one has gained 12 hours on the other

As 2 minutes is gained in one day.

So 12 hours is gained \[=1/2\times 12\times 60=360\text{ }days\]

Counting 360 days from 1st Jan 1978, we get Dec 27, 1978.

How many times do the hands of a clock coincide between 11 O’clock and 1 O’clock?

(a) 0 (b) 1

(e) None of these

Ans. (b)

Explanation: Between 11 O’clock and 1 O’clock the hands of a clock coincide only once. So, the correct answer is (b).

A clock is set at 5 am. The clock loses 16 minutes in 24 hours. What will be the right time when the dock indicates 10 pm on the 3rd day.

(a) \[11:15\] pm (b) 11 pm

(e) None of these

Ans. (b)

Explanation: Time from 5 am of a particular day to 10 pm on the 4^th day is 89 hours. Now, the clock loses 16 minutes in 24 hrs or in other words we can say that 23 hours 44 minutes of this clock is equal to 24 hour of the correct clock.

or \[\left( 23+\frac{44}{60}=\frac{356}{15} \right)\] hours of this clock = 24 hours of the correct clock.

\[\Rightarrow \] 89 hours of this clock \[=\,\,\left( \frac{24\times 15}{356}\times 89 \right)\] hours of correct clock.

= 90 hours of the correct clock.

Therefore, it is clear that in 89 hours this clock loses 1 hour and hence the correct time is 11 pm when this clock shows 10 pm.

At what time between 4 and 5 O’clock will the hands of a watch point in opposite directions?

(a) 45 minutes past 4 (b) 40 minutes past 4

Ans. (d)

Explanation: At 4 O’clock both the hands are 20 minutes spaces apart and for having in the opposite direction they have to be 30 minute spaces apart.

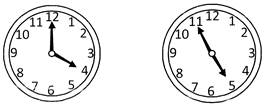
From figure (i) and figure (ii) it is clear, that minute hand has to travel \[\left( 20+30 \right)\] minute spaces in order to be in opposite direction to each other. Now 55 minute spaces is gained in 60 minutes.

Therefore, 50 minute spaces will be gained in \[\left( \frac{60}{55}\times 60 \right)\] minutes or \[54\frac{6}{11}\] minutes.

Hence, the hands of the clock will be in opposite direction at \[54\frac{6}{11}\] minutes past 4.

Therefore, (d) is the correct answer.

Find the exact time between 7 am and 8 am when the two hands of a watch meet.

(a) 7 hrs 30.18 minute (b) 7 hrs 35.18 minute

(e) None of these

Ans. (c)

Explanation: At 7 am, the minute hand is 35 minute spaces behind the hour hand 55 minute spaces are gained in 60 minute

So 35 minute spaces will be gained in 38.18 minute.

Calendar

Days in a Week

There are seven days in a week - Sunday, Monday, Tuesday, Wednesday, Thursday, Friday and Saturday.

If today is Monday then,

Tomorrow (coming day) will be - Tuesday
Day after tomorrow will be - Wednesday
Yesterday (previous day) was - Sunday
Day before yesterday was - Saturday
Day after 7 days (or a week) - Monday
Day before 7 days (or a week) - Monday
Day before or after 7 days or a multiple of 7 is same as present day.

Example

If the day before yesterday was Thursday, when will Sunday be?

(a) Tomorrow (b) Today

(e) None of these

Ans. (a)

Explanation: If day before yesterday was Thursday, then today is Saturday - Therefore tomorrow will be Sunday.

Suganya went to see a movie nine days ago. She goes to the moves only on Thursday. What day of the week is today?

(a) Tuesday (b) Thursday

(e) None of these

Ans. (d)

Explanation: Clearly, nine days ago, it was Thursday. Therefore today is Saturday.

Today is Wednesday, What will be the day after 98 days?

(a) Sunday (b) Monday

(e) None of these

Ans. (c)

Explanation: Every day of the week is repeated after 7 days. Hence it will be Wednesday, after 98 days.

If 1^st October is Sunday, then 1^st November will be:

(a) Sunday (b) Monday

(e) None of these

Ans. (c)

Clearly, 1st, 8th, 15th, 22nd and 29th of October are Sundays. So, 31st October is Tuesday. Therefore, 1^st November will be Wednesday.

12th Class Mental Ability Time and Clock Notes - Time and Clocks

Other Topics

Notes - Time and Clocks