2nd Class Mathematics Fractions Fraction

LEARINING OBJECTIVES

This lesson will help you to:

• define fractions, numerator and denominator
• identify fractions using objects and shapes
• differentiate between equal and unequal parts

Historical Preview

• The word fraction actually comes from the Latin “fraction” which means to break.
• It was the Arabs who added the line (drawn horizontally) which we now use to separate numerator and denominator.
• Egyptians were one of the first groups to study fractions.

Real Life Examples

• A year is divided in fraction of month is further divide into fraction of weeks. Half year is equal to 6-months.
• In schools, the time is divided into equal fractions of periods for each subject.

QUICK CONCEPT REVIEW

Halves and Quarters

Half

Rahul and Akshay were hungry. They bought a muffin cake. They shared muffin cake by dividing it into two equal parts.

When a whole object is divided into equal parts, then each part is called a fraction.

In the above example. Part 1 and Part 2 are two fractions of muffin cake.

Part 1 is one half and Part 2 is another half.

Misconcept/Concept

• Misconcept: A fraction such as \[\frac{3}{4}\]is a ‘quarter of three’
• Concept: A fraction \[\frac{3}{4}\]means ‘three parts of quarter’?

Numerator and Denominator

A fraction is made up of two numbers which are divided by a line. The number that is written below the line is known as denominator.

Denominator shows how many equal parts something has been divided into.

The number that is written above the line is known as numerator.

Numerator shows how many parts of the whole is taken.

Quarters\[\left( \frac{1}{4} \right)\]and Three-Quarters\[\left( \frac{3}{4} \right)\] .

Let us take an example.

Sam, Jatin, Ravi and Jack bought a chocolate. They cut it into 4 equal parts.

Each part is called one - quarter \[\left( \frac{1}{4} \right)\] .

Suppose, Ravi ate his part of chocolate or we can say he ate \[\left( \frac{1}{4} \right)\] of the choclate.

How much share of chocolate was now left?

3 shares are left. We can say that. \[\frac{3}{4}\]or three-quarters of chocolate was left uneaten and one-quarter of chocolate was eaten by Ravi.

Let us take another example

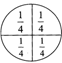
A circle can be divided into two halves, and four quarter\[\left( \frac{1}{4} \right)\]parts as shown on the left side.

EQUAL AND UNEQUAL PARTS

Suppose circle is divided into 3 equal parts. Then, each part of the circle is its one-third part.

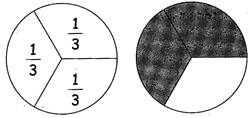
If we take any two shaded parts of these three parts together, we will have two-third of the total part.

It is written as \[\frac{2}{3}\]

The examples we have discussed so far are based on division into equal parts or fractions.

Now let us discuss about division into unequal parts.

Look at the given figure of the triangle.

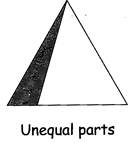
The shaded region of the triangle shows unequal part of the triangle. Here the triangle is divided into two parts but both the parts are not equal.

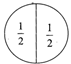
Some more examples of fraction

1. What is the fraction of each part in the following figure?

There are four equal parts, so

fraction of each part is \[\frac{1}{4}\].

1. How many parts of the whole are shaded in the above example?

Fraction is \[\frac{1}{4}\]. for each part. Two parts of whole are shaded. So, the total fraction is \[\frac{2}{4}\].

Whole is divided into four parts

1. Find out the fraction of shaded region in the adjacent figure.

The whole part is divided into 3 equal parts. So, the fraction of each part is \[\frac{1}{3}\]. The shaded

region has two equal parts. Therefore, fraction of shaded region is \[\frac{2}{3}\].

1. What fraction of total pencils are present in the box?

There are 6 pencils.

Two pencils out of 6 are taken in the box. So, the fraction of pencils in the box is \[\frac{2}{6}\].