Geometrical Shapes
Category : 3rd Class
Geometrical Shapes
Introduction
Lines, angles and rays are the basic concept of geometrical figures. Basic geometrical figure was first introduced in text by great mathematician Euclid.
Lines and Its Characteristics
Point
A precise location or place on a plane. Point is usually represented by dot.
![]()
A is a point
Line
Line is a geometrical figure formed by points moving along a fixed direction and the reverse direction. Line may be straight or curved.
![]()
Straight line Curved line
Line Segment
A straight line which links two points without extending beyond them.
![]()
AB is a line segment
Ray
A ray extends infinity in one direction, but ends at a single point in the other direction.
![]()
OA is a ray
Intersecting Point
The point where two lines meet or cross.
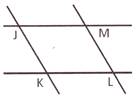
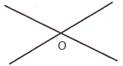
In the pictures above points J, K, L, M and O are intersecting points.
To Draw a Line Segment of a given Length
The following are the steps used to draw the line segment.
For example: Line segment of 6 cm.
Step 1: Place the ruler on the plane paper.
Step 2: Mark a point A on the paper against 0 mark of ruler.
Step 3: Mark another point B on the same paper at the length of 6 cm.
Step 4: Draw a line between A and B.

AB is the required length of 6 cm.
Ø Example
AO = 4 cm and OB = 5 cm. Find the length of AB.
A. .O .B
(a) 9 cm (b) 5 cm
(c) 8 cm (d) 7 cm
(e) None of these
Ans. (a)
Explanation: Length of AB = (4 + 5) cm = 9 cm.
Ø Example
Identify the line from the figures given below:
(a) ![]() (b)
(b) ![]()
(c) ![]() (d) All the above
(d) All the above
(e) None of these
Ans. (c)
Explanation: A line is extended from both the ends.
Angles
When two or more lines meet at a point then angle is formed. A complementary of an angle is obtained by subtracting the angle from a right angle. A supplementary angle is obtained by subtracting the angle from a straight angle.
A Right Angle
An angle whose measure is exactly 90° is a right angle.
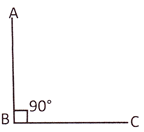
\[\angle \] ABC is a right angle
An Acute Angle
An angle whose measure is less than \[90{}^\circ \] is an acute angle.
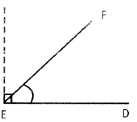
\[\angle \] DEF is an acute angle
An Obtuse Angle
An angle whose measure is greater than \[90{}^\circ \] but less than \[180{}^\circ \] is a obtuse angle.
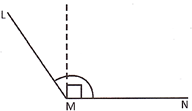
\[\angle \]LMN is an obtuse angle
Straight Angle
An angle whose measure is \[180{}^\circ \]a straight angle.
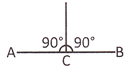
\[\angle \] ACB is straight angle
A Reflex Angle
An angle whose measure is greater than \[180{}^\circ \] but less than \[360{}^\circ \] is a reflex angle
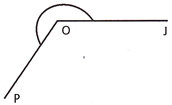
\[\angle \] JOP is a reflex angle
Triangles
A region bounded by three line segments is called triangular region and figures is called a triangle.
Equilateral Triangle
A triangle whose all sides are equal is called equilateral triangle.
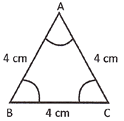
Triangle ABC is an equilateral triangle.
Isosceles Triangle
A triangle whose two sides are equal is called isosceles triangle.
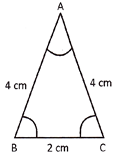
In triangle ABC AB = AC = 4 cm hence, triangle ABC is an isosceles triangle.
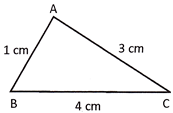
Scalene Triangle
A triangle whose sides are unequal is called scalene triangle. In the figure below side lengths of triangle ABC are not equal hence, triangle ABC is a scalene triangle.
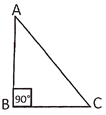
A Right Angle Triangle
A triangle whose one angle is a right angle is called right angled triangle. In the picture below triangle ABC is a right angle.
One side of a triangle is perpendicular to another side. What is the name of the triangle?
(a) Straight angle (b) Reflex angle
(c) Right angle (d) All the above
(e) None of these
Ans. (c)
Explanation: Because triangle has one right angle.
All three angles of a triangle are equal then the measurement of every angle will be?
(a) \[60{}^\circ \] (b) \[90{}^\circ \]
(c) \[30{}^\circ \] (d) \[20{}^\circ \]
(e) None of these
Ans. (a)
Explanation: Sum of all angles of triangle is\[180{}^\circ \]. So, each angle\[=\,\,\frac{180}{3}\,\,=\,\,60{}^\circ \].
You need to login to perform this action.
You will be redirected in
3 sec
