Algebra
Category : 3rd Class
Algebra
Learning Objectives
Fractions
A fraction is a part of whole. There are two numbers to every fraction, which are called term. A line separates the two terms. Number above the line is called numerator and the number below the line is called denominator. Denominator of a fraction tells us how many parts the whole is divided into and the numerator tells us how many parts are taken out the whole. For example, in the fraction\[\frac{2}{5}\], 5 is denominator. So, the whole unit or one whole has been cut into 5 equal parts.
![]()
2 is the numerator. Now, 2 parts out of 5 parts is being talked about or 1 part is going to be shaded or taken out. Here, the number \[\frac{2}{5}\] is known as fractional number and its symbol \[\frac{2}{5}\] is called a fraction.
Types of Fractions
There are several types of fractions. Let us study the fractions and their types.
Unit Fractions
A fraction, whose numerator is 1, is called a unit fraction. For example, \[\frac{1}{5},\frac{1}{3},\frac{1}{9},\frac{1}{10}\]are unit fractions. Here, the denominators of all fractions are different but numerators are 1.
Like and Unlike Fractions
Fractions in which the denominators are same, are called the like fractions and the fractions in which denominators are different, are called unlike fractions. For example, \[\frac{2}{3},\frac{1}{3},\frac{4}{3}\]are like fractions and \[\frac{2}{5},\frac{7}{4},\frac{3}{8}\] are unlike fractions.
Operations with Fractions
Addition of Like Fractions
Suppose two fractions are \[\frac{1}{5}\] and \[\frac{3}{5}\] and we have to add them.

So, we have, \[\frac{1}{5}+\frac{3}{5}=\frac{1+3}{5}=\frac{4}{5}\]
Therefore, the sum of like fractions \[=\frac{Sum\text{ }of\text{ }Numerators}{Common\text{ }Denominator}\]
Word Problems Based on Fractions
A fraction is defined as a portion of the whole. It is made up of two numbers: Numerator and Denominator. Fraction is a small amount of whole quantity. For example, if a piece of wire is divided into three parts, then each part is one-third part or \[\frac{1}{3}\] part of whole. The word problems involving fractions are usually based on real-life. Let us look at the following problems based on fractions.
Time and Clock
Time is important to plan our day. Time is the ongoing sequence of events. We use time to order events in the past, present and future. Time is passing non-stop. We use a clock or watch to measure time. Time is measured in seconds, minutes, hours, days, weeks, months and years with the help of clocks and calendars.
Indian Currency
Currency is a generally accepted form of money, including coins and paper notes. Different countries uses different currencies. Indian currency is know as Rupees. Symbol for Indian rupees is ‘Rs.’ and Symbol for Indian paise is 'p'. We write 78 rupees as Rs.78 and 50 paise as 50 p. There are 100 paise in one rupee. Suppose we have rupees one hundred four and twenty five paise. We can express the amount by using decimal notation also as Rs. 104.25. In India, the denominated coins are: 50 p, Rs. 1, Rs. 2, Rs. 5, Rs. 10, Rs. 20, Rs. 50, Rs. 100, Rs. 200, Rs. 500 and Rs. 2000. In International market, Indian rupees is known as INR (Indian Rupees).
Look at the following pictures of denominated Indian coins:





Paise 50 Rupee 1 Rupee. 2 Rupee. 5 Rupee. 10
Look at the following pictures of denominated Indian rupees:



Rs. 5 Rs. 10 Rs. 20



Rs. 50 Rs. 100


Rs. 500 Rs. 2000
Conversion of Rupees and False
As we know, 1 rupee is equal to 100 paise. Let us convert 350 paise into rupees. 350 paise = (100 + 100 + 100 + 50) paise
= (1 + 1 + 1) rupees + 50 paise = 3 rupees + 50 paise = 3.50 rupees
We can convert rupees and paise by multiplying and dividing also. Let us study the following rules.
Addition Involving Money
To add the given amount of money, steps are given below:
Step 1: First, express the given amount in figures and use dot (.) showing paise.
Step 2: Arrange the given amounts in a column in such a way that all the dots (.) fall in one column.
Step 3: Then, add the digits of amounts.
Step 4: Put the dot (.) in dot's column when the sum is obtained.
Step 5: Take the sum as amount.
Subtraction Involving Money
To subtract the given amount of money steps are given below:
Step 1: First, express the given amounts in figures and use dot (.) showing paise.
Step 2: Arrange the given amounts in a column in such a way that all the dots (.) fall in one column.
Step 3: Then, subtract the digits of amounts.
Step 4: Put the dot (.) in dot's column when the difference is obtained.
Step 5: Take the difference as amount.
Bills and Rate Charts
A bill is a written or printed statement showing how much money you one for goods or services. Bill is a very important part of buying and selling. Look at the following example. Priyanka went to a garment shop with her father. She bought the following items.
|
Garment Store |
||||
|
245, Bhikaji Cama Place, Delhi |
||||
|
Date: 25/07/2016 Bill no. 342 |
||||
|
S. No |
Item |
Rate per Item |
Rs. |
P |
|
1. |
2 Salwar |
500 |
1000 |
00 |
|
2. |
3 T-shirt |
200 |
600 |
00 |
|
3. |
1 Jacket |
700 |
700 |
00 |
|
4 |
2 Jeans |
800 |
1600 |
00 |
|
5. |
5 Pair of shoks |
40 |
200 |
00 |
|
|
|
Total |
4100 |
00 |
|
Signature of Shopkeeper |
|
|
|
|
Look at the bill prepared by the shopkeeper. Here, the shopkeeper made a proper bill mentioning the items bought, quantity and rates. Name and address of the shop, date of purchase, bill number, signature of the shopkeeper all these are parts of a bill. The bill shown above contains everything that is required. Let us look at the following examples based on bills and rate charts.
Word Problems Involving Money
In this section, we will solve the word problems involving money which include addition and subtraction. Let us study the following examples.
What is Unitary Method
Unitary method is also known as method of one. The term 'Unitary Method' is a technique which has evolved from the concept of 'unit' which means 'of one'.
In Unitary Method:
Rules Applied in Unitary Method
Rule 1: If we know the value of one, then to find the value of many, we do multiplication.
Rule 2: If we know the value of many, then to find the value of one, we do division.
Rule 3: If we know the value of many, then to find the value of more than given or less than given, we first need to calculate the value of one.
Problems Based on Unitary Method
Some examples of problems based on unitary method are given below. Let us study the following examples.
Example-1
1. Which of the following shows 4 equal parts of whole?
(a)  (b)
(b) 
(c) 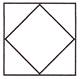 (d)
(d) 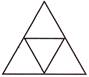
(e) None of these
Answer (d) is correct.
Explanation: Figure given in option (d) has four equal parts. Figures given in other options do not have equal parts.
Rest of the options is incorrect because of the correctness of option (d).
2. In which of the following figures, the fraction represented by shaded circles is equal to\[\frac{1}{5}\]?
(a)  (b)
(b) 
(c)  (d)
(d) 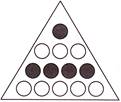
(e) None of these
Answer (b) is correct.
Explanation: In option (a), denominator of the fraction represented by shaded circles\[=12\div 4=3\]. Therefore, fraction \[=\frac{1}{3}\]
In option (b), denominator of the fraction represented by shaded circles\[=10\div 2=5\]. Therefore, fraction\[=\frac{1}{5}\]
In option (c), denominator of the fraction represented by shaded circles\[=10\div 5=2\]. Therefore, fraction\[=\frac{1}{2}\]
In option (d), denominator of the fraction represented by shaded circles\[=15\div 5=3\]. Therefore, fraction \[=\frac{1}{3}\]
Rest of the options is incorrect because of the correctness of option (b).
3. In which of the following figures, the fractions represented by the shaded parts are like fractions?
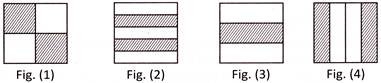
(a) Fig. (2) and fig. (3) (b) Fig. (1) and fig. (4)
(c) Fig. (1) and fig. (3) (d) Fig. (2) and fig. (3)
(e) None of these
Answer (b) is correct.
Explanation: Fraction represented by the shaded parts in Fig. (1) \[=\frac{2}{4}\]
Fraction represented by the shaded parts in Fig. (2) \[=\frac{2}{5}\]
Fraction represented by the shaded parts in Fig. (3) \[=\frac{1}{3}\]
Fraction represented by the shaded parts in Fig. (4) \[=\frac{2}{4}\]
Thus, in Fig. (1) and Fig. (4), the fractions represented by shaded parts are like fractions.
Rest of the options is incorrect because of the correctness of option (b).
4. Which one of the following sets is a set of equivalent fractions?
(a) \[\frac{3}{4},\frac{4}{6},\frac{5}{2},\frac{8}{9}\] (b) \[\frac{3}{4},\frac{6}{8},\frac{9}{12},\frac{12}{16}\]
(c) \[\frac{1}{3},\frac{3}{4},\frac{2}{6},\frac{6}{8}\] (d) \[\frac{2}{8},\frac{3}{9},\frac{8}{16},\frac{4}{12}\]
(e) None of these
Answer (b) is correct.
Explanation: Here, the set of fractions given in option (b) is the set of equivalent fractions, which are \[\frac{3}{4},\frac{6}{8},\frac{9}{12},\frac{12}{16}\] because,
\[\frac{3}{4}=\frac{3}{4},\frac{6}{8}=\frac{6\div 2}{8\div 2}={{\frac{3}{4}}_{\,,\,}}\frac{9}{12}=\frac{9\div 3}{12\div 3}=\frac{3}{4},\frac{12}{16}=\frac{12\div 4}{16\div 4}=\frac{3}{4}\]
Rest of the options is incorrect because of the correctness of option (b).
5. Which one of the following sets of figures shows \[\frac{3}{4}>\frac{2}{4}\] with respect to the fraction represented by shaded parts?
(a) 
(b) 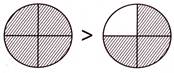
(c) ![]()
(d) 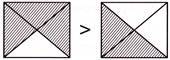
(e) None of these
Answer (d) is correct.
Explanation: In option (a), for the fractions represented by shaded parts,\[\frac{2}{4}>\frac{1}{4}\]
In option (b), for the fractions represented by shaded parts,\[\frac{4}{4}>\frac{3}{4}\]
In option (c), for the fractions represented by shaded parts,\[\frac{4}{4}>\frac{2}{4}\]
In option (d), for the fractions represented by shaded parts,\[\frac{3}{4}>\frac{2}{4}\]
Rest of the options is incorrect because of the correctness of option (d).
6. Which of the following sets of fractions are arranged from the largest to the smallest?
(a) \[\frac{1}{4},\frac{2}{4},\frac{3}{4},\frac{6}{4},\frac{10}{4}\] (b) \[\frac{18}{9},\frac{16}{9},\frac{11}{9},\frac{4}{9},\frac{1}{9}\]
(c) \[\frac{18}{3},\frac{10}{3},\frac{6}{3},\frac{11}{3},\frac{13}{3}\] (d) \[\frac{12}{6},\frac{8}{6},\frac{9}{6},\frac{3}{6},\frac{4}{6}\]
(e) None of these
Answer (b) is correct.
Explanation: As we know, if the denominators of the fractions are same, then the bigger fraction has the larger numerator. Here, in option (b),
18>16>11>4>1. Therefore, \[\frac{18}{9}>\frac{16}{9}>\frac{11}{9}>\frac{4}{9}>\frac{1}{9}\]
Or, in descending order, it is; \[\frac{18}{9},\frac{16}{9},\frac{11}{9},\frac{4}{9},\frac{1}{9}\]
Rest of the options is incorrect because of the correctness of option (b).
Common Asked Question
1. In which one of the following figures, the fraction represented by shaded parts is\[\frac{1}{4}\]?
(a) 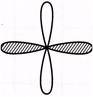 (b)
(b) 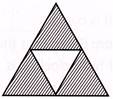
(b) ![]() (d)
(d) 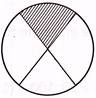
(e) None of these
2. Kanika said that the time is 9:30 in her clock. Which of the following clocks is Kanika's clock?
(a)  (b)
(b) 
(c)  (d)
(d) 
(e) None of these
Answer (c) is correct.
Explanation: Time shown by clock given in option (c) is 9:30 because its minute hand is at 6 which shows 30 minutes and its hour hand is at 9.
Rest of the options is incorrect because of the correctness of option (c).
3. In a mathematics test paper, the maximum time to solve the paper is 45 minutes. If the test starts at 10: 55 am, at what time does it end?
(a) 9: 40 am (b) 11: 40 am
(c) 11: 50 am (d) 11: 30 am
(e) None of these
Answer (b) is correct.
Explanation: Given that the test starts at 10: 55 am.
Now in 24-hour clock, it is 10: 55 hours.
So, the maximum time for the test = 45 minutes
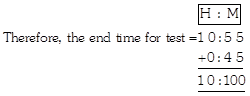
Or, end time = 10:100 = (10 + I): (100 - 60) am = 11: 40 am
So, at 11: 40 am the test will end.
Rest of the options is incorrect because of the correctness of option (b).
4. In a mathematics test paper, the maximum time to solve the paper is 45 minutes. If the test starts at 10: 55 am, at what time does it end?
(a) 9: 40 am (b) 11: 40 am
(c) 11: 50 am (d) 11: 30 am
(e) None of these
Answer (b) is correct.
Explanation: Given that the test starts at 10: 55 am.
Now in 24-hour clock, it is 10: 55 hours.
So, the maximum time for the test = 45 minutes
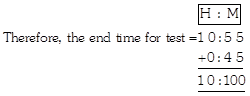
Or, end time = 10:100 = (10 + I): (100 - 60) am = 11: 40 am
So, at 11: 40 am the test will end.
Rest of the options is incorrect because of the correctness of option (b).
5. Rahul's birthday falls on the day just before 3rd Monday of the April 20XX. When is Rahuls birthday?
|
April 20XX |
||||||
|
S |
M |
T |
W |
T |
F |
S |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
7 |
8 |
9 |
10 |
11 |
12 |
13 |
|
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
21 |
22 |
23 |
24 |
25 |
26 |
26 |
|
28 |
29 |
30 |
|
|
|
|
(a) April 18, 20XX
(b) April 14, 20XX
(c) April 15, 20XX
(d) April 16, 20XX
(e) None of these
Answer (b) is correct.
Explanation: Date on 3rd Monday of the April 20XX is April 15, 20XX.
Date one day before April 15, 20XX is April 14, 20XX.
Therefore, Rahul birthday falls on April 14, 20XX.
Rest of the options is incorrect because of the correctness of option (b).
6. Peter is making the calendar for bulletin board as shown below. Which day of I the week will be on March 17, 20XX?
|
March 20XX |
||||||
|
Sun |
Mon |
Tue |
Wed |
Thu |
Fri |
Sat |
|
|
|
|
1 |
2 |
3 |
4 |
|
5 |
6 |
7 |
8 |
9 |
10 |
11 |
(a) Thursday (b) Wednesday
(c) Friday (d) Saturday
(e) None of these
Answer (c) is correct.
Explanation: As we know, after seven days, days repeat. Here, 17 = 7 + 7 + (3)
Now, day on March 3, 20XX is Friday. And, day on March 10, 20XX is Friday.
So, day on March 17, 20XX is also Friday.
Rest of the options is incorrect because of the correctness of option (c).
7. Ankita went to a stationary shop. She bought the things shown below. How much she has to pay?

(a) Rs. 98.75 (b) Rs. 96.25
(c) Rs. 97.65 (d) Rs. 95.35
(e) None of these
Answer (b) is correct.
Explanation: Here, the cost of Notebook = Rs. 40.50
The cost of Instrument box = Rs. 55.75
Now, addition is as fallow:
Therefore, Ankita has to pay the sum amount = Rs. 96.25
Rest of the options is incorrect because of the correctness of option (b).
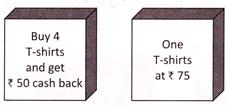
8. If Rahul bought five T-shirts at the price shown below, then how much he has to pay including the given offer?
(a) Rs. 450 (b) Rs. 325
(c) Rs. 375 (d) Rs. 350
(e) None of these
Answer (b) is correct.
Explanation: Since, Rahul bought five T-shirts at Rs.75.
Therefore, the cost of 5 T-shirts \[=Rs.75+Rs.75+Rs.75+Rs.75+Rs.75=Rs.375\]
Now, given offer is Rs.50 cashback on buying 4 T-shirts.
Therefore, Rahul has to pay including given offer \[=Rs.375-Rs.50=Rs.325\]
Rest of the options is incorrect because of the correctness of option (b).
9. This is a box of chocolates. Which of the following statements hold true from the given information.
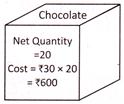
(a) It contains 20 chocolates.
(b) Each chocolate costs Rs. 600.
(c) Cost of 20 chocolates = Rs. 50.
(d) All chocolates are of different cost.
(e) Cannot be determined
Answer (a) is correct.
Explanation: All information given on the box of chocolate is as follows:
(1) It contains 20 chocolates.
(2) Each chocolate costs Rs. 30.
(3) Cost of 20 chocolates is Rs. 600.
(4) All chocolates are of same cost.
Therefore, the information given in option (a) is correct
Rest of the options is incorrect because of the correctness of option (a).
10. Mohit bought these four things
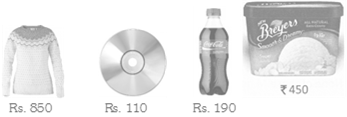
What was the total cost of these four items?
(a) Rs. 1500 (b) Rs. 1550
(c) Rs. 1600 (d) Rs. 1750
(e) None of these
Answer (c) is correct.
Explanation: Total cost of the given four items \[=850+110+190+450=1600\]
Rest of the options is incorrect because of the correctness of option (c).
11. If the price of one bicycle is Rs. 1200, then what is the price of such 5 bicycles?
(a) Rs. 1700 (b) Rs. 4000
(c) Rs. 5600 (d) Rs. 6000
(e) None of these
Answer (d) is correct.
Explanation: Here, price of one bicycle is Rs. 1200 and we have to find out the price of 5 such bicycles. Therefore, we multiply the price of 1 bicycle by 5.
Hence, the price of 1 bicycle = Rs. 1200
So, the price of 5 bicycles\[=Rs.(1200\times 5)=Rs.6000\]
Rest of the options is incorrect because of the correctness of option (d).
12. If the cost of 2 apples is Rs. 24, then find the cost of 3 such apples.
(a) Rs.36 (b) Rs.42
(c) Rs.32 (d) Rs.27
(e) None of these
Answer (a) is correct.
Explanation: As the cost of 2 apples = Rs. 24
Therefore, the cost of 1 apple \[=\text{ }Rs.24\div 2=Rs.12\]
So, the cost of 3 apples \[=Rs.\left( 12\times 3 \right)=Rs.36\]
Rest of the options is incorrect because of the correctness of option (a).
13. If 4 litres of petrol is consumed by a car in covering a distance of 80 km, then how many kilometres will it go in 5 litres of petrol?
(a) 140 km (b) 90 km
(c) 100 km (d) 120 km
(e) None of these
Answer (c) is correct.
Explanation: As we know, if the value of many is given, then to find out the value of more than given or less than given, we first need to calculate the value of one.
Here, in 4 litres of petrol, the car covered the distance = 80 km
Therefore, in 1 litre of petrol, the car will cover the distance
\[=\left( 80\div 4 \right)km=20km\]
So, in 5 litres of petrol, the car will cover the distance \[=\text{ }\left( 20\times 5 \right)\text{ }km\text{ }=\text{ }100\text{ }km\]
Rest of the options is incorrect because of the correctness of option (c)
14. If the cost of 10 kilograms of rice is Rs. 90, then what is the cost of 560 kilograms of rice?
(a) Rs. 5400 (b) Rs. 5040
(c) Rs. 4050 (d) Rs. 4500
(e) None of these
Answer (b) is correct.
Explanation: Here, to find out the value of more than given or less than given, first we need to find out the value of one.
Since, the cost of 10 kilograms of rice = Rs. 90
So, the cost of 1 kilogram of rice \[=\text{ }Rs.90\div 10=Rs.9\]
Therefore, the cost of 560 kilograms of rice \[=Rs.\left( 9\times 560 \right)=Rs.5040\]
Rest of the options is incorrect because of the correctness of option (b).
15. If ![]() represents 4 items, and the cost of
represents 4 items, and the cost of ![]() = Rs. 72, then the cost of
= Rs. 72, then the cost of ![]()
![]() will be:
will be:
(a) Rs. 42 (b) Rs. 54
(c) Rs. 48 (d) Rs. 60
(e) None of these
Answer (c) is correct
Explanation: Given that ![]() represents 4 items.
represents 4 items.
Therefore, ![]() represent \[\left( 4\times 6 \right)\] items = 24 items
represent \[\left( 4\times 6 \right)\] items = 24 items
And, ![]() represent \[\left( 4\times 4 \right)\] items = 16 items
represent \[\left( 4\times 4 \right)\] items = 16 items
Now, the cost of 24 items = Rs. 72
So, the cost of 1 item\[=Rs.(72\div 24)=Rs.3\]
Therefore, the cost of 16 items\[=Rs.\left( 3\times 16 \right)=Rs.48\]
Hence, the cost of ![]() is Rs. 48
is Rs. 48
Rest of the options is incorrect because of the correctness of option (c).
16. If cost of half dozen guavas is Rs. 72, then find the cost of 9 such guavas.
(a) Rs. 108 (b) Rs. 96
(c) Rs. 60 (d) Rs. 84
(e) None of these
Answer (a) is correct.
Explanation: Half dozen = 6. As the cost of half dozen guavas = Rs. 72
So, the cost of 6 guavas = Rs. 72
Therefore, the cost of 1 guava \[=Rs.\left( 72\div 6 \right)=Rs.12\]
Hence, the cost of 9 guavas \[=Rs.\left( 12\times 9 \right)=Rs.108\]
Rest of the options is incorrect because of the correctness of option (a).
You need to login to perform this action.
You will be redirected in
3 sec
