Measurement
Category : 3rd Class
Measurement
Learning Objectives
Introduction
The act or process of measuring something is called measurement. Measurement is the elementary information about everything. Length, width, height and capacity (volume) of a thing are measured in appropriate units. In this chapter, we will learn about the concept of measurement.
Units of Measurement
The metric system was introduced to measure length, mass (weight) and capacity (volume). The modern form of the metric system is known as SI Unit or the International
System of Units.
|
SI units or Base Units |
|
|
Physical Qualities |
SI Unit |
|
Length |
Metre (m) |
|
Mass |
Kilometre (kg) |
|
Time |
Second (s) |
Some units of measurement obtained by multiplication or division of the SI units and are called derived units. For example, unit of speed is metre per second (m/s) or kilometre per hour (km/ h) is a derived unit.
Measurement of Length and Distance
The shape and size of everything is measured by a measuring instrument. Rulers are well known devices for the Measurement of length. Measured lengths are expressed in units. The units for measured lengths are kilometre (km), metre (m), centimetre (cm) and millimetre (mm). Small lengths are measured in metre, centimetre and millimertre. The length of our one finger is measured in inches, centimetres or in millimetres but the distance between two cities is measured in kilometres. The standard unit used to measure any length or distance is the metre for which we use W. To convert metres into centimetres, we multiply metre by 100, therefore, 100 cm = 1 m. To convert kilometres into metres, we multiply kilometre by 1000, thus 1000 m = 1 Kilometre.
|
Conversion Table for Length and Distance |
|
|
10 millimetres (mm) |
1 centimetres (cm) |
|
10 centimetres (cm) |
1 decimetres (dm) |
|
10 decimetres (dm) |
1 metres (m) |
|
10 metres (m) |
1 decametres (dam) |
|
10 decametres (dam) |
1 hectometres (hm) |
|
10 hectometres (hm) |
1 kilometre (km) |
Operations with Measured Lengths
Addition of Measured Lengths with Conversion
Following steps are used for the addition of measured lengths:
Step 1: Convert the metres into centimetres if the given lengths are in metres and centimetres.
Step 2: Add the centimetres.
Step 3: Convert the sum back to metres.
Multiplying the Measured Length
Following steps are used for multiplying the measured length:
Step 1: Arrange the numbers in metres (m) and centimetres (cm) columns if the given length is in metres and centimetres.
Step 2: Multiply the numbers by given multiplier.
Step 3: Product so obtained is the required length.
Measurement of Mass
The standard unit for the measurement of mass is kilogram (kg). The other units for measuring mass are grams (g) and milligrams (mg). Mass of small things is usually measured in grams. To convert kilograms into grams, we multiply kilogram by 1000, therefore, one gram is thousandth part of a kilogram.
|
Conversion Table for Mass |
|
|
10 milligrams (mg) |
1 centigrams (cg) |
|
10 centigrams (cg) |
1 decigram (dg) |
|
10 decigram (dg) |
1 grams (g) |
|
10 grams (g) |
1 decagrams (dag) |
|
10 decagrams (dag) |
1 hectogram (hg) |
|
10 hectogram (hg) |
1 kilogram (kg) |
Operations with Measured Masses
Addition of Measured Masses with Conversion
Following steps are used for the addition of measured masses:
Step 1: Convert the kilograms into grams if the given masses are in kilograms and grams.
Step 2: Add the grams.
Step 3: Convert the sum back to kilograms.
Measurement of Capacity (Volume)
The capacity of a container is the maximum quantity of liquid that container can contain. If the capacity of a container is 1 litre then it means, it can hold the volume 1 litre of liquid inside it. The standard unit for the measurement of liquid is litre. The larger volume of liquid is measured in litres and the smaller volume is in millilitres. One litre is equal to 1000 millilitres. Therefore, one millilitre is the thousanth part of a litre, litre is denoted by letter of English alphabet (l) or (L) and millilitre is denoted by (ml).
|
Conversion Table for Capacity |
|
|
10 millilitres (ml) |
1 centilitre (cl) |
|
10 centilitres (cl) |
1 decilitres (dl) |
|
10 decilitres (dl) |
1 litres (l) |
|
10 litres (l) |
1 decalitres (dal) |
|
10 decalitres (dal) |
1 hectolitres (hl) |
|
10 hectolitres (hl) |
1 kilolitre (kl) |
Operations with Measured Capacities
Addition of Measured Capacities with Conversion
Following steps are used for the addition of measured capacities:
Step 1: Convert the litres in millilitres if the given capacities are in litres and millilitres.
Step 2: Add the millilitres.
Step 3: Convert the sum back to litres.
Example-1
1. Distance between two colonies in a city is 15 km 540 m. Express the distance in metres.
(a) 14460 m (b) 15540 m
(c) 15054 m (d) 54015 m
(e) None of these
Answer (b) is correct.
Explanation: \[15\text{ }km\text{ }540\text{ }m\text{ }=\left( 15\times 1000 \right)\text{ }m+540\text{ }m=\left( 15\times 1000+540 \right)\text{ }m\]\[=\left( 15000+540 \right)m\text{ }=15540\text{ }m\].
Rest of the options is incorrect because of the correctness of option (b).
2. Add 48 m 65 cm and 83 m 70 cm.
(a) 134m 45 cm (b) 132 m 61 cm
(c) 132m 35 cm (d) 98 m 41 cm
(e) None of these
Answer (c) is correct.
Explanation: Here, addition is as follow:
Therefore, the required sum is 132 m 35 cm.
Rest of the options is incorrect because of the correctness of option (c).
3. Find the one-fourth part of 39 L 180 ml.
(a) 9 L 795 ml (b) 8 L 45 ml
(c) 9 L 245 ml (d) 7 L 885 ml
(e) None of these
Answer (a) is correct.
Explanation: One-fourth part means division by 4. Here, division is as follows:
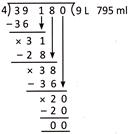
Therefore, one-fourth part of the given capacity is 9 L 795 ml.
Rest of the options is incorrect because of the correctness of option (a).
4. Maria has a rope 7 m 35 cm long and Jenny has another rope 8 m 80 cm long. What is the total length of both ropes?
(a) 15 m 45 cm (b) 16 m 15 cm
(c) 15 m 95 cm (d) 16 m 95 cm
(e) None of these
Answer (b) is correct.
Explanation: Here, addition is as follows:
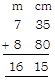
Therefore, total length of both the ropes is 16 m 15 cm.
Rest of the options is incorrect because of the correctness of option (b).
5. Peter travels 6 km 200 m by bus and 2 km 850 m by auto to reach the school from his house. How far is Peter's school from his home?
(a) 8 km 950 m (b) 9 km 50 m
(c) 9 km 500 m (d) 8 km 50 m
(e) None of these
Answer (b) is correct.
Explanation: On adding the both distances, we get 6 km 200 m + 2 km 850 m
= 6000 m + 200 m + 2000 m + 850 m = 9050 m = 9 km 50 m
Therefore, Peter's school from his home is at 9 km 50 m. .
Rest of the options is incorrect because of the correctness of option (b).
Common Asked Question
1. An electrician needs 14 m 25 cm of electric wire for internal wiring of a room. How much long wire does he need for internal wiring of 5 such rooms?
(a) 71 m 25 cm (b) 70 m 75 cm
(c) 72m 25 cm (d) 69 m 75 cm
(e) None of these
Answer (a) is correct.
Explanation: Here, multiplication is as follows:
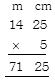
When 14 m 25 cm is multiplied by 5, the product is 71 m 25 cm.
Therefore, the required length of wire is 71 m 25 cm
Rest of the options is incorrect because of the correctness of option (a).
2. What should be subtracted from 53 kg 410 g to get 35 kg 140 g?
(a) 18 kg 270 g (b) 16 kg 390 g
(c) 17 kg 550 g (d) 19 kg 720 g
(e) None of these
Answer (a) is correct.
Explanation: As we know, subtraction is the inverse process of addition. Here, subtraction is as follows:

Therefore, 18 kg 270 g should be subtracted from 53 kg 410 g to get
35 kg 140 g.
Rest of the options is incorrect because of the correctness of option (a).
3. If ![]() = 750 ml, then what is the capacity of
= 750 ml, then what is the capacity of ![]() ?
?
(a) 6 L (b) 3 L
(c) 4.5 L (d) 3.5 L
(e) None of these
Answer (b) is correct.
Explanation: Here, the capacity of ![]() = 750 ml
= 750 ml
So, the capacity of 4 such cups \[=\text{ }\left( 750\times 4 \right)ml\text{ }=\text{ }3000\] ml. Now, 1000 ml = 1 L
Or, \[3000\text{ }ml\,=\left( \frac{1}{1000}\times 3000 \right)L=3\text{ }L\]
Rest of the options is incorrect because of the correctness of option (b).
4. If ![]() = 180 grams, then
= 180 grams, then![]()
(a) 72 grams (b) 68 grams
(c) 84 grams (d) 90 grams
(e) None of these
Answer (a) is correct.
Explanation: Given that the weight of 5 balls = 180 grams
Or, the weight of 1 ball \[=\left( 180\div 5 \right)\] grams = 36 grams
Therefore, the weight of \[2\text{ }balls=\left( 36\times 2 \right)\] grams = 72 grams
Rest of the options is incorrect because of the correctness of option (a)
You need to login to perform this action.
You will be redirected in
3 sec
