Number System
Category : 3rd Class
Number System
Learning Objectives
Types of Number
Numbers are classified according to their types. The first type of numbers is the counting numbers or the natural numbers and the next type of numbers is the whole numbers, which are the natural numbers together with zero. Let us study these two number types.
Natural Numbers and Whole Numbers
Natural Numbers
Counting numbers are known as natural numbers. There are infinite natural numbers starting from 1. Natural numbers are denoted by N. Therefore,
N = {1, 2, 3, 4,.....}
![]()
The arrow-head on the right side shows the natural numbers counting upto infinite.
Whole Numbers
Counting numbers including 0 are known as whole numbers. If the counting numbers start from 0, then they include the set of whole numbers. Whole numbers are denoted by W. Therefore,
W= {0, 1, 2, 3, 4, 5,......}
![]()
The arrow-head on the right side shows the whole numbers counting up to infinite.
Ascending and Descending Order
Ascending Order
Numbers in a group are said to be in ascending order when they are arranged from the« smallest to the largest number. For example, the ascending order of the numbers: 45, 23, 34, 76, 87, 90 is 23 < 34 < 45 < 76 < 87 < 90.
Descending Order
Numbers in a group are said to be in descending order when they are arranged from the largest to the smallest. For example, the descending order of the number: 56, 34, 46, 23, 55 is\[56>55>46>34>23\].
Face Value and Place Value
We have already learnt about ones, tens and hundreds upto three places. Now, we will learn about the fourth place which is 'thousands' or 1000s. A number with thousands place will have four digits in it.
Face Value of a Digit
The face value of a digit in a number is the value of the digit itself. Therefore, the face value of a number does not change on changing its place. For example, in the number 4673, the face value of 6 is 6. If the digit 6 changes its place from hundreds to tens (4763), then the face value of 6 remains same as 6.
Place value of a Digit
The place value of a digit is the value of where the digit is in the number. The place value of a number changes according to the placement of digits in the number. The place value of 6 in the number 4673 is 600. On changing the place of 6 from 4673 to 4763, the place value of 6 changes from 600 to 60.
Number Facts
Number Patterns
Pattern means repetition. We can create pattern with numbers too. A number pattern is a list of numbers that follows a certain rule, sequence or pattern. Look at the following number pattern:
1, 5, 9, 13, 17
He re, starting from 1, every alternate number is a part of this pattern. When we observe this number pattern, we find that4 is added each time to get the next term of the pattern.
Problems Based on Numbers
Number word problems is a mathematical exercise based on numbers and to solve these problems, we extract the Maths from English text. Look at the following examples based on numbers.
An Introduction to Roman Numerals
Numeral is a symbol or name used to represent a number. We use Hindu-Arabic numerals in which there are ten symbols 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9. Ancient Romans used a special method of showing numbers. Roman numerals are represented by seven different letters: I, V, X, L, C, D and M, where I = 1, V = 5, X= 10, L = 50, C= 100, D = 500 and M = 1000. We use these seven letters to make thousands of different numbers. For example, we write 9 = IX, 13 = XIII, 56 = LVI and 115 = CXV, etc. We will study Roman numerals in details in the next class.
Addition
Addition is bringing two or more numbers (or things) together to make a new total. The numbers which are added to each other are called addends and the result is called sum. For example, in 456 + 567 = 1023, the numbers 456 and 567 are addends and the resulting number 1023 is their sum. The process of addition of the numbers always starts from ones place digit. Other names use for addition are: plus, increase, total and sum. The term used for addition is 'plus' and the symbol for plus is '+'
Subtraction
Subtraction is the inverse process of addition. Subtraction is taking one number (or thing) away from another. It is a method by which we know the remaining after taken away some quantity from a certain quantity. Number which is subtracted is called subtrahend and the number from which we subtract is called minuend. The number left after subtraction is called the difference.
For example, in the subtraction, 29 - 14 = 15, the number 14 is subtrahend and 29 is minuend. The result 15 is the difference of 29 and 14.
The process of subtraction of the numbers always starts from ones place digits.
Number Sentence
A number sentence is a group of numbers that includes a mathematical operation: addition, subtraction, multiplication or division.
Word Problems Based on Addition and Subtraction
The key words used in problems involving addition are: sum, total, in all, all together, altogether, etc. The key words used in problems involving subtraction are: take away, how many more, how many less, smaller than, greater than etc. Let us see the following examples based on addition and subtraction.
Multiplication
Multiplication means repeated addition. It is a faster way of adding the same number. When thinking of multiplication as repeated addition, the multiplication of two whole numbers is equal to adding as many copies of one of them. For example, the product 5 x 4 is equal to the sum of four 5's, or, 5 + 5 + 5 + 5. When a quantity is added to itself number of times, we use operation of multiplication to find the resulting quantity. In a multiplication, the number which is multiplied is called multiplicand. The number by which the multiplicand is multiplied is called multiplier. The answer or the result of multiplication is called its product. The term used for multiplication is 'multiply by' and the symbol for multiplication is (x).
Division
Division means repeated subtraction of the same number. It is splitting into equal parts or groups. It is the inverse process of multiplication. It determines the one value is how many times one value is greater than the another value. In a division, the number to be divided is called the dividend. The number by which division is made is called .the divisor. The number of groups we get is called the quotient. The leftover is .called the remainder. In a division, we always have:
\[\mathbf{Dividend=}\left( \mathbf{Divisor\times Quotient} \right)\mathbf{+Remainder}\]
The term used for division is "divided by" and the symbol for division is (-).
Division as Repeated Subtraction
Division can be seen as repeated subtraction. Let us see the following example where 15 is divided by 5.
![]()
Here, 5 is subtracted 3 times till we get 0. So, 15 - 5 - 5 - 5 = 0
Divisibility Rules and Division Facts
Divisibility Rules
A divisibility test is a rule for determining whether one whole number is divisible by another without leaving remainder.
Problems Based on Multiplication and Division
Multiplication is the expanded form of addition and division is the inverse of multiplication. Let us see the following examples based on multiplication and division.
Example-1
1. Difference between the face value and place value of 3 in the number 4312 is:
(a) 300 (b) 297
(c) 2997 (d) 27
(e) None of these
Answer (b) is correct.
Explanation: In the given number 4312, the place value of 3 is 300 and its face value is 3.
Therefore, the required difference \[=300-3=297\]
Rest of the options is incorrect because of the correctness of option (b).
2. Which one of the following is the expanded form of 7206?
(a)\[7000+20+6\] (b) \[700+200+6\]
(c)\[7000+200+6\] (d) \[7000+200+60\]
(e) None of these
Answer (c) is correct.
Explanation: Expanded form of 7206 is \[7000+200+6\].
Rest of the options is incorrect because of the correctness of option (c).
3. How many hundreds are there in 7329?
(a) 3 (b) 30
(c) 2 (d) 7
(e) None of these
Answer (a) is correct.
Explanation: Here, \[7329=7000+300+20+9=7000+(3\times 100)+20+9\]
Clearly, there are 3 hundreds in the number 7329.
Rest of the options is incorrect because of the correctness of option (a).
4. Garima has Rs. 1349. Which of the following is the correct number name for 1349?
(a) One thousand four hundred thirty nine
(b) One thousand three hundred forty nine
(c) One thousand thirty four hundred
(d) One thousand four thirty nine
(e) None of these
Answer (b) is correct.
Explanation: Here,\[1349=1000+300+40+9\]
So, 1349 = One thousand three hundred and forty nine
Rest of the options is incorrect because of the correctness of option (b).
5. Which of the following has the place value of 3 as 300?
(a) 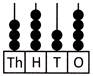 (b)
(b) 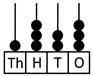
(c) 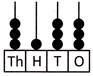 (d)
(d) 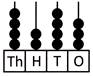
(e) None of these
Answer (b) is correct.
Explanation: On the abacus given in option (b), there are 3 beads on its hundreds place column. Therefore, the place value of 3 as 300 is shown by the abacus given in option (b).
Rest of the options is incorrect because of the correctness of option (b).
Common Asked Question
1. Rekha, Garima, Monika and Sumita are playing a number game. Each of them are writing their favourite number. Who wrote the greatest number?
![]()
(a) Sumita (b) Monika
(c) Rekha (d) Garima
(e) None of these
Answer (c) is correct.
Explanation: Here, Rekha wrote 7532 and Monika wrote 7325. Both numbers have 7 at thousands place but at hundreds place, 5 > 3. Therefore, 7532 is the greatest number of all four written numbers.
Rest of the options is incorrect because of the correctness of option (c).
2. Which of the following sets of the numbers is in descending order?
(a) 3526, 3915, 3312, 3419
(b) 5581, 5518, 5185, 5815
(c) 2901, 2894, 2848, 2839
(d) 7356, 7536, 7635, 7736
(e) None of these
Answer (c) is correct.
Explanation: Set of numbers given in option (c) is: \[2901,\text{ }2894,\text{ }2848,\text{ }2839\]
Where,\[~2901>2894>2848>2839\] , which is in descending order.
Rest of the options is incorrect because of the correctness of option (c).
3. 8215 is same as:
(a)\[8000+200+10+5\] (b) \[800+20+15\]
(c)\[8000+210+50\] (d) \[800+200+10+5\]
(e) None of these
Answer (a) is correct.
Explanation: 8215 in expanded form is\[\left( 8000+200+10+5 \right)\].
Rest of the options is incorrect because of the correctness of option (a).
Which one of the following numbers will replace the question mark (?) in the number pattern given below?
4. 10, 30, 20, 40, 30, 50, ?
(a) 40 (b) 30
(c) 60 (d) 70
(e) None of these
Answer (a) is correct.
Explanation: Given number pattern is: 10, 30, 20, 40, 30, 50, ...... Rule followed:
![]()
Therefore, the required missing number = 40
Rest of the options is incorrect because of the correctness of option (a).
5. Successor of the largest 4-digit number is:
(a) the largest 4-digit number.
(b) the smallest 4-digit number.
(c) the largest 5-digit number.
(d) the smallest 5-digit number.
(e) None of these
Answer (d) is correct.
Explanation: The largest 4-digit number = 9999. Successor of\[9999=9999+1=10000\]; which is the smallest 5-digit number.
Rest of the options is incorrect because of the correctness of option (d).
6. Which one of the following is not true?
(a) \[271+0=271\] (b) \[271-0=271\]
(c) \[0+271=271\] (d) \[0-271=271\]
(e) None of these
Answer (d) is correct.
Explanation: Here, \[271+0=271\](Additive Property of Zero), \[0+271=271\]
(Additive Property of Zero), \[271-0=271\](Additive Property of Subtraction) but \[\left( 0-271 \right)\] is not defined.
Rest of the options is incorrect because of the correctness of option (d).
7. Which one of the following numbers will replace the question mark (?) in the number sentence given below?
\[137-49=24+\]
(a) 65 (b) 64
(c) 62 (d) 63
(e) None of these
Answer (b) is correct.
Explanation: Here, \[137-49=88\]. Now, \[24+=88\].
As we know, subtraction is the inverse process of addition.
Therefore, 88 - 24. So, we have, \[24+=88\].
Or, the required missing number is 64.
Rest of the options is incorrect because of the correctness of option (b).
8. If ![]() = 3215 and
= 3215 and ![]() = 5427, then the value of
= 5427, then the value of ![]() will be:
will be:
(a) 2392 (b) 2212
(c) 3462 (d) 4622
(e) None of these
Answer (b) is correct.
Explanation: Here, given that
![]() = 3215 and
= 3215 and ![]() = 5427
= 5427
Or, 3215+ ![]() = 5427
= 5427
As we know, subtraction is the inverse process of addition.
Therefore, difference of 5427 and 3215 is \[5427-3215=2212\]
So, we have, \[3215+\] ![]() 5427 or, \[3215+2212=5427\]
5427 or, \[3215+2212=5427\]
Or, ![]() =2212.
=2212.
Rest of the options is incorrect because of the correctness of option (b).
9. Which one of the following numbers will replace the question mark \[\] in the subtraction given below?
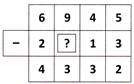
(a) 6 (b) 5
(c) 4 (d) 7
(e) None of these
Answer (a) is correct.
Explanation: Here, subtraction is as follow:
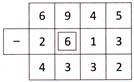
Clearly, at the hundreds place in \[2,\text{1}3,\] the missing digit is \[9-=3\] or, \[3+=9\]. So, the required missing digit is
Rest of the options is incorrect because of the correctness of option (a).
10. The cost difference of 1 pen and 1 pencil is Rs. 7. If the cost of 1 pencil is Rs. 3, then the cost of 1 pen will be:
(a) Rs. 5 (b) Rs. 10
(c) Rs. 9 (d) Rs. 11
(e) None of these
Answer (b) is correct.
Explanation: Here, the cost of 1 pencil = Rs. 3, and the cost difference = Rs. 7
Therefore, the cost of 1 pen = cost of 1 pencil + cost difference = Rs. (3 + 7) = Rs. 10
Rest of the options is incorrect because of the correctness of option (b).
11. If ![]() =7215 and
=7215 and ![]() = 2946, the value of
= 2946, the value of ![]() is:
is:
(a) 3849 (b) 4479
(c) 4269 (d) 5219
(e) None of these
Answer (c) is correct.
12. Find the sum of missing two digits \[\] in the subtraction given below.
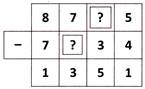
(a) 12 (b) 11
(c) 13 (d) 14
(e) None of these
Answer (a) is correct.
Explanation: Here, the subtraction is as follow:
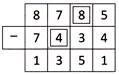
Therefore, the required sum of missing digits = 4 + 8 = 12
Rest of the options is incorrect because of the correctness of option (a).
(a) 281 (b) 301
(c) 291 (d) 241
(e) None of these
Answer (d) is correct.
(a) 1575 (b) 1665
(c) 1185 (d) 1395
(e) None of these
Answer (a) is correct.
Explanation: Number of racks =15
Number of books on each rack = 105
Therefore, total number of books \[=\text{ }105\times 15=1575\]
![]()
So, there are 1575 books in the school library.
Rest of the options is incorrect because of the correctness of option (a).
You need to login to perform this action.
You will be redirected in
3 sec
