Problem-Solving
Category : 4th Class
Problem - Solving
OBJECTIVES
· Students will be develop the ability to understand what the goal of the problem is and what rules could be applied that represent the key to solving the problem.
· They will develop abstract thinking and creative approach.
INTRODUCTION
The process of working through details of a problem to reach a solution. Problem solving may include mathematical or systematic operations and can be a gauge of an individual's critical thinking skills.
Four Stages of Problem Solving
Stage 1: Understand and explore the problem;
Stage 2: Find a strategy;
Stage 3: Use the strategy to solve the problem;
Stage 4: Look back and reflect on the solution.

Example 1:
Jay is 85 cm tall. His father is twice as tall as Jay. How tall is Jay's mother if she is 15 cm shorter than his father?
(a) 1 m 55 cm (b) 1 m 66 cm
(c) 1 m 72 cm (d) 1 m 90 cm
Ans. (a)
Explanation:
Jay's height = 85 cm
His father's height \[=85\times 2=170\]cm
His mother's height = 170 - 15 = 155 cm
= 1 m 55 cm.
Example 2:
There are 18 pupils in a group. There are 10 boys and the rest are girls 7 pupils are wearing glasses. If 3 girls are wearing glasses, how many boys are not wearing glasses?
(a) 3 (b) 6
(c) 8 (d) 9
Ans. (b)
Explanation:
Total pupils = 18
Number of boys = 10
Number of girls = 18 - 10 = 8
Number of pupils wearing glasses = 7
Number of girls wearing glasses = 3
Number of boys wearing glasses = 7 - 3 = 4
Number of boys not wearing glasses = 10 - 4 = 6.
Example 3:
If ![]() ,
, ![]() and
and ![]() , then which of the following is definitely wrong?
, then which of the following is definitely wrong?
(a) ![]() (b)
(b) ![]()
(c) ![]() (d)
(d) ![]()
Ans. (d)
Explanation:
![]()
Options (a), (b) and (c) are correct but option (d) is definitely wrong as ![]()
Example 4:
Tom is\[6\frac{3}{4}\] years old. John is \[6\frac{1}{2}\] years old. Jim is 6.25 years old. Mark is 6.5 years old. Which two children are at the same age?
(a) Tom and Mark (b) John and Jim
(c) Tom and Jim (d) John and Mark
Ans. (d)
Explanation:
1 year = 12 months
\[\frac{3}{4}\] year = 9 months
Hence, Tom's age = 6 years 9 months
\[\frac{1}{2}\] year = 6 months.
Hence, John's age = 6 years 6 months
Jim's age = 6 years 3 months
Mark's age = 6 years 6 months.
Therefore, John and Mark are at the same age.
Direction (Examples. 5 - 8): Read the information given below carefully and answer the following questions. A, B, C, D, E, F and G are sitting in a row facing north.
· A is sitting at the right end and G is sitting at the left end.
· F is the immediate right of E.
· E is 4th to the right of G.
· C is the neighbour of B and D.
· D is third to the left of A.
Example 5:
Who is/are to the left of C?
(a) Only B (b) G, B and D
(c) G and B (d) D, E, F and A
Ans. (c)
Explanation:
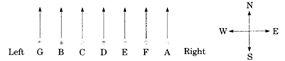
G and B are to the left of C.
Example 6:
Which of the following statements is not true?
(a) A is at one of the ends.
(b) E is to the immediate right of D.
(c) G is at one of the ends.
(d) F is sitting between E and A.
Ans. (b)
Explanation:
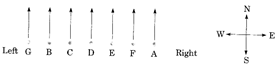
E is to the immediate right of D.
Example 7:
Who are the neighbours of B?
(a) C and D (b) G and F
(c) C and G (d) C and E
Ans. (c)
Explanation:
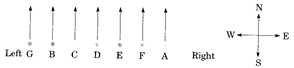
C and G are the neighbours of B.
Example 8:
What is the position of D?
(a) Between B and C
(b) Extreme left
(c) Centre
(d) Extreme right
Ans. (c)
Explanation:
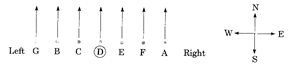
D is in Centre.
You need to login to perform this action.
You will be redirected in
3 sec
