Bodmas Application
Category : 5th Class
LEARNING OBJECTIVES
This lesson will help you to-
Real – Life Example
Amazing Fact
QUICK CONCEPT REVIEW
Lesson in a Nutshell
BODMAS: BODMAS is the sequence for working out and constructing mathematical equations and formulas containing more than one calculation. This methodology is commonly referred to as the order of mathematical operations.
Operations: "Operations" in mathematics refer to addition, subtraction, multiplication, division, etc. If it isn't a number it is probably an operation.
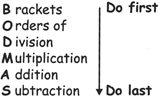
B RACKETS ( ) [ ] { }
O RDER POWER OF \[\sqrt{{}}{{\left( {} \right)}^{2}}\]
D IVIDE \[/\div \]
M ULTIPLY \[*\times \]
A DDITTION +
S UBTRACTION ____
Steps to simplify the order of operation using BODMAS rule:
For Example : \[\left( 6+4 \right)\times 5\]
First solve inside ‘brackets’ 6 + 4 = 10, then \[10\times 5=50.\]
For Example : 3 of 4 +n 9
First solve ‘of’ \[3\times 4=12,\] then 12 + 9 = 21.
We know that, when division and multiplication follow one another, then their order in that part of the equation is solved from left side to right side.
For Example: \[15\div 3\times 1\div 5\]
‘Multiplication’ and ‘Division’ perform equally, so calculate from left to right side. First solve \[15\div 3=5,\] then \[5\times 1=5,\] then \[5\div 5=1.\]
We know that, when addition and subtraction follow one another, then their order in that part of the equation is solved from left side to right side.
For Example: 7 + 19 – 11 + 13
‘Addition and ‘Subtraction’ perform equally, so calculate from left to right side. First solve 7 + 19 = 26, then 26 – 11 = 15 and then 15 + 13 = 28.
Historical preview
Misconcept/ Concept
Misconcept: Some question, for example are written as \[6\div 2\left( 1+2 \right).\] There is no sign between 2 and (. This is often misinterpreted as division.
Concept: The absence of sign indicates a multiplication So, this expression is actually \[-6\div {{2}^{*}}\left( 1+2 \right).\] The BODMAS rule says –
First Brackets
Then Of
Then Division and Multiplication in the order they appear from left to right.
Then Addition and Subtraction in the order they appear from left to right.
Thus note that BODMAS rule does not say that division comes before multiplication. It also does not say that Addition comes before subtraction.
In the above example, first we will solve the brackets: 1 + 2 = 3. So now the equation gets converted to \[6\div {{2}^{*}}3.\] Now the division AND multiplication will be evaluated from left to right. So \[6\div 2=3\] and \[{{3}^{*}}3=9.\] The correct answer is 9.

These are simple rules need to be followed for simplifying or calculating using BODMAS rule.
Rules of BODMAN are same with integers, decimals and fractions.

You need to login to perform this action.
You will be redirected in
3 sec
