5th Class Mathematics Operation on Fractions Operation on Fractions

 Operation on Fractions

Operation on the Fractions

In the previous chapter, we have studied about the fractions. In this chapter we will study operations on the fractions, like addition, subtraction, multiplication and division on fractions.

Addition of Fractions

Make the denominator of fractions same by multiplying a suitable number of the numerator and denominator of both fractions. The common denominator is the denominator of the resultant fraction and addition of numerators is the numerator of the resultant fraction.

•        Example

Add \[\frac{12}{16}\] and \[\frac{13}{16}.\]

Solution:

            \[\frac{12}{16}\,+\,\frac{13}{16}\,=\,\frac{12+13}{16}\,=\,\frac{25}{16}\]

•       Example

Add \[\frac{10}{9}\] and \[\frac{9}{10}.\]

Solution:

\[\frac{10}{9}\,=\,\frac{10}{9}\,\times \,\frac{10}{10}\,=\,\frac{100}{90}\]

            \[\frac{9}{10}\,=\,\frac{9}{10}\,\times \,\frac{9}{9}\,=\,\frac{81}{90}\]

Therefore, their sum = \[\frac{10}{90}\,+\,\frac{81}{90}\,=\,\frac{100+81}{90}\,=\,\frac{181}{90}\]

Subtraction of Fractions

Make the denominator of each fraction same by multiplying a suitable number to the numerator and denominator of both fractions. The common denominator is the denominator of resultant fraction and result of numerators after subtraction is the numerator of the resultant fraction.

•        Example

Subtract \[\frac{23}{27}\] from \[\frac{30}{27}.\]

•     Example

Subtract \[\frac{16}{17}\] from \[\frac{18}{19}.\]

Solution:

\[\frac{16}{17}\,=\,\frac{16\times 19}{17\times 19}\,=\,\frac{304}{323}\]

\[\frac{18}{19}\,=\,\frac{18\times 17}{19\times 17}\,=\,\frac{306}{323}\]

Therefore, difference \[=\,\frac{306}{323}\,-\,\frac{304}{323}\,=\,\frac{2}{323}\]

Multiplication of Fractions

Numerator is multiplied to numerator and denominator is multiplied to denominator on multiplication of any two fractions.

•      Example

Find the product of \[\frac{13}{20}\] and \[\frac{16}{19}.\]

Solution:

\[\frac{13}{20}\times \frac{16}{19}\,=\,\frac{13\times 16}{20\times 19}\,=\,\frac{208}{380}\]

•      Example

Find the product of \[\frac{23}{15}\] and \[\frac{175}{207}.\]

Solution:

            \[\frac{23}{25}\times \frac{175}{207}\,=\,\frac{23\times 175}{25\times 207}\,=\,\frac{7}{9}\,\]

\[\{\because \,23\,\times \,9\,=\,207\,and\,25\,\times \,7\,=\,175\}\,\]

Multiplication of a fraction and a Whole number

Simply, numerator of a fraction is multiplied by a whole number and denominator remains same as the denominator of a fraction.

•      Example

Find the product of \[\frac{26}{15}\] and 22.

Solution:

            \[\frac{26}{15}\,\times \,22\,=\,\frac{26\times 22}{15}\,=\,\frac{572}{15}\]

•      Example

Find the product of 25 and \[\frac{127}{140}.\]

Solution:

\[25\times \,\frac{127}{140}\,=\,\frac{25\times 127}{140}\,=\,\frac{635}{28}\]

Division of Fractions

For division of fractions, we use following steps:

Step 1: Reverse the order of divisor fraction so that denominator becomes numerator and numerator becomes denominator and put the sign of multiplication in place of division.

Step 2: Multiply numerator by numerator and denominator by denominator.

•      Example

Divide \[\frac{15}{28}\] by \[\frac{15}{28}\]

Solution:

\[\frac{15}{28}\,\div \,\frac{7}{3}\,=\,\frac{15}{28}\,\times \,\frac{3}{7}\,=\,\frac{45}{196}\]

•      Example

Divide \[\frac{20}{33}\] by \[\frac{5}{11}.\]

Solution:

\[\frac{20}{33}\,\div \,\frac{5}{11}\,=\,\frac{20}{33}\,\times \,\frac{4}{3}\]

Division of a Fraction by a Whole Number and Vice Versa

The steps used for division are:

Step 1: Whole number is written as a fraction by taking 1 as denominator.

Step 2: Reverse the order of divisor so that denominator becomes numerator and numerator becomes denominator, and put sign of multiplication in place of division.

Step 3: Multiply numerator with numerator and denominator with denominator.

•      Example

Divide \[\frac{12}{15}\] by 25.

            Solution:

            \[\frac{12}{15}\,\div \,25\,=\,\frac{12}{15}\,\times \,\frac{1}{25}\,=\,\frac{12}{15\times 25}\,=\,\frac{4}{125}\]

•      Example

Divide 216 by \[\frac{27}{36}.\]

Solution:

\[216\,\div \,\frac{27}{36}\,=\,\frac{216}{1}\,\times \,\frac{36}{27}\]

\[=\,\frac{216\,\times \,36}{27}\,=\,24\,\times \,12\,=\,288\]

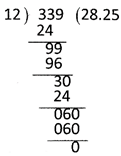
Conversion of a Fraction into Decimals

Divide the numerator by denominator till the remainder becomes zero. If the digits in the numerator goes off, than take other digits as 0 and put the decimal point in the quotient.

•       Example

Convert \[\frac{339}{12}\] into decimals.

Solution: