Comparing Quantities
- Ratio is a method of comparing two quantities of the same kind by division.
- The symbol used to write a ratio is'.-'and is read as \[';'\]is to'.
- A ratio can be expressed as a fraction.
- A ratio is always expressed in its simplest form.
- A ratio does not have any unit, it is only a numerical value.
- A ratio consists of two terms. The first term is called the antecedent and second term is called the consequent.
- A ratio can be written in its simplest form by dividing the antecedent and the consequent by their H.C.F.
- The antecedent and the consequent of a ratio cannot be interchanged.
- To express two terms in a ratio, they should be in the same units of measurement.
- When two ratios are equal they are said to be in proportion, the symbol for proportion is \[::\] and is read as 'as to'.
- The two terms in the middle of a proportion are called means and the first and the last terms are called extremes.
- If two ratios are to be equal or to be in proportion, their product of means should be equal to the product of extremes.
- lf a:b :: c:d then the statement ad = be holds good.
- lf a:b and b: c are in proportion such that \[{{\operatorname{b}}^{2}}=ac\]hen b is called the mean proportional of a:b and b:c.
- Multiplying or dividing the terms of the ratio by the same number gives equivalent ratios.
- Unitary method:
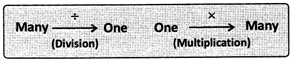
- To find the value of many quantities when the value of one is given, the operation is multiplication (x).To find out value of one when the value of many is given. The operation is division (-).To find out value of many when the value of many is given, unitary method can be used.
- Another way of comparing quantities is percentage. The word percent means per hundred. Thus 12% means 12 parts out of 100 parts.
- Fractions can be converted into percentages and vice-versa.
e.g., (i)\[\frac{2}{5}=\frac{2}{5}\times 100%=40%\]
(ii)\[25%=\frac{25}{100}=\frac{1}{4}\]
- Decimals can be converted into percentages and vice-versa.
- g. (i) \[0.36=0.36\times 100%=36%\]
(ii)\[43%=\frac{43}{100}=0.43\]
- If a number is increased by a% and then decreased by a% or is decreased by a% and then increased by a%, then the original number decreases by \[\frac{{{a}^{2}}}{100}\]%.
- A number can be split into two parts such that one part is P% of the other. Then the two parts are
\[\frac{100}{100+2}\times \,number\,and\,\frac{p}{100+P}\times number\]
- If the circumference of a circle is increased (or) decreased by P% then the radius of a circle in- increases (or) decreases by P%,
- Gain = Selling Price (S.P.) - Cost Price (C.P.)
- Loss=C.P.-S.P.
- Gain%\[=\frac{gain}{C.P.}\times 100%\]
- Loss%\[=\frac{loss}{C.P.}\times 100%\]
- \[\operatorname{S}.P.=\left( \frac{100+gain%}{100} \right)\times C.P.=\left( \frac{100-loss%}{100} \right)\times C.P.\]
- \[\operatorname{C}.P=\left( \frac{100}{100+gain%} \right)\times S.P.=\left( \frac{100}{100-loss%} \right)\times S.P.\]
- \[\operatorname{S}.I.=\frac{PTR}{100}\]
- I. = Simple Interest
- P = Principal
- T=Time
- R = Rate percent per annum
- Amount (A) = Principal + Interest
\[=p+\frac{PTR}{100}p\left( 1+\frac{TR}{100} \right)\]
- \[\operatorname{R}\times T=100\left( N-1 \right)\]
Where R = rate percent
T = time
N = The number of times the sum gets multiplied (i.e., doubled, tripled ....etc.)
- I. is calculated uniformly on the original principal throughout the time period.

