Geometry
Category : 7th Class
Geometry
In our daily life we observe different geometrical shapes. These geometrical shapes are not only the matter of study of mathematics but are directly related without daily life. The basic geometrical figures are made up of lines and angles.
Line Segment
It is the straight path between two points. In other words we can say that it has two end points and is of finite length.
Ray
When a line segment extends infinitely in one direction, it is called a ray. Simply we can say that a ray has one end point and infinite length.
Line
When both end of a line segment extended infinitely, it is known as a line. Simply we can say that a line has no end point and infinite length.
Parallel Lines
Two lines are said to be parallel if the distance between them always remains same at each and every point. The parallel lines never intersect each other.
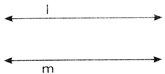
In other words we can say that if two lines do not have any common point that they are said to be parallel. In the figure I and parallel lines.
Angle
If two rays have common end point then the inclination between two rays is called an angle.
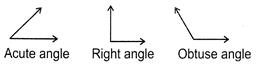
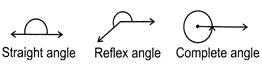
Types of Angles
The following are different types of angles:
Triangles
The word triangle is derived from Greek word, tri means three and hence, it refers to a shape consisting of three internal angles. Obviously the shape consists of three sides. Hence, a triangle can be defined as a polygon having three sides.
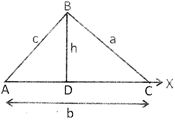
Basic Concepts of Triangles
The general shape of a triangle is shown below:
Properties of a Triangle
Triangle are one of the basic geometrical shape and have different properties based on their sides and angles.
Types of Triangle
Congruent Triangles
Two geometrical figures are said to be congruent if they have same shape and size. For example, two angles are said to be congruent if they have same measures similarly two line segments are said to be congruent if they have same length. So two triangles are said to be congruent if their corresponding sides and angles are equal.
In a right angled triangle AB = 3 units, BC = 4 units then AC is equal to:
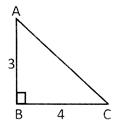
(a) 3 units (b) 4 units
(c) 5 units (d) 6 units
(e) None of these
Ans. (c)
Explanation: \[A{{C}^{2}}=A{{B}^{2}}+\,\,B{{C}^{2}}\,\,\,\Rightarrow A{{C}^{2}}={{3}^{2}}+\,\,{{4}^{2\,\,}}\,\,\,\Rightarrow \,\,AC=\,\,5\,units\]
In the following figure, the missing angle of the triangle is:

(a) \[30{}^\circ \] (b) \[25{}^\circ \]
(c) \[20{}^\circ \] (d) \[60{}^\circ \]
(e) None of these
Ans. (b)
Explanation: Missing angle of the triangle
\[=180{}^\circ -(127{}^\circ +28{}^\circ )=180{}^\circ -155{}^\circ =25\]
Exterior Angle of a Triangle
The angle between the produced side and the adjacent side of the triangle is called exterior angle. The exterior angle is equal to the sum of two opposite interior angles of the triangle. In the figure below \[\angle ABD,\,\,\angle CAF\,\,and\,\,\angle ACE\] are the exterior angles of the triangle.
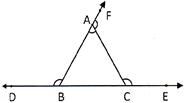
Thus,
\[\angle ACE=\angle BAC+\angle ABC\]
\[\angle ABD=\angle BAC+\angle ACB\]
\[\angle CAF=\angle ABC+\angle ACB\]
You need to login to perform this action.
You will be redirected in
3 sec
