Practical Geometry
Category : 7th Class
Practical Geometry
(i) S.S.S: A triangle can be drawn given the lengths of its three sides.
(ii) S.A.S: A triangle can be drawn given the lengths of any two sides and the measure of the angle between them.
(iii) A.S.A: A triangle can be drawn given the measures of two angles and the length of the side included between them.
(iv) R.H.S: A triangle can be drawn given the length of hypotenuse of a right angled triangle and the length of one of its legs.
(a) an equilateral triangle, if all of its sides are equal.(b) an isosceles triangle, if any two of its sides are equal.
(c) a scalene triangle, if all of its sides are of different lengths.
(a) an acute angled triangle, if each one of its angles measures less than \[{{90}^{o}}\].
(b) a right angled triangle, if any one of its angles measures\[{{90}^{o}}\].
(c) an obtuse angled triangle, if any one of its angles measures more than 90°.
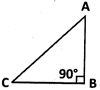
\[\operatorname{Here},A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
