Symmetry
- Linear symmetry: If a line divides a given figure into two coinciding parts, we say that the figure is symmetrical about the line and the line is called the axis of symmetry or line of symmetry.
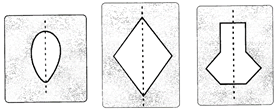
- A line of symmetry is also called a mirror line.
- A figure may have no line of symmetry, only one line of symmetry, two lines of symmetry or multiple lines of symmetry.
- Regular polygons have equal sides and equal angles. They have multiple lines of symmetry.
- Each regular polygon has as many lines of symmetry as its sides.
- A scalene triangle has no line of symmetry.
- A parallelogram has no line of symmetry.
- A line segment is symmetrical about its perpendicular bisector.
- An angle with equal arms has one line of \[\leftrightarrow \]symmetry.
- An isosceles triangle has one line of symmetry.
- An isosceles trapezium has one line of symmetry.
- A semicircle has one line of symmetry.
- A kite has one line of symmetry.
- A rectangle has two lines of symmetry.
- A rhombus has two lines of symmetry.
- An equilateral triangle has three lines of symmetry
- A square has four lines of symmetry.
- A circle has an infinite number of lines of symmetry.
- In English alphabet, the letters A, B, C, D, E, K, M, T, U, V, W and Y have one line of symmetry and the letters H, I, X have two lines of symmetry
- In English alphabet, the letters F, GJ, L, N, P, Q, R, S and Z have no line of symmetry The letter 0 has many lines of symmetry.
- The line symmetry is closely related to mirror reflection. When dealing with mirror reflection, we have to take into account the left\[\leftrightarrow \] right changes in orientation.
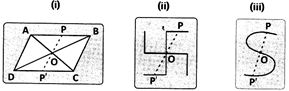
- Point symmetry: A figure is said to be symmetric about a point 0, called the centre of symmetry, if corresponding to each point P on the figure, there exists a point P' on the other side of the centre, which is exactly opposite to the point P and lies on the figure.
Note: A figure that possesses a possesses a point symmetry, regains its original shape even after beging rotated through \[\mathbf{18}{{\mathbf{0}}^{\mathbf{o}}}\]
|
Letters of the English alphabet
|
Line of symmetry
|
|
A,M,T,U,V,W and Y
|
Vertical
|
|
B,C,D,E and K
|
Horizontal
|
|
H,I and X
|
Both vertical and horizontal
|
|
F,G,J,L,N,P,Q,R,S and Z
|
None
|
|
O
|
Infinitely many
|
- Rotational symmetry: A figure is said to have rotational symmetry if it fits onto itself more than once during a complete rotation.
- The number of times a figure fits onto itself in one complete rotation is called the order of
- Rotational symmetry.
- A line segment AB possesses a rotational symmetry of order 2 about the midpoint 0 of the line segment.
- An equilateral triangle ABC possesses a rotational symmetry of order 3 about the point of intersection 0 of the bisectors of the interior angles.
- A square ABCD possesses a rotational symmetry of order 4 about the point of intersection 0 of its diagonals.
- A rhombus ABCD possesses a rotational symmetry of order 2 about the point of intersection 0 of its diagonals.
- A rectangle ABCD possesses a rotational symmetry of order 2 about the point of intersection 0 of its diagonals.
- A parallelogram ABCD possesses a rotational symmetry of order 2 about the point of intersection 0 of its diagonals.
- A regular pentagon possesses a rotational symmetry of order 5 about the point of intersection 0 of the perpendicular bisectors of the sides of the pentagon.
- A regular hexagon possesses a rotational symmetry of order 6 about the centre 0 of the hexagon.
- A circle with centre 0 possesses a rotational symmetry of an infinite order about the centre 0.
- The following letters of the English alphabet have rotational symmetry about the point marked on them.


