Inserting Missing Number
Category : 8th Class
Inserting Missing Number
Learning Objectives
Inserting the Missing Numbers
In such type of questions, a figure, a set of figures or a matrix is given, each of which bears certain characters, and be it numbers, letters or a group of letters / numbers following a certain pattern. The candidate is required to decipher this pattern and accordingly find the missing character in the figure.
Example 1
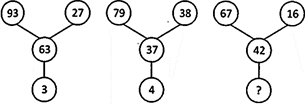
(a) 5 (b) 6
(c) 8 (d) 9
(e) None of these
Answer: (d)
Explanation: The sum of numbers on right and centre subtracted from the number on the left gives the number at the bottom, i.e.
\[93-\left( 27+63 \right)=3;\text{ }79-\left( 38+37 \right)=4,\]
Similarly, \[67-\left( 16+42 \right)=9\]
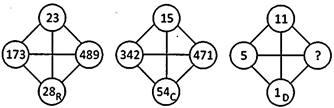
(a) 3 (b) 8
(c) 10 (d) 14
(e) None of these
Answer: (c)
Explanation: Letter R is 18th in order of alphabetical series. So the product of vertically opposite numbers + 18 (R) = the sum of two horizontally opposite number, i.e.,
\[(28\times ~23)+18=173+489\]
\[644+18=662\]
\[662=662\]
Letter C is 3rd in order, so
\[(54~\times 15)+3=342+471\]
\[810+3=813\]
\[813=813\]
Similarly, letter D is 4th in order
\[(1\times ~11)+4=5+?\]
\[11+4=5+?\]
\[15=5+?\] or \[5+?=15\]
So' \[?=15-5=10\]
Commonly Asked Question
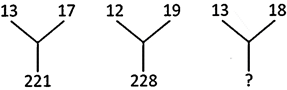
(a) 31 (b) 229
(c) 234 (d) 312
(e) None of these
Answer: (c)
Explanation: The number at the bottom is the product of two numbers at the top, i.e.,
\[13~\times 17=221\]
\[12\times ~19=228,\]
Similarly, \[13~\times 18=234\]

(a) 693 (b) 939
(c) 981 (d) 993
(e) None of these
Answer: (c)
Explanation: The squares of two numbers on the top placed side by side gives the number inside the bottom triangle, i.e.,
\[{{6}^{2}}\] and \[{{3}^{2}}=369\]
\[{{2}^{2}}\] and \[{{5}^{2}}=425,\]
Similarly, \[{{3}^{2}}\] and \[{{9}^{2}}=981.\]
You need to login to perform this action.
You will be redirected in
3 sec
