Linear Equation in Two Variables
Category : 9th Class
Previously we have studied about a linear polynomial in two variable. The general form of linear polynomial in two variable is \[ax+by+c\], where a, \[b\ne 0\]. In this chapter we will study about linear equation in two variable.
Suppose \[p(x)=ax+by+c\] is a linear polynomial in two variable where a, \[b\ne 0\]. Then \[p(x)=0\] is a linear equation in two variable i.e. \[ax+by+c=0\], where a, \[b\ne 0\] is a linear equation in two variable.
![]() Solution of a Linear Equation
Solution of a Linear Equation
\[x=p\]and\[y=q\] is called the solution of a linear equation \[ax+by+c=0\] if \[ap+bq+c=0\]
![]()
Which one of the following equations is not a linear equation in two variable?
(a) \[4x+\frac{7}{2}y=4\]
(b) \[\frac{4}{x}+\frac{7}{y}=4\]
(c) \[\frac{x+3}{x-3}=4\]
(d) \[3x+7y+87=0\]
(e) None of these
Answer: (b)
Explanation:
In \[\frac{4}{x}+\frac{7}{y}=4\]
The power of variable x and y is -1. Therefore, it is not a linear equation.
![]() Graph a Linear Equation in Two Variable
Graph a Linear Equation in Two Variable
The general form of linear equation in two variable is \[ax+by+c=0\]
\[\Rightarrow \]\[by=ax-c\] \[\Rightarrow \]\[y=\left( \frac{-a}{b} \right)x-\frac{c}{a}\]
It is the form
\[y=mx+c\] Represents a line where \[m=\left( \frac{-a}{b} \right)\] and \[c=\frac{c}{a}\] and m is known as the slope of this line. That is why, we can say that the graph of a linear equation represented by a line.
![]()
The slope of line \[4x+\text{3y}-\text{4}=0\] is______
(a) \[\frac{3}{4}\]
(b) \[\frac{-4}{3}\]
(c) \[\frac{4}{3}\]
(d) \[\frac{-3}{4}\]
(e) None of these
Answer: (b)
Explanation:
\[4x+3y-4=0\]
\[\Rightarrow \]\[3y=-4x+4\] \[\Rightarrow \]\[y=\left( \frac{-4}{3} \right)x+4\]
Here, \[m=\frac{-4}{3}\]
Graph of \[\mathbf{ax+by+c=0}\]
The following steps are followed to draw a graph:
Step 1: Express \[x\] in terms of y or y in terms of \[x\].
Step 2: Select at least three values of y or \[x\] and find the corresponding values of\[x\] or y respectively, which satisfies the given equation, write these values of \[x\] and y in the form of table.
| \[x\] | |||
| \[y\] |
Step 3: Plot ordered pair (\[x\], y) from the table on a graph paper.
Step 4: Join these points by a straight line. Note: Every point on the line is a solution of linear equation in two variable i.e. there are infinite number of solution of a linear equation.
![]()
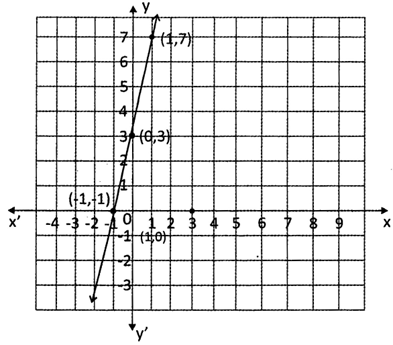
Draw the graph of \[4x-y+3=0\].
Solution:
Step 1: Here it is easy to write y in terms of\[x\] \[\Rightarrow \] \[y=4x+3\].
Step 2: \[y=4x+3\]
if \[x=0\] \[\Rightarrow \] \[y=3\]
\[\Rightarrow \]\[x=-1\] \[\Rightarrow \] \[y=-1\]
| \[x\] | 0 | 1 | -1 |
| \[y\] | 3 | 7 | -1 |
Step 3 and Step 4:
You need to login to perform this action.
You will be redirected in
3 sec
