Gravitation
Category : 9th Class
Gravitation
Chapter Overview
According to Newton's first law of motion, planets and satellites can move in circular orbits only if some force is acting on them. Sir Issac Newton proposed that all particles or objects in the Universe attract each other in the same manner as the earth attracted the apple.
"The force of attraction between any two particles in the Universe is called Gravitation or gravitational force. Newton showed that gravitational force between two masses varies inversely proportional to the square of the distance between them. This fact was proved by him on the basis of Kepler's laws of planetary motion.
The German astronomer Johannes Kepler worked out on three empirical laws that govern the motion of the planets around the Sun.
(1) Kepler's First Law:
(i) Law of Orbits: Every planet revolves around the sun in an elliptical orbit with the Sun situated at one of the foci of the ellipse.

Fig. 2.1.
P = Position of the planet
\[{{P}_{1}}\] = Position of the Sun.
(2) Kepler's Second Law:
(ii) Law of Areas: Each planet moves in such a way that an imaginary line drawn from the sun to the planet sweeps out equal area in equal interval of time.
According to Kepler's second law of motion if,
Time taken by the planet to move from \[{{P}_{1}}\]to\[{{P}_{2}}=Tim\]taken by the planet to move from\[{{P}_{3}}\]to\[{{P}_{4}}\]then
Area\[{{P}_{1}}S{{P}_{2}}=\]Area\[{{P}_{3}}S{{P}_{4}}\]
because the distance of the planet at position \[{{P}_{1}}\]is mor than the distance of the planet at position \[{{P}_{3}}\]from the sun, so \[{{P}_{1}}S>{{P}_{3}}S\]
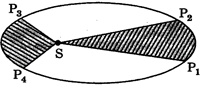
Fig .2.2.
\[\text{Speed=}\frac{\text{Distance}}{\text{Time}}\]or\[\text{Time}\frac{\text{Distance}}{\text{Speed}}\]
So, for equal time intervals speed along \[{{P}_{1}}{{P}_{2}}<\]Speed along \[{{P}_{3}}{{P}_{4}}\]
Conclusion: Velocity of a planet when closer to the sun is more than its velocity when away from the sun.
Law of Periods: According to Kepler's third law of planetary motion the cube of the planet's average-distance from the sun is directly proportional to the square of the time period of revolution of the planet around the sun.
\[{{T}^{2}}\propto {{r}^{3}}\]or\[{{T}^{2}}=\](constant)\[{{r}^{3}}\]\[\frac{{{T}^{2}}}{{{r}^{3}}}=\]constant
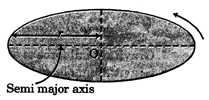
Fig. 2.3.
Newton suppose that a planet (earth) revolves around the earth in a circular path of radius r. Let v be orbital velocity of the earth.
When an object moves in a circular path of radius r with a velocity v, it experiences an acceleration \[=\frac{{{v}^{2}}}{r}\](centripetal acceleration)
So, centripetal force is given by\[F=\frac{m{{v}^{2}}}{r}\]
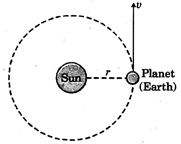
Fig. 2.4.
Let T = time taken by the earth to complete one revolution around the sun, then
\[v=\frac{Dis\tan ce}{time}=\frac{2\pi r}{T}\]
Put the value of v from above relation in eq. (1)
\[F=\frac{m}{r}{{\left( \frac{2\pi r}{T} \right)}^{2}}\]
\[F=\frac{4{{\pi }^{2}}mr}{{{T}^{2}}}\] …(2)
but from Keplerfe third law\[{{T}^{2}}=k{{r}^{3}},\] where k is constant
\[\therefore \]equation (2) becomes \[F=\frac{4{{\pi }^{2}}m}{k{{r}^{2}}}\]
or \[F=\frac{1}{{{r}^{2}}}\] …(3)\[\left( \because \frac{4{{\pi }^{2}}m}{k}=cons\tan t \right)\]
"Thus, the gravitational force between the sun and the planet (say earth) is inversely proportional to the square of the distance between them.
This statement or hypothesis is valid for all particles or bodies in the universe.
According to this law, the force of attraction between two particles or bodies is:
(i) Directly proportional to the product of their masses.
(ii) Inversely proportional to the square of the distance between these particles or bodies.
3. The gravitational forces between two bodies form an action-reaction pair.
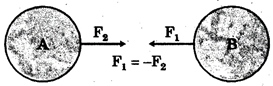
Fig. 10.5
Gravity: The gravitational force between a body and the earth is called gravity.
The acceleration with which a body falls to words the earth due to earth’s gravitational pull is known as acceleration due to gravity. It is represented by g. Hence, all bodies of irrespective of their masses fall down with constant acceleration.
Definition of free fall: The falling body on which only force of gravitation of the earth acts is known as freely falling body and such fall of a body is known as free fall.
A freely falling body acceleration is equal to acceleration due to gravity (g).
SI unit of g is the same as that of acceleration i.e. \[m/{{s}^{2}}\].
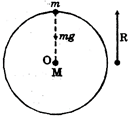
Fig.7.1.
Let F be the force of attraction between the body and the earth. According to Newton’s Universal Law of Gravitation
\[F=\frac{GMm}{{{R}^{2}}}\] ...(1)
This force exerted by the earth produces an acceleration in the body due to which the body moves downward according to Newton’s second law of motion.
force = mass x acceleration
\[F=m\times a\]
replace a by g because acceleration produced by the earth represented by ‘g’.
so F = mg ...(2)
From (1) and (2) \[mg=G\frac{Mm}{{{R}^{2}}}\]
\[g=\frac{GM}{{{R}^{2}}}\]
Remember: Value of g is independent of the mass, shape and size of the body but depends upon the mass and radius of the earth.
Calculation of the acceleration due to gravity (g)
\[\because \] \[g=\frac{GM}{{{R}^{2}}}\]
Where G = Gravitational constant \[=6.673\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\]
M =mass of earth\[=6\times {{10}^{24}}kg\]
R = Radius of earth \[=6.4\times {{10}^{6}}m\]
Putting all values in above relation
\[g=\frac{6.673\times {{10}^{-11}}N{{m}^{2}}k{{g}^{-2}}\times 6\times {{10}^{24}}kg}{{{(6.4\times {{10}^{6}}m)}^{2}}}\]\[g=9.8m/{{s}^{2}}\].
However, in solving numerical problems for the sake of convenience i.e. to make the calculation easy, the value g is taken as a round figure of \[10\text{ }m/{{s}^{2}}\]
(1) Variation in the value ofg with the shape of the earth
The earth is not spherical in shape but it is egg shaped,so, the radius of earth (R) is not constant throughout.
Hence, the value of g is different at different points on the earth.
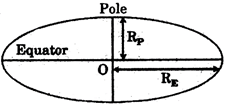
Fig. 9.1.
\[{{g}_{E}}=\frac{GM}{R_{E}^{2}}\] ..(2)
Value of ’g’ at poles is given by
\[{{g}_{p}}=\frac{GM}{R_{p}^{2}}\]
Dividing eq. (3) by eq. (2)
\[\frac{{{g}_{p}}}{{{g}_{E}}}={{\left( \frac{{{R}_{E}}}{R_{p}^{{}}} \right)}^{2}}\]
Since \[{{R}_{E}}>{{R}_{p}}\]
\[\therefore \] \[{{g}_{p}}>{{g}_{E}}\]
(2) Effect of altitude \[g=\frac{1}{{{R}^{2}}}\]
The value of g is inversely proportional to the square of the distance from the centre of the earth as we go up the surface of the earth, the distance from the centre of the earth increases and hence the value of g decreases i.e. the value of g decreases with height (altitude).
Due to this reason that the value of g is less at mountains than on plains.
(3) Effect of depth: As we go below the surface of the earth the acceleration due to gravity goes on decreasing and becomes zero at the centre of the earth,
So, the value of g is maximum at the earth b surface arid decreases with depth and becomes zero at the centre of the earth.
Remember: At the centre of the earth depth d=R
Value of g at the centre of earth is zero.
|
Parameter |
G |
G |
|
1. Definition |
It is equal to force of attraction acting between two bodies each of unit mass whose centres are placed unit distance apart.
Fig. 10.1 |
It is the uniform acceleration produced in a body when it falls freely under the effect of gravity alone.
Fig. 10.2 |
|
2. S.I. unit |
It is n ever zero. It is scalar quantity. |
It is zero at the centre of the earth. It is a vector quantity. |
All the equations of motion for the uniformly accelerated bodies moving in a straight line are applicable to the freely falling bodies.
All freely falling bodies fall with a uniform acceleration due to gravity so acceleration (a) produced in a body moving in a straight line = acceleration due to gravity (g)
Distance (s) travelled by a body along a straight line
= Height above the surfaces of the earth (A).
General equations of motion Equations of motion for freely falling bodies
1.\[v=u+at\] \[v=u+gt\]
2.\[s=ut+\frac{1}{2}a{{t}^{2}}\] \[h=ut+\frac{1}{2}g{{t}^{2}}\]
3. \[{{v}^{2}}={{u}^{2}}+2as\] \[{{v}^{2}}={{u}^{2}}+2gh\]
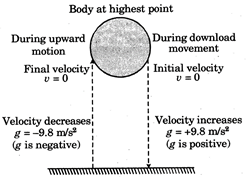
Fig.11.1
Sign convention:
When a body is dropped from a certain height its initial velocity u is taken as zero.
Important Logical Concept
If a body is thrown vertically upwards, then the time of ascent is equal to the time of descent. Prove this problem.
Step 1. Let the body attains maximum height in time\[{{t}_{1}}\]at the highest point, the body comes to rest.
So, final velocity of the body is zero i.e., v = 0
\[\because \] \[v=u+g{{t}_{1}}\]
\[0=u-g{{t}_{1}}\] (\[\because \]g is taken as negative)
\[{{t}_{1}}=\frac{u}{g}\]
Step 2. After attaining maximum height, initial velocity u = 0
Let it takes time \[{{t}_{2}}\] to reach the ground and hits the ground with velocity v.
\[v=u+gt\]
\[-v=0-g{{t}_{2}}\]
\[{{t}_{2}}=\frac{v}{g}\] …(2)
Since v = u, because the body hits the ground with the same velocity with which it is thrown vertically upwards, so
\[{{t}_{2}}=\frac{u}{g}\] ...(3)
From equation (1) and (3) time \[{{t}_{1}}=\]time \[{{t}_{2}}\]
Time of ascent == Time of descent.
Mass: Mass of a body is defined as the quantity of matter contained in the body. Because mass of a body is a measure of inertia of the body, so mass is also known as inertial mass.
Unit of mass: S.I. unit of mass is kilogram (kg)
Characteristics of Mass of a body:
Remember: Mass is a scalar quantity.
Weight: The force with which a body is attracted by the earth is known as the weight of the body.
The force with which a body of mass m is attracted by the earth is given by
\[F=ma=m\times g=mg.\]
This force is known as weight of the body. It is denoted by W.
W = mg.
It is a vector quantity.
S.I. unit of weight is same as that of force i.e. newton (N).
Characteristics of Weight:
|
Physical quantity |
Earth |
Moon |
Comparison b/w earth and moon |
|
Mass (kg) |
|
|
The mass of the earth is about 100 times more than that of the moon |
|
Radius (m) |
|
|
The radius of the earth is about is times more than that of moon. Re = 4 Rm |
Prove that weight of an object on the moon is 176th of its weight on the earth.
The weight of the body on the earth will be
\[{{W}_{e}}=\frac{G{{M}_{e}}m}{R_{e}^{2}}\] ...(1)
Similarly, the weight of the body on the moon will be
\[{{W}_{m}}=\frac{G{{M}_{m}}m}{R_{m}^{2}}\] …(2)
Dividing eq. (2) by eq. (1)
\[\frac{{{W}_{m}}}{{{W}_{e}}}=\frac{\frac{G{{M}_{m}}m}{R_{m}^{2}}}{\frac{G{{M}_{e}}m}{R_{e}^{2}}}=\left( \frac{{{M}_{m}}}{{{M}_{e}}} \right)\left( \frac{{{R}_{e}}}{R} \right)_{m}^{2}\] …(3)
\[{{M}_{e}}=100{{M}_{m}}\]
\[{{R}_{e}}=4{{R}_{m}}\]
Substituting the above value in eq. (3)
\[\frac{{{W}_{m}}}{{{W}_{e}}}=\left( \frac{{{M}_{m}}}{100{{M}_{e}}} \right)\times {{\left( \frac{4{{R}_{m}}}{{{R}_{n}}} \right)}^{2}}\]
\[\frac{{{W}_{m}}}{{{W}_{e}}}=\frac{1}{100}\times \frac{16}{1}=\frac{16}{100}\]
\[\frac{{{W}_{m}}}{{{W}_{e}}}\approx \frac{1}{6}\]
\[{{W}_{m}}\approx \left( \frac{1}{6} \right){{W}_{e}}\]
Thrust: Thrust is the total force acting perpendicular on a surface.
Let us consider forces acting on a body in a particular directions in the following examples:
(1) We want to fix a poster on a Notice Board with the help of drawing pins. When we press a drawing pin, we apply a force on the surface area of its head. This force is directed perpendicular to the surface area of the board.
Fig. 13.1
(2) We want to inflate the tube of a bicycle with the help of a bicycle pump. We pull out and then push in the handle of the bicycle pump. We apply a force on the surface area of its piston.
This force is directed perpendicular to the surface area of the piston.
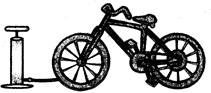
Fig. 13.2.
S.I. unit of thrust: Since thrust is a force, its S.I. unit is same as that of force i.e., (Newton) N.
It is a vector quantity.
Pressure: Pressure is defined as the force acting perpendicular on unit area of the surface.
OR
The thrust per unit area is called pressure. Let us see, on what factors the pressure depends?
Take a pin having a pointed end and a nail having blunt end. Press them against a cardboard by applying the same force. We find that the pin penetrates deep into the cardboard than the nail. In this case, force acting on two points of the cardboard is same. But the area under the tip of the pin is less than under the tip of the nail.
The effect of the forces of the same magnitude on different area is different.
Conclusion: (1) Pressure acting on the surface is inversely proportional to the area of the surface on which force acts.
\[P=\frac{1}{area}\] ...(1)
(2) Take two blocks having same area but one is made of rubber block and other is made of steel. The weight (F = mg) or thrust of rubber block is less than the weight or thrust of the steel block.
Place these blocks on a heap of straw. We find that the straw under the steel block depressed more than the straw under the rubber block.
The pressure is more if force or thrust acting on a given area is large.
Pressure (P) = Force (F) ...(2)
From (1) and (2), Pressure (P) \[=\frac{Force}{area}=\frac{Thrust}{area}\]
\[P=\frac{F}{A}\]
Remember Thrust = Pressure\[\times \]Area
S.I. unit of pressure: \[P=\frac{F}{A}\]
Unit of Pressure (P)\[=\frac{Unit\,of\,force\,(F)}{Unit\,of\,Area\,(A)}=\frac{N}{{{m}^{2}}}=N{{m}^{-2}}\].
1\[N{{m}^{-}}^{2}\] is also known as 1 Pascal (Pa)
\[1N{{m}^{-}}^{2}=1Pascal\]
\[1N{{m}^{-}}^{2}=1Pa\]
so unit of pressure is also Pascal (Pa)
Actually Pascal is a very small unit of pressure, so many times a bigger unit of pressure called "kilopascal’ (kPa) is used.
1kPa = 1 kilo Pascal
\[1kPa=1000Pa=1000N{{m}^{-2}}\]
(1) A camel walks easily on the sandy surface than a man in spite of the fact that a camel is much heavier than a man.
This is because the area of camel's feet is large as compared to the area of man's feet. So the pressure exerted by camel on the sand surface is very small as compared to the pressure exerted by man. Hence camel can walk and run easily on the sandy surface.
(2) A sharp knife is more effective in cutting the objects than a blunt knife.
![]()
Fig. 14.1.
A sharp knife cuts objects better because of its very thin edge and the force of our hand falls over a very small area of the object producing a large pressure. Due to this large pressure it cuts the object easily. In the case of a blunt knife it has thicker edge. Due to its thicker edge, the force of our hand falls over a larger area of the object and produces lesser pressure. Due to this lesser pressure it cuts the object with difficulty.
(3) Railway tracks are laid on large sized wooden or iron sleepers.
\[\because \] \[P=\frac{T}{A}\]or Pressure\[=\frac{Thrust}{Area}\]
The weight (thrust) of the train is spread over a large area of the sleepers. So the pressure acting on the ground under the sleepers is reduced. This prevents the sinking of the ground under the weight of the train.
(4) It is painful to hold a heavy bag having strap made of a strong and thin string.
When we hold a heavy bag having strap made of a strong and thin string, then the area under the strap is small. Hence, large pressure is exerted by the strap on our figures. Due to this large pressure, the strap fends to cut the skin and hence pain is caused.
Fluid: Any substance which has no fixed shape and has the ability to flow is called a fluid.
All liquids and gases do not have fixed shape and can flow and hence are regarded as fluids.
Fluids i.e. liquids and gases enclosed in containers exert pressure in all directions.
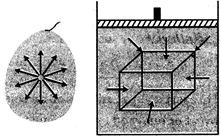
Fig. 15.1.
Pascal's law: According to this law:
"Pressure applied to an enclosed fluid is transmitted undiminished to every portion of the fluid and the walls of the containing vessel."
Mathematical Expression for Pressure Exerted by a Liquid at a point inside it:
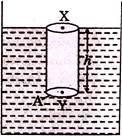
The pressure inside a volume of a liquid depends upon the depth below the surface because deeper we descend, the greater is the weight of the overlying liquid. In order to find the pressure at a point Y, distance h below the free surface of a liquid at rest. Let us imagine a vertical cylinder XY of height h around Y and p is density of liquid.
If A is the cross-sectional area of the cylinder XY.
Volume of the cylinder XY = Area of cross-section\[\times \] height
= Ah
mass of this cylindrical liquid column
= volume of this cylinder \[\times \]density
= \[=Ah\rho \]
and consequently weight of the cylindrical liquid column XY
F = mass of cylindrical liquid column
\[\times \] acceleration due to gravity
\[=Ah\rho g\]
Since this weight is the thrust acting on an area A to Y
hydrostatic pressure at Y i.e.
\[\Pr essure=\frac{F}{A}=\frac{Ah\rho g}{A}\]
Pressure\[=h\rho g\]
hydrostatic pressure = density x acceleration due to gravity x depth
Pressure exerted by a liquid at a point inside the liquid is directly proportional to:
(i) the depth of the point from the free surface of liquid and
(ii) density of the liquid and
(iii) acceleration due to gravity
Remember:
The upward force exerted by a liquid on a body which is immersed in the liquid is known as the upl hrust or buoyant force.
The tendency of a fluid to exert an upward force on an object placed in it is called buoyancy.
Factors on which up thrust or buoy and force depends:
(i) the size or volume of the body immersed in a liquid and
(ii) the density of the liquid in which the body is immersed.
Mathematical Expression for upward thrust: Consider a cylindrical body ABCD of height h and cross sectional area a, completely immersed in a liquid of density\[\rho \].
Let the upper surface AB of the body be at a depth Ai below the free surface of the liquid and lower surface CD of the body below the free surface of the liquid.
1.\[{{P}_{1}}={{h}_{1}}\rho g(At\,depth\,{{h}_{1}})\]
2.\[{{P}_{2}}={{h}_{2}}\rho g(At\,depth\,{{h}_{2}})\]
As \[{{h}_{2}}>{{h}_{1}},{{P}_{2}}>{{P}_{1}}\] because we know that the pressure inside a liquid increases with depth.

Fig.16.1
So the net pressure P in the upward direction is
\[P={{P}_{2}}-{{P}_{1}}\]
\[P={{h}_{2}}\rho g-{{h}_{1}}\rho g\]
\[P=({{h}_{2}}-{{h}_{1}})\rho g\]
\[P=h\rho g\] \[[\because {{h}_{2}}-{{h}_{1}}=h]\]
\[\because \] Force = Pressure \[\times \]Area \[\left[ \because \Pr essure=\frac{F}{A} \right]\]
\[\therefore \] Upward thrust \[=h\rho ga\]
Upward thrust =\[V\rho g\]
or Upward thrust = mg = W \[\left[ Density=\frac{Mass}{Volume} \right]\]
Here W = weight of the liquid displaced by the immersed part of the body
Important properties of buoyant force:
(1) Buoyant force is directly proportional to the volume of the body submerged in the fluid.
(2) Buoyant force is directly proportional to the density of the fluid in which the body is submerged.
Example: On pushing two plastic balls of same size, one in water and the other in salt solution then we observe that our hands experience more buoyant force in salt solution than in case of water. This is because density of salt solution is more than that of water.
(3) Buoyant force is directly proportional to the acceleration due to gravity.
Remember: We experience more Buoyant force on the earth than on the moon.
\[{{g}_{moon}}\approx 1.63m{{s}^{2}}\]
\[{{g}_{earth}}\approx 9.8m{{s}^{2}}\]
(4) Buoyant force is inversely proportional to the temperature of the fluid.
Do You Know
As the temperature of a fluid increases, its volume also increases. Hence, its density decreases.
A body, fully or partly immersed in a liquid, experiences a resultant upward force or up thrust which acts in a direction opposite to the weight of the body. Therefore, the body appears to be lighter so long as it is immersed in a liquid. Its apparent reduction in weight is equal to the height of the liquid it displaces. This fact was first discovered by Archimedes, the Greek philosoher.
Archimedes’ Principle states that: "When a body is wholly or partially immersed in a liquid at rest, it experiences an upthrust (or an apparent loss in weight) which is equal to the weight of the liquid displaced by the body.
Do You Know
In floatation it is the density of the body which matters and not that of its material.
This principle is used to design:
(i) the ships and submarines
(ii) the hydrometers to find the densities of liquids
(iii) the lactometers to test the purity of milk.
(1) Floatation of ice-bergs: Icebergs are huge pieces of ice floating in sea water. The density of ice \[\left( \text{about}0.9gc{{m}^{-}}^{3} \right)\]is less than the density of sea-water (about 1.04 g cm- 3) so they displace more weight of sea water than their own weight. Hence, the ice-bergs float in this sea water.
(2) Floatation offish and whales: The fish and whales have an air bladder in their bodies.
The air in the bladder decreases the average density of the fish. So they float in sea water. To dive into the sea, they force out the air from the bladder. Now the density of the fish increases and hence it sinks into the sea water.
(3) Floatation of man: The average density of the human body with empty lungs is \[1.07\text{ }g/c{{m}^{3}}\]while with lungs filled with air, it is \[1.00\text{ }g/c{{m}^{3}}\], so the water of this sea offers a greater buoyant force. So the chances of drowning in the Dead sea are very less. A man can easily swim with his shoulders above the sea water all the time.
Relative density of a substance\[\text{=}\frac{\text{Density}\,\text{of}\,\text{substance}}{\text{Density}\,\text{of}\,\text{water}}\]
\[\text{=}\frac{\text{Mass}\,\text{of}\,\text{substance/Volume}\,\text{of}\,\text{substance}}{\text{Mass}\,\text{of}\,\text{water/Volume}\,\text{of}\,\text{water}}\]
\[\text{=}\frac{\text{Mass}\,\text{of}\,\text{substance}}{\text{Mass}\,\text{of}\,\text{water}}\text{ }\!\!\times\!\!\text{ }\frac{\text{Volume}\,\text{of}\,\text{water}}{\text{Volume}\,\text{of}\,\text{substance}}\]
If volume of substance = Volume of water
Relative density of substance\[\text{=}\frac{\text{Mass}\,\text{of}\,\text{any}\,\text{volume}\,\text{of}\,\text{the}\,\text{substance}}{\text{Mass}\,\text{of}\,\text{an}\,\text{equal}\,\text{volume}\,\text{of}\,\text{water}}\]
Hence, relative density of a substance is defined as the ratio of the mass of any volume of the substance to the mass of an equal volume of water.
Since mass of any substance is directly proportional to its weight, so relative density of the substance can also be defined as:
Relative density 01 a substance \[\text{=}\frac{\text{Weight of any volume of the substance}}{\text{Weight of an equal volume of water}}\]
Relative Density has no unit as it is a ratio.
Relative density of a substance is a number of times the given substance is heavier than the equal volume of water.
The relative density of iron = 7.9, it means, iron is 7.9 times heavier than equal volume of water
Remember: \[1gc{{m}^{-3}}=1000kg{{m}^{-3}}\].
Chapter at a Glance
Mathematically,
\[F=G\frac{{{m}_{1}}{{m}_{2}}}{{{r}^{2}}}\]
where G is universal gravitational constant.
\[{{a}_{c}}=\frac{1}{{{r}^{2}}}\]
\[g=\frac{GM}{{{R}^{2}}}\]
(i) shape of the earth
(ii) height
(iii) depth and
(iv) latitude on the earth.
\[M=\frac{g{{R}^{2}}}{G}\]
(i)\[v=u+gt\]
(ii)\[s=ut+\frac{1}{2}g{{t}^{2}}\]
(ii)\[{{v}^{2}}={{u}^{2}}+2gs\]
In Cartesian sign convention, the value of g is always taken negative.
\[\text{=}\frac{\text{Mass}\,\text{of}\,\text{any}\,\text{volume}\,\text{aof}\,\text{substance}}{\text{Mass}\,\text{of}\,\text{the}\,\text{same}\,\text{volume}\,\text{of}\,\text{water}}\]
\[\text{=}\frac{\text{Weight}\,\text{of}\,\text{any}\,\text{volume}\,\text{of}\,\text{substance}}{\text{Weight}\,\text{of}\,\text{an}\,\text{equal}\,\text{volume}\,\text{of}\,\text{water}}\]
You need to login to perform this action.
You will be redirected in
3 sec
