9th Class Science Work and energy Energy

       Energy

The word energy is used daily in our daily life. In science we give the word a definite and specific meaning. The energy is defined as the ability to do the work. Thus, the unit of energy is same as that of work. That is the unit of energy is joule. 1 joule is the energy required to do the work of 1 joule. The larger unit of energy is kilojoule.

1 kj = 1000 joule

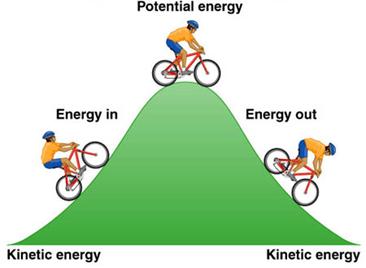
The object which possess energy can exert a force on another object. When this happens, the energy is transferred from the former to the latter. The second object may move as it receives energy and therefore do some work. There are different forms of energy. The different forms of energy includes mechanical energy, heat energy, chemical energy, electrical energy, and light energy. The mechanical energy is of two form: the kinetic energy and the potential energy.

          Kinetic Energy

It is defined as the energy possessed by the body, by the virtue of its motion.

Thus, every object in motion possess energy irrespective of the object moving speedly or slowly. We can derive the relation for the kinetic energy. Let us consider an object of mass 'm' moving with a uniform velocity' u'. When a constant force 'F' is applied on the object it is displaced through a distance 'S' in the direction of force. The work done by the force is given by,

W = F x S

Let the work done on the object changes its velocity from 'u' to V which produces an acceleration of 'a', then from third equation of motion we have,

\[{{v}^{2}}-{{u}^{2}}=2as\]

Or,          \[S=\frac{{{v}^{2}}-{{u}^{2}}}{2a}\]

From Newtons second law, we have

F = ma

Therefore, work done is

W=ma \[\times \] S

Or, W=max v -u

Or, \[W=\,ma\times \,\left( \frac{{{v}^{2}}-{{u}^{2}}}{2a} \right)\]

Or, \[W=\,m\times \,\left( \frac{{{v}^{2}}-{{u}^{2}}}{2} \right)\]

If the object is starting from rest then u=0, hence the work done is given by

\[W=\frac{1}{2}m\times {{v}^{2}}\]

Since this work done is equal to the change in kinetic energy, so the kinetic energy is given by

\[K.E.=\frac{1}{2}\,m\times {{v}^{2}}\]

             Potential Energy

It is defined as the energy possessed by the body, by the virtue of its shape and position.

When an object is raised to a certain height its energy increases. This is because of work done on the object against gravity, when it is being raised to a certain height. The energy possessed in such object is called the gravitational potential energy.

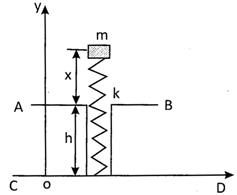
Let us consider an object of mass 'm' raised to a height of 'h' from the surface of ground. The force required to raise the object to a height 'h' is equal to the weight of the object 'mg', where g is the acceleration due to gravity. Thus, the work done is given by

Work = force x displacement = mg x h = mgh

Hence the potential energy is equal to, P.E. = mgh

The potential energy has many uses such as generation of hydroelectricity.

The SI unit of potential energy is joule (J).

It is a scalar quantity.

        Find the energy possessed by a ball of mass 550 gm rolling on the surface with a speed of 25 m/sec.

(a) 120.896 joules

(b) 132.875 joules

(c) 171.875 joules

(d) 150.965 joules

(e) None of these

Answer: (c)

         An object of mass 2 kg is raised to a height of 0.102 meters. Find the energy required to raise the object to the height.

(a) 2.5892 joules

(b) 1.9992 joules

(c) 1.7175 joules

(d) 1.5065 joules

(e) None of these

Answer: (b)

        Calculate the work done in lifting an object of mass 0.5 kg to a height of 1.5 meters from the ground.

(a) 8.02 joules

(b) 6.28 joules

(c) 7.98 joules

(d) 7.35 joules

(e) None of these

Answer: (d)

         A batsman hits the ball of mass 250 gm with his bat and the ball leaves the bat with the speed of 10 m/s. Find the work done by the bat on the ball.

(a) 10.25 joules

(b) 9.75 joules

(c) 12.5 joules

(d) 8.35 joules

(e) None of these

Answer: (c)

        A ball of mass 1 kg is thrown upward with a speed of 10 m/s. Find the potential energy of the ball when it reaches the highest point.

(a) 50 joules

(b) 25 joules

(c) 75 joules

(d) 90 joules

(e) None of these

Answer: (a)

            Relation between Kinetic Energy and Momentum

The kinetic energy and momentum (p) are related to each other.

\[K.E.=\frac{1}{2}\,m{{v}^{2}}\]

But,        \[p=mv\]

\[K.E.=\frac{1}{2}\,m\,{{\left( \frac{p}{m} \right)}^{2}}\,K.E.=\frac{{{p}^{2}}}{2m}\]