Railways Basic Science and Engineering Mass, Weight and Density

Mass, Weight and Density

Mass

The mass (m) of a body of matter is quantitative measure of its inertia i.e., its resistance to a change in the state of rest or motion of the body, when a force is applied.

• SI unit of mass is the kilogram (kg). It is a scalar quantity.
• The greater the mass of a body, the smaller the rate of change in motion.

Inertia is the property of a mass which resists change from its states of rest or motion.

• The inertia of an object refers to the reluctance of the object to start moving if it is stationary in the first instance or the reluctance of the object to stop moving if it rs moving in the first instance.
• When a body of matter is stationary, it needs a force to make it start moving. The bigger the mass, the bigger the force needed. We say that masses have inertia: a reluctance to start moving.

Volume (V) is defined as the amount of space occupied by a three-dimensional object as measured in cubic units.

• SI unit of volume is meter cube .It is a scalar quantity.

Weight

The weight of an object is defined as the force of gravity on the object and may be calculated as the mass times the acceleration of gravity, w = mg. Since the weight is a force, its SI unit is the

Newton.

For an object in free fall, so that gravity is the only force acting on it,

Then the expression for weight follows from Newton's second law.

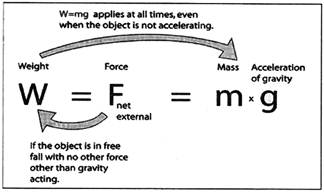
The value of g allows us to determine the net gravity force if it were in freefall and that net gravity force is the weight. Another approach is to consider "g" to be the measure of the intensity of

Ac gravity field in Newtons/kg at our location. We can view the weight as a measure of the mass in kg times the intensity of the gravity field, 9.8 Newton's/kg under standard conditions.

Density

Density (p) is defined as the mass of a substance per unit volume. 

• SI unit of density is kilograms per meter cube \[(kg\,\,{{m}^{-3}})\] It is a scalar quantity.
• Another common unit of density is \[g\,\,c{{m}^{-3}}g\,\,c{{m}^{-3}}.1000\,kg\,{{m}^{-3}}\]\[=1\,\,g\,\,c{{m}^{-3}}1000\,kg\,{{m}^{-3}}=1\,\,g\,\,c{{m}^{-3}}\]
• \[\rho =m\,V\]
• The density of a substance does not change as we move from place to place as the mass and volume does not depend on the gravitational acceleration of the point that the object is at.

There are two kinds of density, "weight density" and "mass density". We will only use mass density and when we say: "density", its means "mass density".

The metric system was designed so that water will have a density of one gram per cubic centimeter or 1000 kilograms per cubic meter. Lead is about 10 times as dense as water and Styrofoam is about one tenth as dense as water.

Fluid Density

Mass per unit volume is defined as density. So density at a point of a fluid is represented as

\[\rho =\underset{\Delta V\to 0}{\mathop{\lim }}\,\frac{\Delta m}{\Delta V}=\frac{dm}{dV}\]

where m is the mass and v is the volume of the fluid. Density is a positive scalar quantity.

SI unit: \[kg/{{m}^{3}}\]

Dimensions: \[[M{{L}^{-3}}{{T}^{0}}]\]

• For a solid body volume and density will be same as that of its constituent substance of equal mass.

i.e.\[{{M}_{body}}={{M}_{sub}}\]then\[{{V}_{body}}={{V}_{sub}}\]and\[{{\rho }_{body}}={{\rho }_{sub}}.\]

But for a hollow body or body with air gaps

\[{{M}_{body}}={{M}_{sub}}\]and\[{{V}_{body}}>{{V}_{sub}}\]then\[{{\rho }_{body}}<{{\rho }_{sub}}\]

• If \[{{m}_{1}}\] mass of liquid of density \[{{\rho }_{1}}\] and \[{{m}_{2}}\] mass of liquid of density \[{{\rho }_{2}}\] are mixed then,

\[{{M}_{MIX}}={{m}_{1}}+{{m}_{2}}\]and\[{{V}_{MIX}}={{V}_{1}}+{{V}_{2}}=\]\[\frac{{{m}_{1}}}{{{\rho }_{1}}}+\frac{{{m}_{2}}}{{{\rho }_{2}}}\]

\[\therefore \]      \[\rho \,\,mix=\frac{M\,\,mix}{V\,\,mix}=\frac{{{m}_{1}}+{{m}_{2}}}{\underset{\rho 1}{\mathop{\underline{{{m}_{1}}}}}\,+\underset{\rho 2}{\mathop{\underline{{{m}_{2}}}}}\,}\]

• If same masses are mixed, i.e.\[{{m}_{1}}={{m}_{2}}=m\] then

\[\rho \,\,mix=\frac{2{{\rho }_{1}}{{\rho }_{2}}}{{{\rho }_{1}}+{{\rho }_{2}}}\](harmonic mean of individual densities)

• If \[{{V}_{1}}\]volume of liquid of density \[{{\rho }_{1}}\]and\[{{V}_{2}}\] volume of liquid of density \[{{\rho }_{2}}\]are mixed then

\[{{V}_{MIX}}={{V}_{1}}+{{V}_{2}}\] and,

\[{{M}_{MIX}}={{m}_{1}}+{{m}_{2}}={{\rho }_{1}}{{V}_{1}}+{{\rho }_{2}}{{V}_{2}}\]

\[\therefore \]      \[\rho \,\,mix=\frac{M\,\,mix}{V\,\,mix}=\frac{{{\rho }_{1}}{{V}_{1}}+{{\rho }_{2}}{{V}_{2}}}{{{V}_{1}}+{{V}_{2}}}\]

• If same volumes are mixed, i.e.\[{{V}_{1}}={{V}_{2}}=V\] then,

\[\rho \,\,mix=\frac{{{\rho }_{1}}+{{\rho }_{2}}}{2}\](arithmetic mean of individual densities)

Specific Weight or Weight Density (W)

It is defined as the ratio of the weight of the fluid to its volume or the weight acting per unit volume of the fluid.

Specific weight, \[W=\frac{Weight}{Volume}\]

\[W=\frac{mg}{V}=\left[ \frac{m}{V} \right]g=\rho g\]

S I Unit:\[N/{{m}^{3}}\] Dimensions:\[[M{{L}^{-2}}{{T}^{-2}}]\]

Specific weight of pure water at \[4{}^\circ C\] is \[9.81\,\,kN/{{m}^{3}}\]

Relative Density

It is defined as the ratio of the density of the given fluid to the density of pure water at \[4{}^\circ C\]

Density of given liquid

Relative density (R.D).\[=\frac{Density\,\,of\,\,given\,\,liquid}{Density\,\,of\,\,pure\,\,water\,\,at\,\,4{}^\circ C}\]

The density of water is maximum at \[4{}^\circ C\] and is equal to \[1.0\times {{10}^{3}}kg{{m}^{-3}}\]

Relative density or specific gravity is a unitless and dimensionless positive scalar physical quantity.

Being a dimensionless/unitless quantity R.D. of a substance is same in SI and CGS system.

Specific Gravity

It is defined as the ratio of the specific weight of the given fluid to the specific weight of pure water at\[4{}^\circ C\],

Specific gravity

\[=\frac{Specific\,\,weight\,\,of\,\,given\,liquid}{Specific\,\,weight\,\,of\,\,pure\,\,water\,\,at\,\,4{}^\circ C(9.81kN/{{m}^{3}})}\]

\[=\frac{{{\rho }_{\gamma }}\times g}{{{\rho }_{w}}\times g}=\frac{{{\rho }_{\gamma }}}{{{\rho }_{w}}}\]=R.D. of the liquid

Thus specific gravity of a liquid is numerically equal to the relative density of that liquid and for calculation purposes they are used interchangeably.