A) \[{{y}^{2}}-4y-21=0\]
B) \[{{y}^{2}}+4y-21=0\]
C) \[{{y}^{2}}-4y+21=0\]
D) \[{{y}^{2}}+4y+21=0\]
Correct Answer: A
Solution :
Let the lines are \[y={{m}_{1}}x+{{c}_{1}}\] and \[y={{m}_{2}}x+{{c}_{2}}\] since pair of straight lines parallel to x-axis, \\[{{m}_{1}}={{m}_{2}}=0\] and the lines will be \[y={{c}_{1}}\]and \[y={{c}_{2}}\] Given circle is \[{{x}^{2}}+{{y}^{2}}-6x-4y-12=0\], centre (3, 2) and radius = 5.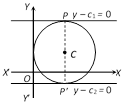 Here, the perpendicular drawn from centre to the lines are CP and \[C{P}'\]. \[CP=\frac{2-{{c}_{1}}}{\sqrt{1}}=\pm 5\] Þ \[2-{{c}_{1}}=\pm 5\] \[{{c}_{1}}=7\] and \[{{c}_{1}}=-3\] Hence the lines are \[y-7=0,\,y+3=0\] i.e.,\[(y-7)\,(y+3)=0\] \ Pair of straight lines is \[{{y}^{2}}-4y-21=0\].
Here, the perpendicular drawn from centre to the lines are CP and \[C{P}'\]. \[CP=\frac{2-{{c}_{1}}}{\sqrt{1}}=\pm 5\] Þ \[2-{{c}_{1}}=\pm 5\] \[{{c}_{1}}=7\] and \[{{c}_{1}}=-3\] Hence the lines are \[y-7=0,\,y+3=0\] i.e.,\[(y-7)\,(y+3)=0\] \ Pair of straight lines is \[{{y}^{2}}-4y-21=0\].
You need to login to perform this action.
You will be redirected in
3 sec
