question_answer

If the lines \[{{l}_{1}}x+{{m}_{1}}y+{{n}_{1}}=0\] and \[{{l}_{2}}x+{{m}_{2}}y+{{n}_{2}}=0\] cuts the axes at con-cyclic points, then

A)            \[{{l}_{1}}{{l}_{2}}={{m}_{1}}{{m}_{2}}\]                    

B)            \[{{l}_{1}}{{m}_{1}}={{l}_{2}}{{m}_{2}}\]

C)            \[{{l}_{1}}{{l}_{2}}+{{m}_{1}}{{m}_{2}}=0\]              

D)            \[{{l}_{1}}{{m}_{2}}={{l}_{2}}{{m}_{1}}\]

Correct Answer: A

Solution :

           \[{{P}_{1}}\equiv \left( -\frac{{{n}_{1}}}{{{l}_{1}}},\ 0 \right)\],\[{{P}_{2}}\equiv \left( 0,\ \frac{-{{n}_{1}}}{{{m}_{1}}} \right)\],\[{{P}_{3}}\equiv \left( -\frac{{{n}_{2}}}{{{l}_{2}}},\ 0 \right)\] and                    \[{{P}_{4}}\equiv \left( 0,\ -\frac{{{n}_{2}}}{{{m}_{2}}} \right)\]               \[\{\angle {{P}_{1}}{{P}_{2}}{{P}_{3}}=\angle {{P}_{1}}{{P}_{4}}{{P}_{3}}\}\]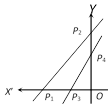                    Now, \[{{m}_{12}}=-\frac{{{l}_{1}}}{{{m}_{1}}},\ {{m}_{23}}=-\frac{{{n}_{1}}}{{{n}_{2}}}.\frac{{{l}_{2}}}{{{m}_{1}}},\ {{m}_{14}}=-\frac{{{n}_{2}}}{{{n}_{1}}}.\frac{{{l}_{1}}}{{{m}_{2}}}\],                              \[{{m}_{34}}=-\frac{{{l}_{2}}}{{{m}_{2}}}\]                    \[\tan \theta =\frac{-\frac{{{l}_{1}}}{{{m}_{1}}}+\frac{{{n}_{1}}{{l}_{2}}}{{{n}_{2}}{{m}_{1}}}}{1+\frac{{{n}_{1}}{{l}_{1}}{{l}_{2}}}{{{n}_{2}}m_{1}^{2}}}\] and \[\tan \varphi =\frac{-\frac{{{n}_{2}}{{l}_{1}}}{{{n}_{1}}{{m}_{2}}}+\frac{{{l}_{2}}}{{{m}_{2}}}}{1+\frac{{{n}_{2}}{{l}_{1}}{{l}_{2}}}{{{n}_{1}}m_{2}^{2}}}\]                    Now, \[\tan \theta =\tan \varphi \Rightarrow {{m}_{1}}{{m}_{2}}={{l}_{1}}{{l}_{2}}\]                    Aliter: Line \[{{l}_{1}}x+{{m}_{1}}y+{{n}_{1}}=0\] cuts x and y-axes in \[A\text{ }\left( -\frac{{{n}_{1}}}{{{l}_{1}}},\ 0 \right)\],\[B\text{ }\left( 0,\ -\frac{{{n}_{1}}}{{{m}_{1}}} \right)\] and line \[{{l}_{2}}x+{{m}_{2}}y+{{n}_{2}}=0\] cuts axes in \[C\text{ }\left( -\frac{{{n}_{2}}}{{{l}_{2}}},\ 0 \right)\], \[D\text{ }\left( 0,\ \frac{-{{n}_{2}}}{{{m}_{2}}} \right)\].                    So AC and BD are chords along x and y-axes intersecting at origin O. Since A, B, C, D are concyclic, so OA.OC = OB.OD                    or \[\left| \text{ }\left( -\frac{{{n}_{1}}}{{{l}_{1}}} \right)\text{ }\left( -\frac{{{n}_{2}}}{{{l}_{2}}} \right)\text{ } \right|=\left| \text{ }\left( -\frac{{{n}_{1}}}{{{m}_{1}}} \right)\text{ }\left( -\frac{{{n}_{2}}}{{{m}_{2}}} \right)\text{ } \right|\]                    or \[|{{l}_{1}}{{l}_{2}}|\ =\ |{{m}_{1}}{{m}_{2}}|\]                    So \[{{l}_{1}}{{l}_{2}}={{m}_{1}}{{m}_{2}}\]is correct among the given choices, which is given in (a).