-
question_answer1)
A convex lens of focal length 15 cm placed coaxially in front of a convex mirror. The lens is 5 cm from apex of mirror. When an object is placed on the axis at a distance of 20 cm from the lens, it is found that image coincides with object, radius of curvature of mirror is
A)
65 cm done
clear
B)
60 cm done
clear
C)
55 cm done
clear
D)
75 cm done
clear
View Solution play_arrow
-
question_answer2)
A 35 mm film is to be projected on a 20 m wide screen situated at a distance of 40 m from the film-projector. Calculate the focal length of projection lens.
A)
70 mm done
clear
B)
35 mm done
clear
C)
40 mm done
clear
D)
20 mm done
clear
View Solution play_arrow
-
question_answer3)
A thin convergent glass lens \[\mu =1.5\] has a power of + 5.0 D. When this lens is immersed in a liquid of refractive index \[{{\mu }_{1}}\] it acts as a divergence lens of focal length 100 cm. The value of \[{{\mu }_{1}}\] should be
A)
3/2 done
clear
B)
4/3 done
clear
C)
5/3 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer4)
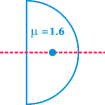
A plastic hemisphere has a radius of curvature of 8 cm and an index of refraction of 1.6. On the axis halfway between the plane surface and the spherical one (4 cm from each) is a small object O. The distance between the two images when viewed along the axis from the two sides of the hemisphere is approximately
A)
1.0 cm done
clear
B)
1.5 cm done
clear
C)
3.75 cm done
clear
D)
2.5 cm done
clear
View Solution play_arrow
-
question_answer5)
Two plano-convex lenses each of focal length 10 cm & refractive index \[\frac{3}{2}\] are placed as shown. In the space left, water \[\left( R.l=\frac{4}{3} \right)\] is filled. The whole arrangement is in air. The optical power of the system is (in diopters)

A)
6.67 done
clear
B)
- 6.67 done
clear
C)
33.3 done
clear
D)
- 33.3 done
clear
View Solution play_arrow
-
question_answer6)
Convex side of a convexo-concave lens is silvered and on its principle axis a point object is moving toward it from concave side then
A)
its image will continuously move toward the lens done
clear
B)
its image may continuously move toward the lens done
clear
C)
its image will always be real done
clear
D)
its image may be real done
clear
View Solution play_arrow
-
question_answer7)
The human eye can be regarded as a single spherical refracting surface of curvature of radii 7.8 mm. If a parallel beam of light comes to focus at 3.075 cm behind the refracting surface, the refractive index of the eye is
A)
1.34 done
clear
B)
1 done
clear
C)
1.5 done
clear
D)
1.86 done
clear
View Solution play_arrow
-
question_answer8)
Two point light sources are 24 cm apart. Where should a convex lens of focal length 9 cm be put in between them from one source so that the images of both the sources are formed at the same place
A)
6 cm done
clear
B)
9 cm done
clear
C)
12 cm done
clear
D)
15 cm done
clear
View Solution play_arrow
-
question_answer9)
An equiconvex lens has a power of 5 diopter. If it is made of glass of refractive index 1.5 then the radius of the curvature of each surface will be
A)
20 cm done
clear
B)
10 cm done
clear
C)
5 cm done
clear
D)
zero done
clear
View Solution play_arrow
-
question_answer10)
An electron revolves in air in a circle in a plane perpendicular to the principal axis. The air has a uniform magnetic field parallel to the principal axis and of magnitude 2 tesla with centre of circle at a distance 10 cm from the pole of the spherical curved glass \[(\mu =1.5)\] surface of radius of curvature 10 cm as shown in figure. An observer from P sees radius of circle to be 10 mm. The linear momentum of electron is

A)
\[0.4\times {{10}^{-21}}kg-m/s\] done
clear
B)
\[0.8\times {{10}^{-21}}kg-m/s\] done
clear
C)
\[1.6\times {{10}^{-21}}kg-m/s\] done
clear
D)
\[2.4\times {{10}^{-21}}kg-m/s\] done
clear
View Solution play_arrow
-
question_answer11)
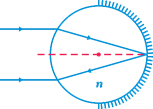
A transparent cylinder has its right half polished so as to act as a mirror. A paraxial light ray is incident from left that is parallel to principal axis, exits parallel to the incident ray as shown. The refractive index n of the material of the cylinder is:
A)
1.2 done
clear
B)
1.5 done
clear
C)
1.8 done
clear
D)
2.0 done
clear
View Solution play_arrow
-
question_answer12)
A lens is placed between a source of light and a wall. It forms images of area \[{{A}_{1}}\] and \[{{A}_{2}}\] on the wall, for its two different positions. The area of the source of light is
A)
\[\sqrt{\left( {{A}_{1}}{{A}_{2}} \right)}\] done
clear
B)
\[\left( {{A}_{1}}{{A}_{2}} \right)/2\] done
clear
C)
\[\frac{{{\left( \sqrt{{{A}_{1}}}+\sqrt{{{A}_{2}}} \right)}^{2}}}{2}\] done
clear
D)
\[{{\left[ \frac{l}{{{A}_{1}}}+\frac{l}{{{A}_{2}}} \right]}^{-1}}\] done
clear
View Solution play_arrow
-
question_answer13)
Light rays from a very distant source travel along the \[+x\] direction. Two identical thin lenses with focal length \[f>0\] and their optical axis along x, sit, one at \[x=0\] and the other at \[x=d<f\]. The rays focus at \[x=\]
A)
\[d+\frac{f(f-d)}{2f-d}\] done
clear
B)
\[d-\frac{f(f-d)}{d}\] done
clear
C)
\[d+\frac{f(f-d)}{2(f+d)}\] done
clear
D)
\[d+\frac{{{f}^{2}}}{2(f-d)}\] done
clear
View Solution play_arrow
-
question_answer14)
A convex lens forms a real image three times larger than the object on a screen. Object and screen are moved until the image becomes twice the size of the object. If the shift of the object is 6 cm. The shift of screen is:
A)
36 cm done
clear
B)
72 cm done
clear
C)
18 cm done
clear
D)
9 cm done
clear
View Solution play_arrow
-
question_answer15)
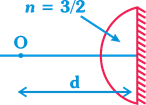
A plano-convex lens of focal length 10 cm is silvered at its plane face. The distance d at which an object must be placed in order to get its image on itself is:
A)
5 cm done
clear
B)
20 cm done
clear
C)
10 cm done
clear
D)
2.5 cm done
clear
View Solution play_arrow
-
question_answer16)
A convex lens of focal length \[f\] is placed somewhere in between an object and a screen. The distance between the object and the screen is\[x\]. If the magnification produced by the lens is \[m,\] the focal length of the lens is
A)
\[\frac{mx}{{{(m+1)}^{2}}}\] done
clear
B)
\[\frac{mx}{{{(m-1)}^{2}}}\] done
clear
C)
\[\frac{{{(m+1)}^{2}}}{mx}\] done
clear
D)
\[\frac{{{(m-1)}^{2}}}{mx}\] done
clear
View Solution play_arrow
-
question_answer17)
A boy is trying to start a fire by focusing sunlight on a piece of paper using an equiconvex lens of focal length 10 cm. The diameter of the sun is \[1.39\times {{10}^{9}}\,m\] and its mean distance from the earth is \[1.5\times {{10}^{11}}\text{ }m\]. What is the diameter of the sun's image on the paper?
A)
\[9.2\times {{10}^{-4}}m\] done
clear
B)
\[6.5\times {{10}^{-4}}m\] done
clear
C)
\[6.5\times {{10}^{-5}}m\] done
clear
D)
\[12.4\times {{10}^{-4}}m\] done
clear
View Solution play_arrow
-
question_answer18)
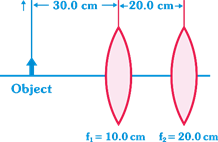
Two converging lenses are placed 20.0 cm apart. as shown in figure. If the first lens has a focal length of 10.0 cm and the second has a focal length of 20.0 cm, locate the final image formed of an object 30.0 cm in front of the first lens.
A)
6.67 cm left done
clear
B)
6.67 cm right done
clear
C)
15.0 cm left done
clear
D)
15.0 cm right done
clear
View Solution play_arrow
-
question_answer19)
A convex lens is made up of three different materials as shown in the figure. For a point object places on its axis, the number of images formed are:

A)
5 done
clear
B)
1 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer20)
A parallel beam of light is incident on a lens of focal length 10 cm. A parallel slab of refractive index 1.5 and thickness 3 cm is placed on the other side of the lens. The Nature of the final image from the lens slab combination is: (Assume rays paraaxial)
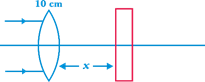
A)
At Distance of 11 cm and Image is virtual if \[X=12\text{ }cm\] done
clear
B)
At Distance of 11 cm and Image is virtual if \[X=14\text{ }cm\] done
clear
C)
At the Distance of 11 cm and Image is Virtual if \[X=16\text{ }cm\] done
clear
D)
All the above done
clear
View Solution play_arrow
-
question_answer21)
A light ray is incident on a transparent sphere of radius R as shown below, refractive index of the sphere (Assume paraxial incidence) is
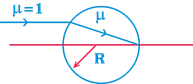
A)
1 done
clear
B)
3/2 done
clear
C)
2/3 done
clear
D)
2 done
clear
View Solution play_arrow
-
question_answer22)
When the plane surface of a planoconvex lens of refractive index 1.5 is silvered, it behaves like concave mirror of focal length 30 cm. When it? convex surface is silvered, it will behave like a concave mirror of focal length
A)
10 cm done
clear
B)
20 cm done
clear
C)
30 cm done
clear
D)
45 cm done
clear
View Solution play_arrow
-
question_answer23)
A convex spherical refracting surface with radius R separates a medium having RI 5/2 from air. As an object is moved towards the surface far away from the surface along central axis, its image
A)
Changes from real to virtual when it is at a distance of R from the surface done
clear
B)
Changes from virtual to real when it is at a distance of R from the surface. done
clear
C)
Changes from real to virtual when it is at a distance no. of \[\frac{2R}{3}\] from the surface done
clear
D)
Changes from virtual to real when it is at a distance of \[\frac{2R}{3}\] from the surface done
clear
View Solution play_arrow
-
question_answer24)
A combination of two thin lenses with focal lengths \[{{f}_{1}}\] and \[{{f}_{2}}\] respectively forms an image of distant object at distance 60 cm when lenses are in contact. The position of this image shifts by 30 cm towards the combination when two lenses are separated by 10 cm. The corresponding values of \[{{f}_{1}}\] and \[{{f}_{2}}\] are
A)
\[30\text{ }cm,\text{ }-60\text{ }cm\] done
clear
B)
\[20\text{ }cm,\text{ }-30\text{ }cm\] done
clear
C)
\[15\text{ }cm,\text{ }-20\text{ }cm\] done
clear
D)
\[12\text{ }cm,\text{ }-15\text{ }cm\] done
clear
View Solution play_arrow
-
question_answer25)
| Direction: A point object O is placed at the origin of coordinate system. An equi-convex thin lens\[({{\mu }_{g}}=1.5)\] of focal length \[f=20\,cm\]in air is placed so that its principal axis is along x-axis. Now the lens is cut at the middle (along the principal axis) and upper half is shifted along x-axis and y-axis by 20 cm and 2 mm respectively and right side of lower half is filled with water \[({{\mu }_{\omega }}=4/3)\] |
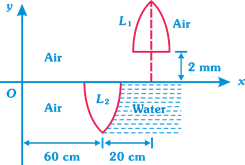 |
| Total number of images formed by the combination will be |
A)
1 done
clear
B)
2 done
clear
C)
3 done
clear
D)
4 done
clear
View Solution play_arrow
-
question_answer26)
| Direction: A point object O is placed at the origin of coordinate system. An equi-convex thin lens\[({{\mu }_{g}}=1.5)\] of focal length \[f=20\,cm\]in air is placed so that its principal axis is along x-axis. Now the lens is cut at the middle (along the principal axis) and upper half is shifted along x-axis and y-axis by 20 cm and 2 mm respectively and right side of lower half is filled with water \[({{\mu }_{\omega }}=4/3)\] |
 |
| Coordinates of the image produced by the lens \[{{L}_{1}}\] will be |
A)
\[\left( \frac{320}{3}cm,\frac{4}{3}mm \right)\] done
clear
B)
\[\left( \frac{160}{3}cm,\frac{8}{3}mm \right)\] done
clear
C)
\[\left( \frac{320}{3}cm,\frac{8}{3}mm \right)\] done
clear
D)
\[\left( \frac{160}{3}cm,\frac{4}{3}mm \right)\] done
clear
View Solution play_arrow
-
question_answer27)
| Direction: A point object O is placed at the origin of coordinate system. An equi-convex thin lens\[({{\mu }_{g}}=1.5)\] of focal length \[f=20\,cm\]in air is placed so that its principal axis is along x-axis. Now the lens is cut at the middle (along the principal axis) and upper half is shifted along x-axis and y-axis by 20 cm and 2 mm respectively and right side of lower half is filled with water \[({{\mu }_{\omega }}=4/3)\] |
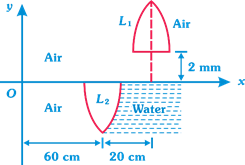 |
| Coordinates of the image produced by the lens \[{{L}_{2}}\] will be |
A)
140 cm, 0 done
clear
B)
140 cm, 20 done
clear
C)
70 cm, 0 done
clear
D)
140 cm, 30 done
clear
View Solution play_arrow
-
question_answer28)
A thin linear object of size 1 mm is kept along the principal axis of a convex lens of focal length 10 cm. The object is at 15 cm from the lens. The length of the image is:
A)
1 mm done
clear
B)
4 mm done
clear
C)
2 mm done
clear
D)
8 mm done
clear
View Solution play_arrow
-
question_answer29)
A convex lens is placed in contact with a mirror as shown. If the space between them is filled with water, its power will

A)
decrease done
clear
B)
increase done
clear
C)
remain unchanged done
clear
D)
increase or decrease depending of the foe length done
clear
View Solution play_arrow
-
question_answer30)
An air bubble in a glass sphere having 4 cm diameter appears 1 cm from surface nearest to eye when looked along diameter. If \[_{a}{{\mu }_{g}}=1.5,\] the distance of bubble from refracting surface is
A)
1.2 cm done
clear
B)
3.2 cm done
clear
C)
2.8 cm done
clear
D)
1.6 cm done
clear
View Solution play_arrow
-
question_answer31)
A wire mesh consisting of very small squares is viewed at a distance of 8 cm through a magnifying converging lens of focal length 10 cm, kept close to the eye. The magnification produced by the lens is
A)
5 done
clear
B)
8 done
clear
C)
10 done
clear
D)
20 done
clear
View Solution play_arrow
-
question_answer32)
A point object is placed at a distance of 30 cm along the principal axis of a convex lens of focal length 20 cm and aperture 4 cm. The lens is cut by a plane parallel to its principal axis and both the identical pieces are inverted and placed in contact at their vertex. The distance between the images formed is
A)
4 cm done
clear
B)
8 cm done
clear
C)
12 cm done
clear
D)
16 cm done
clear
View Solution play_arrow
-
question_answer33)
When an object is at distances x and y from a lens, a real image and a virtual image is formed respectively having same magnification. The focal length of the lens is:
A)
\[\frac{x+y}{2}\] done
clear
B)
\[x-y\] done
clear
C)
\[\sqrt{xy}\] done
clear
D)
\[x+y\] done
clear
View Solution play_arrow
-
question_answer34)
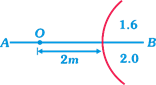
In the figure shown a point object O is placed in air. A spherical boundary of radius of curvature 1.0 m separates two media. AB is principal axis. The refractive index above AB is 1.6 and below AB is 2.0. The separation between the images formed due to refraction at spherical surface is:
A)
12 m done
clear
B)
20 m done
clear
C)
14 m done
clear
D)
10 m done
clear
View Solution play_arrow
-
question_answer35)
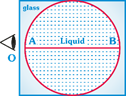
The observer 'O' sees the distance AB as infinitely large. If refractive index of liquid is \[{{\mu }_{1}}\] and that of glass is \[{{\mu }_{2}}\], then \[\frac{{{\mu }_{1}}}{{{\mu }_{2}}}\] is:
A)
2 done
clear
B)
1/2 done
clear
C)
4 done
clear
D)
None of these done
clear
View Solution play_arrow
