A) \[\frac{3}{4}\]
B) \[\frac{4}{3}\]
C) \[\frac{1}{2}\]
D) \[\frac{2}{3}\]
Correct Answer: B
Solution :
Let diameter of sphere \[AE=2r\] Let radius of cone is x and height is y \ \[AD=y\] since \[B{{D}^{2}}=AD.DE\]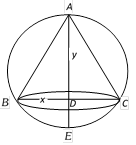 |
You need to login to perform this action.
You will be redirected in
3 sec
