question_answer

If \[{{I}_{1}}=\int\limits_{0}^{\frac{\pi }{2}}{\cos (\sin \,\,x)dx;{{I}_{2}}=\int\limits_{0}^{\frac{\pi }{2}}{\sin (\cos \,\,x)dx}}\] and \[{{I}_{3}}=\int\limits_{0}^{\frac{\pi }{2}}{\cos x\,\,dx,}\] then

A) \[{{I}_{1}}>{{I}_{3}}>{{I}_{2}}\]

B) \[{{I}_{3}}>{{I}_{1}}>{{I}_{2}}\]

C) \[{{I}_{1}}>{{I}_{2}}>{{I}_{3}}\]

D) \[{{I}_{3}}>{{I}_{2}}>{{I}_{1}}\]

Correct Answer: A

Solution :

[a] \[{{I}_{1}}=\int\limits_{0}^{\frac{\pi }{2}}{\cos (\sin \,\,x)dx}\]

\[{{I}_{2}}=\int\limits_{0}^{\frac{\pi }{2}}{sin(cos\,\,x)dx}\]

\[{{I}_{3}}=\int\limits_{0}^{\frac{\pi }{2}}{cos\,x\,dx}\]

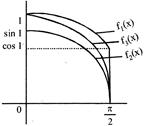
Let \[{{f}_{1}}(x)=\cos (\sin \,\,x),{{f}_{2}}(x)=\sin (\cos \,\,x),\]

\[{{f}_{3}}(x)=\cos \,\,x\]

If \[x>0\], then \[\sin x<x\]

\[\Rightarrow \] for \[0<x<\frac{\pi }{2},\sin (\cos \,\,x)<\cos \,\,x\]

Also, \[0<x<\frac{\pi }{2}\] then \[\sin x<x\]

\[\Rightarrow \cos (\sin \,\,x)>\cos \,\,x\]

\[\therefore \cos (\sin \,\,x)>\cos \,\,x>\sin (\cos \,\,x)\] if \[0<x<\frac{\pi }{2}\]

\[\therefore {{I}_{1}}>{{I}_{3}}>{{I}_{2}}\]