| Factorise the following: |
| (a) \[{{x}^{4}}-{{y}^{4}}\] |
| (b) \[16{{x}^{4}}-81\] |
| (a) Simplify : \[3x\left( 4x-5 \right)+3\]and find its value |
| (i) x = 3 (ii) x = \[\frac{1}{2}\]: |
| (b) Simplify: \[a\left( {{a}^{2}}+a+1 \right)+5\]and find its value for (a) a = 0 (b) a = 1 (c) \[a\text{ }=-1.\] |
| Verify that \[-\text{ }\left( -\text{ }x \right)\text{ }=\text{ }x\]for |
| (a) \[x=\frac{11}{15}\] |
| (b) \[x=-\frac{13}{17}\] |
| Numbers 1 to 10 are written on ten separate slips (one number on one slip) kept in a box and mixed |
| well. One slip chosen from the box without looking into it. What is the probability of |
| (a) getting a number 6 ? |
| (b) getting a number less than 6? |
| (c) getting a number greater than 6? |
| (d) getting a 1-digit number? |
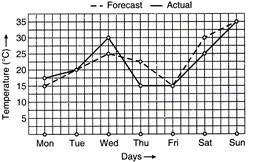
| The following graph shows the temperature forecast and the actual temperature for each day of a week. |
| (a) On which day was the forecast temperature the same as the actual temperature? |
| (b) What was the maximum forecast temperature during the week? |
| (c) What was the minimum actual temperature during the week? |
| (d) On which day did the actual temperature differ the most from the forecast temperature? |
 |
| Calculate the amount and compound interest on. |
| (a) Rs. 10,800 for 3 years at \[12\frac{1}{2}%\] per annum compounded annually. |
| (b) Rs.18, 000 for \[2\frac{1}{2}\] years at 10% per annum compounded annually. |
| Column I | Column II | |
| 1. | X and y vary inversely to each other | A. \[\frac{x}{y}\]= Constant |
| 2. | Mathematical representation of inverse variation of quantities p and q | B. y will increase in proportion |
| 3. | Mathematical representation of direct variation of quantities m and n | C. xy= constant |
| 4. | When =5,y=2.5and when y=5,x=10 | D. \[p\propto \frac{1}{q}\] |
| 5. | When x = 10, y = 5 and when x = 20, y = 2.5 | E. y will decrease in proportion |
| 6. | x and y vary directly with each other | E x and y directly proportional |
| 7. | If x and y vary inversely then on decreasing x | G. \[m\text{ }\alpha \,n\] |
| 8. | If z and y vary directly then on decreasing x. | H. x and y vary inversely |
| \[I.p\propto q\] | ||
| \[J.m\propto \frac{1}{n}\] |
| Using \[\left( x+a \right)\left( x+b \right)={{x}^{2}}+\left( a+b \right)x+\text{ }ab,\]find |
| (a) \[103\times 104~\] |
| (b) \[5.1\times 5.2~\] |
| (c) \[103\times 98~\] |
| (d) \[9.7\times 9.8\] |
You need to login to perform this action.
You will be redirected in
3 sec
