A) \[\frac{{{B}_{Y}}}{{{B}_{X}}}=1\]
B) \[\frac{{{B}_{Y}}}{{{B}_{X}}}=2\]
C) \[\frac{{{B}_{Y}}}{{{B}_{X}}}=\frac{1}{2}\]
D) \[\frac{{{B}_{Y}}}{{{B}_{X}}}=\frac{1}{4}\]
Correct Answer: C
Solution :
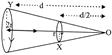
Magnetic induction at 0 due to coil Y is given by,\[{{B}_{Y}}=\frac{{{\mu }_{0}}}{4\pi }\times \frac{2\pi I{{(2r)}^{2}}}{{{\left[ {{(2r)}^{2}}{{d}^{2}} \right]}^{3/2}}}\] ??(1) Similarly, the magnetic induction at 0 due to coil X is given by \[{{B}_{X}}=\frac{{{\mu }_{0}}}{4\pi }\times \frac{2\pi I{{r}^{2}}}{{{\left[ {{r}^{2}}+{{(d/2)}^{2}} \right]}^{3/2}}}\] ??(2) From eq.(1) & (2) \[\frac{{{B}_{Y}}}{{{B}_{X}}}=\frac{1}{2}\]You need to login to perform this action.
You will be redirected in
3 sec
