question_answer

A man of mass m stands on a frame of mass M. He pulls on a light rope, which passes over a pulley. The other end of the rope is attached to the frame. For the system to be in equilibrium, what force must the man exert on the rope?

A) \[\frac{1}{2}(M+m)g\]                      

B) \[(M+m)g\]                 

C) \[(M-m)g\]                   

D) \[(M+2m)g\]

Correct Answer: A

Solution :

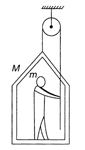
Let T = tension in the rope = Force exerted by the nan on the rope = Force exerted by the rope on he man.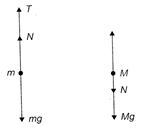      N = normal reaction between man and frame. For equilibrium, \[T+N=mg,\,T=N+Mg.\] Solving the above relations, we get, \[T=\frac{1}{2}(M+m)g\] Hence, the correction option is [a].