question_answer

Show that the refractive index of the material of a prism is given by \[\mu =\frac{\sin \frac{(A+{{\delta }_{m}})}{2}}{\sin \left( \frac{A}{2} \right)}\] where, the symbols have their usual meanings, Or Define magnifying power of a telescope. Write its expression. A small telescope has an objective lens of focal length 150 cm and an eyepiece off focal length 5 cm. If this telescope is used to view a 100 m high tower 3 km away, find the height of the final image when it is formed 25 cm away from the eyepiece.

Answer:

            Consider a prism ABC of refractive index, \[\mu .\] A light ray PQ is incident on face AB at an angle of incidence, i and refracted at an angle, \[{{r}_{1}}.\] It strikes on face AC at an angle, \[{{r}_{2}}\] and emerges at angle, e. The angle of deviation is \[\delta .\] 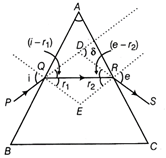                        A prism of refractive index, \[\mu \]             Here,     \[\angle DQR=(i-{{r}_{1}})\]                         \[\angle DRQ=(e-{{r}_{2}})\]             For \[\Delta DQR,\delta \] is exterior angle             \[\therefore \]      \[\delta =(i-{{r}_{1}})+(e-{{r}_{2}})\]             or         \[\delta =(i+e)-({{r}_{1}}+{{r}_{2}})\]              ?(i)             In cyclic quadrilateral AQER,             \[\therefore \]      \[\angle A+\angle E=180{}^\circ \]                     ?(ii)             In triangle QER,                         \[{{r}_{1}}+{{r}_{2}}+\angle E=180{}^\circ \]                        ?(iii)             From Eqs. (ii) and (iii), we get                         \[\angle A={{r}_{1}}+{{r}_{2}}\]                                 ?(iv)             Substituting value in Eq. (i). we get                         \[\delta =(i+e)-\angle A\]                         ?(v) For minimum angle of deviation \[({{\delta }_{m}}),\] \[\delta ={{\delta }_{m}}\] and \[i=e,\] \[{{r}_{1}}={{r}_{2}}=r\]          [assume] From Eq. (iv), we get \[\angle A=r+r\] or \[r=\frac{\angle A}{2}\]          \[=\frac{A}{2a}\]                      ?(vi) From Eq. (v), we get, \[{{\delta }_{m}}=i+i-\angle A\] or         \[i=\frac{\angle A+{{\delta }_{m}}}{2}=\frac{A+{{\delta }_{m}}}{2}\]             (vii) If \[\mu \] is refractive index of the material of the prism, then \[\mu =\frac{\sin i}{\sin r}\] Substituting the values of / and r. we get \[\therefore \]      \[\mu =\frac{\sin \left( \frac{A+{{\delta }_{m}}}{2} \right)}{\sin \left( \frac{A}{2} \right)}\] Or The magnifying power of a telescope is equal to the ratio of the visual angle subtended at the eye by final image formed at least distance of distinct vision to the visual angle subtended at naked eye by the object at infinity. When final image is at D. Magnifying power, \[M=\frac{{{f}_{o}}}{{{f}_{e}}}\left( 1+\frac{{{f}_{e}}}{D} \right)\] In normal adjustment, \[M=\frac{{{f}_{o}}}{{{f}_{e}}}\] For telescope Focal length of objective lens, \[{{f}_{o}}=150\,cm\] Focal length of eye lens, \[{{f}_{e}}=5\,cm\] When final image forms at D = 25 cm Magnification,    \[=M=\frac{-{{f}_{o}}}{{{f}_{e}}}\left( 1+\frac{{{f}_{e}}}{D} \right)\]                         \[=\frac{-150}{5}\left( 1+\frac{5}{25} \right)=\frac{-150}{5}\times \frac{6}{5}\] \[M=-36\] Let height of final image be h cm. \[\Rightarrow \]   \[\tan \beta =\frac{h}{25}\] \[\beta \]= visual angle formed by final image at eye. \[\alpha \]=visual angle subtended by object at objective. \[\tan \alpha =\frac{100m}{3000m}=\frac{1}{30}\] But,      \[M=\frac{\tan \beta }{\tan \alpha }\]             \[-36=\frac{\left( \frac{h}{25} \right)}{\left( \frac{1}{30} \right)}=\frac{h}{25}\times 30\]             \[-36=\frac{6h}{5}\]             \[h=\frac{-36\times 5}{6}=-30\,cm\] Negative sign indicate inverted image.