A) \[({{F}_{1}}+{{F}_{2}})/2\]
B) \[({{F}_{1}}-{{F}_{2}})\]
C) \[({{F}_{1}}+{{F}_{2}})\]
D) \[2\,({{F}_{1}}+{{F}_{2}})\]
Correct Answer: C
Solution :
Let r be the perpendicular distance of \[{{F}_{1}},{{F}_{2}}\] and \[{{F}_{3}}\] from O as shown in figure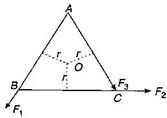 The torque of force \[{{F}_{3}}\] about O is clockwise, while torque due to \[{{F}_{1}}\] and \[{{F}_{2}}\] are anticlockwise. For total torque to be zero about O, we must have \[{{F}_{1}}r+{{F}_{2}}r-{{F}_{3}}r=0\] \[\Rightarrow {{F}_{3}}={{F}_{1}}+{{F}_{2}}\]
The torque of force \[{{F}_{3}}\] about O is clockwise, while torque due to \[{{F}_{1}}\] and \[{{F}_{2}}\] are anticlockwise. For total torque to be zero about O, we must have \[{{F}_{1}}r+{{F}_{2}}r-{{F}_{3}}r=0\] \[\Rightarrow {{F}_{3}}={{F}_{1}}+{{F}_{2}}\]
You need to login to perform this action.
You will be redirected in
3 sec
