A) \[a\]
B) \[2a\]
C) \[3a\]
D) \[4a\]
Correct Answer: D
Solution :
Since,\[\Delta SPM\]is an equilateral triangle.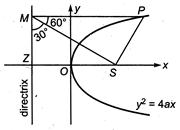 Therefore, \[SP=PM=SM\] \[\therefore \] \[\angle PMZ=90{}^\circ \] and \[\angle PMS=60{}^\circ \] \[\therefore \] \[\angle SMZ=30{}^\circ \] Now, in right angle\[\Delta SMZ\] \[\sin 30{}^\circ =\frac{SZ}{SM}\] \[\Rightarrow \] \[\frac{1}{2}=\frac{2a}{SM}\] \[\Rightarrow \] \[SM=4a\] \[\Rightarrow \] \[PM=4a\] \[(\because PM=SM)\]
Therefore, \[SP=PM=SM\] \[\therefore \] \[\angle PMZ=90{}^\circ \] and \[\angle PMS=60{}^\circ \] \[\therefore \] \[\angle SMZ=30{}^\circ \] Now, in right angle\[\Delta SMZ\] \[\sin 30{}^\circ =\frac{SZ}{SM}\] \[\Rightarrow \] \[\frac{1}{2}=\frac{2a}{SM}\] \[\Rightarrow \] \[SM=4a\] \[\Rightarrow \] \[PM=4a\] \[(\because PM=SM)\]
You need to login to perform this action.
You will be redirected in
3 sec
