A) \[{{m}_{0}}\]
B) \[2{{m}_{0}}\]
C) \[{{m}_{0}}/2\]
D) \[{{m}_{0}}/4\]
Correct Answer: A
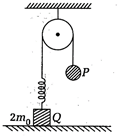
Solution :
The block will experience maximum upward force, when the ball P is at its lowest position (x). Energy conservation gives \[mgx=\frac{1}{2}k{{x}^{2}}\]or \[x=2mg/k\] ?(i) For the block Q to leave contact \[kx=2\,{{m}_{0}}g\] Solving Eqs. (i) and (ii), we get \[m=2{{m}_{0}}/2={{m}_{0}}\]You need to login to perform this action.
You will be redirected in
3 sec
