question_answer

Let \[A=[{{a}_{ij}}]\] and \[B=[{{b}_{ij}}]\] be two \[3\times 3\] real matrices such that \[{{b}_{ij}}={{(3)}^{(i+j2)}}\,{{a}_{ji}},\]where i, j = 1, 2, 3. If the determinant of B is 81, then the determinant of A is         [JEE MAIN Held on 07-01-2020 Evening]

A) 1/9      

B) 1/81

C) 3                     

D) 1/3

Correct Answer: A

Solution :

[a]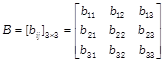 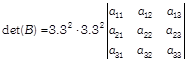\[\therefore \,\,\,{{3}^{4}}={{3}^{6}}\cdot \det \,(A)\] \[\therefore \,\,\,\det \,(A)=\frac{1}{{{3}^{2}}}=\frac{1}{9}\]