A) \[\frac{128}{3}\]
B) \[\frac{125}{3}\]
C) \[\frac{127}{3}\]
D) \[\frac{124}{3}\]
Correct Answer: A
Solution :
[a] For point of intersections \[4{{x}^{2}}=8x+12\] \[{{x}^{2}}2x3=0\] \[\therefore \,\,\,\,\,x=\,1,3\]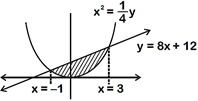 The required area =\[\int_{-1}^{3}{(8x+12-4{{x}^{2}})}\,dx\] \[=\,4\left( 2\cdot \frac{{{x}^{2}}}{2}+3x-\frac{{{x}^{3}}}{3} \right)_{-\,1}^{3}\] \[=\,4\,\left\{ (9+9-9)-\left( 1-3+\frac{1}{3} \right) \right\}\] \[=\frac{128}{3}\,square\,units\]
The required area =\[\int_{-1}^{3}{(8x+12-4{{x}^{2}})}\,dx\] \[=\,4\left( 2\cdot \frac{{{x}^{2}}}{2}+3x-\frac{{{x}^{3}}}{3} \right)_{-\,1}^{3}\] \[=\,4\,\left\{ (9+9-9)-\left( 1-3+\frac{1}{3} \right) \right\}\] \[=\frac{128}{3}\,square\,units\]
You need to login to perform this action.
You will be redirected in
3 sec
