question_answer

Let the tangents drawn from the origin to the circle, \[{{x}^{2}}+{{y}^{2}}8x4y+16=0\]touch it at the points A and B. The \[{{(AB)}^{2}}\]is equal to    [JEE MAIN Held on 07-01-2020 Evening]

A) \[\frac{64}{5}\]                      

B) \[\frac{52}{5}\]

C) \[\frac{56}{5}\]          

D) \[\frac{32}{5}\]

Correct Answer: A

Solution :

[a] Equation of chord of contact is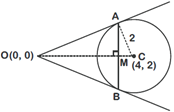 \[x\cdot 0+y\cdot 0-4(x+0)-2(y+0)+16=0\] \[\therefore \,\,\,\,\,\,2x+y-8=0\] \[\therefore \]  Length of \[CM=\left[ \frac{2\cdot 4+2-8}{\sqrt{{{2}^{2}}+{{1}^{2}}}} \right]=\frac{2}{\sqrt{5}}\] units. \[\therefore \,\,\,AM=BM=\sqrt{4-\frac{4}{5}}=\sqrt{\frac{16}{5}}\] \[\therefore \]    Length of chord of contact (AB)  \[=\frac{8}{\sqrt{5}}\] \[\therefore \]  Square of length of chord of Contact\[={{\left( \frac{8}{\sqrt{5}} \right)}^{2}}=\frac{64}{5}\].