10th Class Mathematics Circles Introduction

      Introduction 

Circle is defined as the locus of a point which is at a constant distance from a fixed point. The fixed point is called the centre of the circle and the fixed distance is called the radius of the circle.  

      Tangent to a circle

A tangent to a circle is a line which intersects the circle at exactly one point. The point where the tangent intersects the circle is known as the point of contact.  

           Properties of tangent to a circle

Following are some properties of tangent to a circle:

• A tangent to a circle is perpendicular to the radius through the point of contact.
• A line drown through the end-point of a radius and perpendicular to it is a tangent to the circle.
• The length of he two tangents drawn from an external point to a circle are equal.
• If two tangents are drawn to a circle from an external point, then they subtend equal angles at the centre.
• If two tangents are drawn to a circle from an external point, then they are equally inclined to the segment, joining the centre to that point.  

From the above points we conclude that in the following figure;

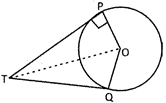
\[\angle OPT=\angle OQT={{90}^{o}},\,\angle POT=\angle QOT\] \[\angle QTO=\angle OTP\,and\,PT\,=\,QT\]  

Two tangents PT and QT are drawn to a circle with centre 0 from an external point as shown in the following figure, then:

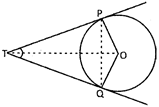
(a) \[\angle QTP=\angle QPO\]                    

(b) \[\angle QTP=2\angle QPO\]

(c) \[\angle QTP=3\angle QPO\]                  

(d) \[\angle QTP={{90}^{o}}\]

(e) None of these  

Answer: (b)  

Explanation          

In the given figure, we have

TP = TO.            [tangents drawn from an external point are equal in length]

\[\Rightarrow \,\,\angle TPQ=\,\angle TPQ\]

\[In\,\angle QTQ,\,we\,\,have\]

\[\angle TPQ+\angle TQP+PTQ={{180}^{o}}\]

\[\Rightarrow \,\angle TPQ={{90}^{o}}-\frac{1}{2}\angle PTQ\]

\[\Rightarrow \,\frac{1}{2}\angle PTQ={{90}^{o}}-\angle TPQ\]     .... (i)             

Also, \[\angle OPT={{90}^{o}}\]             

\[\Rightarrow \,\angle OPQ={{90}^{o}}-\angle TPQ\]            .... (ii)

From (i) and (ii), we get

\[\frac{1}{2}\angle PTQ=\angle OPQ\Rightarrow \angle PTQ=2\angle OPQ\]