10th Class Mathematics Circles Circle

CIRCLE

 

INTRODUCTION

FUNDAMENTALS       

• A circle is the locus of points in a plane which are at a fixed distance from a fixed point.
• The fixed point is called the centre of the circle and the fixed distance is the radius of the circle and is denoted as ‘r’.

• In the figure, OR is a radius of the circle ‘r’.
• PQ is a diameter of the circle. OP and OQ are also the radii of the circle.

• PQ = diameter (d) = 2r                                
• The perimeter of the circle is called the circumference of the circle (C).
• The circumference of the circle is n times the diameter, i.e. \[C=\pi d=2\pi r\]
• Interior and exterior points of a circle.

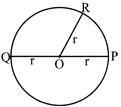
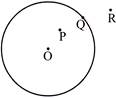
In the figure with centre O, P, Q and R are three points as shown above lying in the plane of the circle. The points O and P are in the interior of the circle. The point Q is located on the circumference of the circle, whereas point R is located outside the circle.

As \[OP<r,P\]is a point in the interior of the circle.

If \[OQ=r,Q\]is a point on the circumference of the circle and is said to belong to the circle.

As \[OR>r,R\]is a point in the exterior of the circle.

 

CHORD

The line segment joining any two points on the circumference of a circle is called chord of the circle. In the figure \[\overline{PQ}\] and \[\overline{RS}\]are the chords.                                  

• PQ passes through centre O, hence it is a diameter of the circle. Diameter is the longest chord of the circle. It divides the circle into two equal parts and each part is called semi-circle.
• Now, we will study certain theorems and also commit them to our memory.

 

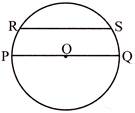
Theorems and properties on chords

Theorem 1

The perpendicular bisector of a chord of a circle passes through the centre of the circle. 

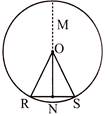
Given: RS is a chord of a circle with centre O. N is the midpoint of chord PQ.                                                    

• Draw a line \[\bot \]to RS passing through ‘N’.
• O will lie on line NOM.

 

Theorem 2                                                   

One and only one circle exists through three non – collinear points. 

                

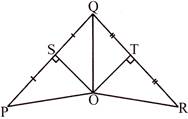
Given: P, Q and R are three non – collinear points as shown in the adjoining figure:

• In order to locate the centre, join PQ and QR.
• Draw \[\bot \] bisectors of PQ and a QR and let them meet at ‘O’ as show below.
• Now, OP = OQ = OR = r = radius and you can draw the circle.

Theorem 3

Two equal chords of a circle are equidistant from the centre of the circle.   

   

 

• In the figure, PQ and RS are chords of equal length.
• Draw OT \[\bot \]to PQ and OU \[\bot \] to RS.
• Then OT= OU

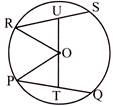
The converse of the above theorem, is also true, i.e., two chords which are equidistant from the centre of a circle are equal in length.

 

Property: Longer chords are closer to the centre and shorter chords are farther away from the centre.

Observe the figure:                          

• \[PQ>RS>TU>VW\]
• Diameter PQ is the longest chord and is at zero distance from centre.
• RS is one of the longer chords and its distance from centre – \[O{{O}_{1}}\]
• TU is comparatively shorter whereas VW is comparatively the shortest.
• The distance follow the trend\[O{{O}_{1}}<O{{O}_{2}}<O{{O}_{3}}\].

 

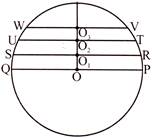
Angles Subtended by Equal Chords at the centre

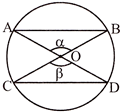
Theorem 4

Equal chords subtend equal angles at the centre of the circle, i.e. angle \[\alpha \]= angle \[\beta \]

Angles Subtended by an Arc

Property 1

Angles subtended by an arc at any point on the rest of the circle are equal.

• Let the arc be PXQ
• Let arc PXQ subtend \[\angle PRQ=9\] and \[\angle PSQ=\phi \]
• Then, \[\theta =\phi \]

 

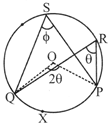
Property 2

Angle subtended by an arc at the centre of a circle is double the angle subtended by it at any point on the remaining part of the circle.

• In the previous figure, angle subtended by arc PXQ at the centre is \[\angle POQ=2\phi =2\phi \]

 

Cyclic Quadrilateral

If all the four vertices of a quadrilateral lie on a circle, it is called a cyclic quadrilateral. In the given figure, the four vertices, P, Q, R, S lie on the circle. Thus, PQRS is a cyclic quadrilateral.

 

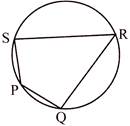
Theorem 5

The opposite angles of a cyclic quadrilateral are supplementary.       

       

• Consider \[\angle S\left( \angle PSR \right)\] and\[\angle Q\left( \angle PQR \right)\].
• Chord PR subtends \[\angle S\]at circumference and \[\angle POR\](larger angle) at the centre. Hence, \[\angle POR\](larger) \[=2\angle S=\theta \](see figure)
• Similarly, PR subtends \[\angle Q\] at circumference and \[\angle POR\] (Smaller angle \[\phi \]) at the centre \[\angle POR\] (smaller) \[=2\angle Q=\phi \]
• Therefore, \[\theta +\phi =360{}^\circ \] (angle around a point)

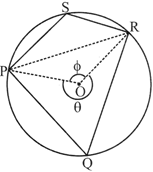
\[\Rightarrow \]\[2\angle S+2\angle Q=360{}^\circ \] \[\Rightarrow \] \[\angle S+\angle Q=180{}^\circ \]

• Similar construction will give \[\angle P+\angle R=180{}^\circ \]

 

 Theorem 6

The exterior angle of a cyclic quadrilateral is equal to the interior opposite angle.

 

• This follows from previous theorem as \[\alpha +\gamma =180{}^\circ \]and \[\gamma =180{}^\circ -\theta \] \[\Rightarrow \] \[\alpha =\theta \] (see figure below).
• \[\theta +\phi =360{}^\circ \]
• \[2\angle S+2\angle Q=360{}^\circ \]
• \[\angle S+\angle Q=180{}^\circ \]

 

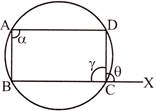
Tangents

When a line and a circle are drawn in the same plane, we have the following cases.

1. The line and the circle may not intersect at all, as shown in the figure below,

(i) Then PQ is called secant of the circle.

(ii) Then AB is called the tangent of the circle at P.

2. The line may intersect the circle at two points as shown in Figure.
3. The line may touch the circle at only one point as shown in Figure.

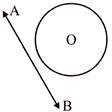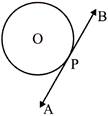(i)           (ii)      (iii)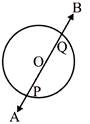

(a) At any point on a circle, only one tangent can be drawn.

(b) From any given external point, two tangents can be drawn to a circle.

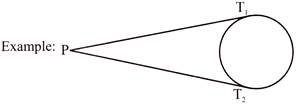
(c) From any point inside a circle, no tangent can be drawn to the circle.

 

Theorem 7

The tangent at any point on a circle is perpendicular to the radius through the point of contact.

 

 

Theorem 8

Statement of the Theorem:

Two tangents drawn to a circle from an external point are equal in length.

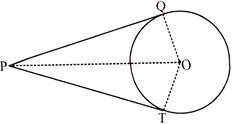
Theorem 9

Statement of the Theorem

If two chords of a circle intersect each other, then the products of the lengths of their segments are equal.

OP. OQ = OR. OS

 

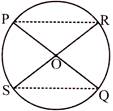
Alternate Segment and its Angles

Let PQ be a chord in a circle with centre O. A tangent is drawn to the circle at P. Chord PQ makes two angles with the tangents \[\angle QPY\] and \[\angle QPX\]. Chord PQ divides the circle into two segments PRQ and PSQ. The segments PRQ and PSQ are called alternate segment to angles \[\angle QPY\] and \[\angle QPX\] respectively.

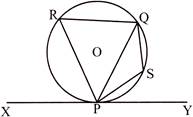
Theorem 10: (Alternate Segment Theorem)

If a line touches the circle at a point and if a chord is drawn from the point of contact, then the angles formed between the chord and the tangent are equal to the angles in the alternate segments.                                

\[\angle QPY=\angle PRQ\] and\[\text{ }\angle QPX=\angle PSQ\]

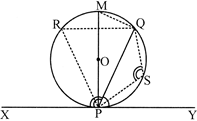
Converse of Alternate Segment Theorem

A line is drawn through the end point of a chord of a circle such that the angle formed between the line and the chord is equal to the angle subtended by the chord in the alternate segment. Then, the line is tangent to the circle at the point.

 

Common tangent to Two circle in a plane

If the same line is tangent to two circles drawn in the same plane, then the line is called a common tangent to the circles. The distance between the point of contacts is called the length of the common tangent.

 

In the figure, PQ is a common tangent to the circles with centres, \[{{C}_{1}}\] and \[{{C}_{2}}\]. The length PQ is the length of the common tangent.

           

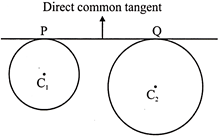(i)               (ii)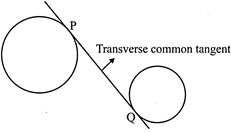

 

In Figure (i), we observe that both the circles lies on the same side of PQ. In this case, PQ is a direct common tangent whereas in figure (ii), we notice that the two circles lie on either side of PQ. Hence, PQ is a transverse common tangent.

 

1. The number of common tangents to the circles when one circle lies inside the other (Without touching each other), is zero.

                                                                                                                                                                        

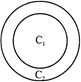
    2.  The number of common tangents to two circles touching internally is one.

 

                                             

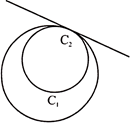
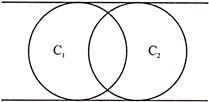
    3.    The common tangents to two intersecting circles, are TWO direct common tangents, as shown below.

                                

 

 

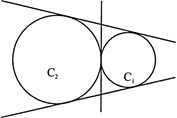
4.        The common tangents to two circle touching externally, are TWO direct common tangents and ONE transverse common tangent. (Total = 3)

 

          

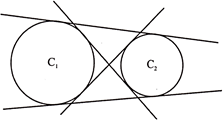
5.            The common tangents to non – intersecting circles are TWO direct common tangents and TWO transverse common tangents. (Total =4, see figure below).

                              

Note on Common Tangents

1. When two circles touch each other internally or externally, then the line joining the centres is perpendicular to the tangent drawn at the point of contact of the two circles.

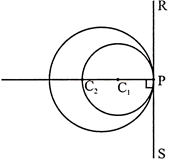
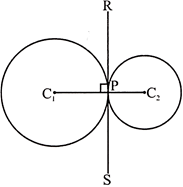
Case 1: Two circles with centres \[{{C}_{1}}\] and \[{{C}_{2}}\]touch each other internally at \[P.{{C}_{1}}{{C}_{2}}\] P is the line drawn through the centres and RS is the common tangent at P.

\[\therefore \]\[~{{C}_{1}}{{C}_{2}}P\] is \[\bot \] to RS.

Case 2: Two circles with centres \[{{C}_{1}}\] and \[{{C}_{2}}\] touch each other externally at P. Here, \[{{C}_{1}}{{C}_{2}}\] is perpendicular to XY.

 

 

Case 3: The direct common tangents to two circles of equal radii are parallel to each other.

 

 

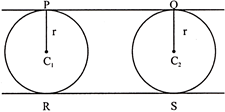
Mathematical Statement:

Let there be two circles of equal radii ‘r’ have centres \[{{C}_{1}}\] and \[{{C}_{2}}\] Also, let PQ and RS be the direct common tangents. Then\[PQ\parallel RS\].