JEE Main & Advanced Mathematics Vector Algebra Application of Vectors in 3-dimensional Geometry

(1) Direction cosines of \[\mathbf{r}=a\mathbf{i}+b\mathbf{j}+c\mathbf{k}\] are \[\frac{a}{|\mathbf{r}|},\,\frac{b}{|\mathbf{r}|},\,\frac{c}{|\mathbf{r}|}\].

 

(2) Incentre formula : The position vector of the incentre of \[\Delta ABC\] is \[\frac{a\,\mathbf{a}+b\,\mathbf{b}+c\,\mathbf{c}}{a+b+c}\].

 

(3) Orthocentre formula : The position vector of the orthocentre of \[\left| \,\begin{matrix}

   {{a}_{1}} & {{a}_{2}} & {{a}_{3}} & 1  \\

   {{b}_{1}} & {{b}_{2}} & {{b}_{3}} & 1  \\

   {{c}_{1}} & {{c}_{2}} & {{c}_{3}} & 1  \\

   {{d}_{1}} & {{d}_{2}} & {{d}_{3}} & 1  \\

\end{matrix}\, \right|\,=0\] is \[\frac{\mathbf{a}\tan A+\mathbf{b}\tan B+\mathbf{c}\tan C}{\tan A+\tan B+\tan C}\].

 

 

(4) Vector equation of a straight line passing through a fixed point with position vector \[\mathbf{a}\] and parallel to a given vector \[\mathbf{b}\] is \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\].

 

 

(5) The vector equation of a line passing through two points with position vectors \[\mathbf{a}\] and \[\mathbf{b}\] is \[\mathbf{r}=\mathbf{a}+\lambda (\mathbf{b}-\mathbf{a})\].

 

 

(6) If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\lambda {{\mathbf{b}}_{2}}\] are coplanar, then \[[{{\mathbf{a}}_{1}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]\] and the equation of the plane containing them is \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{1}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]\] or \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]\].

 

 

 

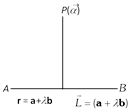
(7) Perpendicular distance of a point from a line : Let L is the foot of perpendicular drawn from \[P(\vec{\alpha })\] on the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\]. Since \[\mathbf{r}\] denotes the position vector of any point on the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\]. So, let the position vector of \[\vec{L}\] be \[\mathbf{a}+\lambda \mathbf{b}\].

 

 

Then \[\overrightarrow{PL}=\mathbf{a}-\overrightarrow{\alpha }+\lambda \mathbf{b}=(\mathbf{a}-\overrightarrow{\alpha })-\left( \frac{(\mathbf{a}-\overrightarrow{\alpha })\mathbf{b}}{|\mathbf{b}{{|}^{2}}} \right)\mathbf{b}\]

 

 

The length PL, is the magnitude of\[\overrightarrow{PL}\], and required length of perpendicular.

 

 

 

 

 

 

 

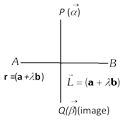
(8) Image of a point in a straight line : Let \[Q(\overrightarrow{\beta })\] is the image of P in \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\], then, \[\overrightarrow{\beta }=2\mathbf{a}-\left( \frac{2(\mathbf{a}-\overrightarrow{\alpha }).\mathbf{b}}{|\mathbf{b}{{|}^{2}}} \right)\mathbf{b}-\overrightarrow{\alpha }\]

 

 

(9) Shortest distance between two parallel lines : Let \[{{l}_{1}}\] and \[{{l}_{2}}\] be two lines whose equations are \[{{l}_{1}}:\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[{{l}_{2}}:\mathbf{r}={{\mathbf{a}}_{2}}+\mu {{\mathbf{b}}_{2}}\] respectively.

 

 

Then, shortest distance

 

 

\[PQ=\left| \frac{({{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{\mathbf{2}}})\,.\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})}{|{{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}}|} \right|=\left| \frac{[{{\mathbf{b}}_{1}}\text{ }{{\mathbf{b}}_{\mathbf{2}}}\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})]}{|{{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}}|} \right|\]

 

 

Shortest distance between two parallel lines : The shortest distance between the parallel lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda \mathbf{b}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\mu \mathbf{b}\] is given by \[d=\frac{|({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})\times \mathbf{b}|}{|\mathbf{b}|}\].

 

 

If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda {{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\mu {{\mathbf{b}}_{2}}\] intersect, then the shortest distance between them is zero.

 

 

Therefore, \[[{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}\,({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})]=0\]

 

 

\[\Rightarrow \]\[[({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}})\,\,{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]=0\]\[\Rightarrow \]\[({{\mathbf{a}}_{2}}-{{\mathbf{a}}_{1}}).({{\mathbf{b}}_{1}}\times {{\mathbf{b}}_{2}})=0\].

 

 

(10) If the lines \[\mathbf{r}={{\mathbf{a}}_{1}}+\lambda \,{{\mathbf{b}}_{1}}\] and \[\mathbf{r}={{\mathbf{a}}_{2}}+\lambda \,{{\mathbf{b}}_{2}}\] are coplanar, then \[[{{\mathbf{a}}_{1}}{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}{{\mathbf{b}}_{1}}{{\mathbf{b}}_{2}}]\] and the equation of the plane containing them is \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{1}}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]\] or \[[\mathbf{r}\,{{\mathbf{b}}_{1}}\,{{\mathbf{b}}_{2}}]=[{{\mathbf{a}}_{2}}\,{{\mathbf{b}}_{\mathbf{1}}}\,{{\mathbf{b}}_{\mathbf{2}}}]\].

 

 

(11) Vector equation of a plane through the point \[A(\mathbf{a})\] and perpendicular to the vector \[\mathbf{n}\] is \[(\mathbf{r}-\mathbf{a}).\mathbf{n}=0\] or \[\mathbf{r}.\mathbf{n}=\mathbf{a}.\mathbf{n}\] or \[\mathbf{r}\,.\,\mathbf{n}=d\], where \[d=\mathbf{a}\,.\,\mathbf{n}\].  This is known as the scalar product form of a plane.

 

 

(12) Vector equation of a plane normal to unit vector \[\mathbf{\hat{n}}\] and at a distance d from the origin is \[\mathbf{r}\mathbf{.\hat{n}}=d\].

 

 

If \[\mathbf{n}\] is not a unit vector, then to reduce the equation \[\mathbf{r}.\mathbf{n}=d\] to normal form we divide both sides by \[|\mathbf{n}|\] to obtain \[\mathbf{r}\cdot \frac{\mathbf{n}}{|\mathbf{n}|}=\frac{d}{|\mathbf{n}|}\] or \[\mathbf{r}.\mathbf{\hat{n}}=\frac{d}{|\mathbf{n}|}\].

 

 

(13) The equation of the plane passing through a point having position vector \[\mathbf{a}\] and parallel to \[\mathbf{b}\] and \[\mathbf{c}\] is \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}+\mu \mathbf{c}\]or \[[\mathbf{r}\,\mathbf{b}\ \mathbf{c}]=[\mathbf{a}\,\mathbf{b}\ \mathbf{c}]\], where \[\lambda \] and \[\mu \] are scalars.

 

 

(14) Vector equation of a plane passing through a point \[\mathbf{a,}\,\mathbf{b,}\,\mathbf{c}\] is \[\mathbf{r}=(1-s-t)\,\mathbf{a}+s\,\mathbf{b}\,t\,+\,\mathbf{c}\]or \[\mathbf{r}.\,(\mathbf{b}\times \,\mathbf{c}+\,\mathbf{c}\times \mathbf{a}+\mathbf{a}\times \,\mathbf{b}\,)=[\mathbf{a}\,\mathbf{b}\,\mathbf{c}]\].

 

 

(15) The equation of any plane through the intersection of planes \[\mathbf{a},\,\mathbf{b},\,\mathbf{c},\,\mathbf{d}\] and \[x\mathbf{a}+y\mathbf{b}+z\mathbf{c}+u\mathbf{d}=\mathbf{0}\] is \[\mathbf{r}.({{\mathbf{n}}_{1}}+\lambda {{\mathbf{n}}_{2}})={{d}_{1}}+\lambda {{d}_{2}}\], where \[\lambda \] is an arbitrary constant.

 

 

(16) The perpendicular distance of a point having position vector \[\mathbf{a}\] from the plane \[\mathbf{r}.\mathbf{n}=d\] is given by \[p=\frac{|\mathbf{a}.\mathbf{n}-d|}{|\mathbf{n}|}\].

 

 

(17) An angle q between the planes \[{{\mathbf{r}}_{1}}.{{\mathbf{n}}_{1}}={{d}_{1}}\] and \[{{\mathbf{r}}_{2}}.{{\mathbf{n}}_{2}}={{d}_{2}}\] is given by \[\cos \theta =\pm \frac{{{\mathbf{n}}_{1}}.{{\mathbf{n}}_{2}}}{|{{\mathbf{n}}_{1}}||{{\mathbf{n}}_{2}}|}\].

 

 

(18) Perpendicular distance of a point \[P\,(\mathbf{r})\] from a line passing through \[\mathbf{a}\] and parallel to \[\mathbf{b}\] is given by \[PM=\frac{|\,(\mathbf{r}-\mathbf{a})\times \mathbf{b}\,|}{|\mathbf{b}|}\] \[={{\left[ {{(\mathbf{r}-\mathbf{a})}^{2}}-{{\left\{ \frac{(\mathbf{r}-\mathbf{a})\,.\mathbf{b}}{|\mathbf{b}|} \right\}}^{2}} \right]}^{1/2}}\].

 

 

(19) The equation of the planes bisecting the angles between the planes \[{{\mathbf{r}}_{\mathbf{1}}}.{{\mathbf{n}}_{\mathbf{1}}}={{d}_{1}}\] and \[{{\mathbf{r}}_{2}}.{{\mathbf{n}}_{2}}={{d}_{2}}\] are \[\frac{|\mathbf{r}.{{\mathbf{n}}_{\mathbf{1}}}-{{d}_{1}}|}{|{{\mathbf{n}}_{\mathbf{1}}}|}\] \[=\frac{|\mathbf{r}.{{\mathbf{n}}_{2}}-{{d}_{2}}|}{|{{\mathbf{n}}_{2}}|}\]

 

 

 

or \[\frac{\mathbf{r}.{{\mathbf{n}}_{\mathbf{1}}}-{{d}_{1}}}{|{{\mathbf{n}}_{\mathbf{1}}}|}\]\[=\pm \frac{\mathbf{r}.{{\mathbf{n}}_{2}}-{{d}_{2}}}{|{{\mathbf{n}}_{2}}|}\]

 

 

or \[\mathbf{r}.({{\mathbf{n}}_{1}}\pm {{\mathbf{n}}_{\mathbf{2}}})=\frac{{{d}_{1}}}{|{{\mathbf{n}}_{\mathbf{1}}}|}\pm \frac{{{d}_{2}}}{|{{\mathbf{n}}_{2}}|}\].

 

 

(20) Perpendicular distance of a point \[P\,(\mathbf{r})\] from a plane passing through a point \[\mathbf{a}\] and parallel to \[\mathbf{b}\] and \[\mathbf{c}\] is given by \[PM=\frac{\,(\mathbf{r}-\mathbf{a}).(\mathbf{b}\times \mathbf{c})}{|\mathbf{b}\times \mathbf{c}|}\].

 

 

(21) Perpendicular distance of a point \[P(\mathbf{r})\] from a plane passing through the points \[\mathbf{a},\,\mathbf{b}\] and \[\mathbf{c}\] is given by  \[PM=\frac{(\mathbf{r}-\mathbf{a})\,.\,(\mathbf{b}\times \mathbf{c}+\mathbf{c}\times \mathbf{a}+\mathbf{a}\times \mathbf{b})}{|\mathbf{b}\times \mathbf{c}+\mathbf{c}\times \mathbf{a}+\mathbf{a}\times \mathbf{b}|}\].

 

 

(22) Angle between line and plane : If \[\theta \] is the angle between a line \[\mathbf{r}=(\mathbf{a}+\lambda \mathbf{b})\] and the plane \[\mathbf{r}.\mathbf{n}=d\], then \[\sin \theta =\frac{\mathbf{b}.\mathbf{n}}{|\mathbf{b}||\mathbf{n}|}\].

 

 

(i) Condition of perpendicularity: If the line is perpendicular to the plane, then it is parallel to the normal to the plane. Therefore \[\mathbf{b}\] and \[\mathbf{n}\] are parallel.

 

 

So, \[\mathbf{b}\times \mathbf{n}=0\] or \[\mathbf{b=\lambda n}\] for some scalar \[\lambda \].

 

 

(ii) Condition of parallelism : If the line is parallel to the plane, then it is perpendicular to the normal to the plane. Therefore \[\mathbf{b}\] and \[\mathbf{n}\] are perpendicular. So, \[\mathbf{b}\mathbf{.n}=0\].

 

 

(iii) If the line \[\mathbf{r}=\mathbf{a}+\lambda \mathbf{b}\] lies in the plane \[\mathbf{r}\mathbf{.n}=d,\] then

 

 

(a)  \[\mathbf{b}\mathbf{.n}=0\]                      

 

 

(b)  \[\mathbf{a}\mathbf{.n}=d\].

 

 

(23) The equation of sphere with centre at \[C(\mathbf{c})\] and radius \['a'\] is \[|\mathbf{r}-\mathbf{c}|\,=a\].

 

 

(24) The plane \[\mathbf{r}.\mathbf{n}=d\] touches the sphere \[|\mathbf{r}-\mathbf{a}|\,=R\], if \[\frac{|\mathbf{a}.\mathbf{n}-d|}{|\mathbf{n}|}=R\].

 

 

(25) If the position vectors of the extremities of a diameter of a sphere are \[\mathbf{a}\] and \[\mathbf{b,}\] then its equation is \[(\mathbf{r}-\mathbf{a}).(\mathbf{r}-\mathbf{b})=0\] or \[|\mathbf{r}{{|}^{2}}-\mathbf{r}.(\mathbf{a}-\mathbf{b})+\mathbf{a}.\mathbf{b}=0\].