10th Class Mathematics Coordinate Geometry Co-ordinate Geometry

CO-ORDINATE GEOMETRY

FUNDAMENTALS

Co – ordinate geometry is a branch of science which establishes relationship between the position r a point in a plane and pair of algebraic numbers, called its co – ordinates.

Cartesian Co – ordinates

Let us draw coordinate axes with ‘O’ as origin. In Cartesian co-ordinates, the position of a point P - determined by knowing its horizontal and vertical distance from origin.

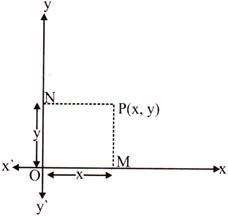
Draw PM and PN perpendiculars on OX and OY respectively. OM is called the x co – ordinate or abscissa of the point P. ON is called the y co – ordinate or the ordinate of the point P.

The abscissa and ordinate of a point are known as co – ordinates of the point P.

If OM = x, ON = y, then the co-ordinates of the point P are (x, y)

OX and OY are called as x – axis and y – axis, respectively and together, they are known as co – ordinate axes.

• Origin ‘O’ is intersection of the axes of co – ordinates. The co – ordinates of the point O are O (0, 0)
• The distance of the point P from y – axis is called its abscissa. In the figure OM is the abscissa.
• The distance of the point P from x – axis is called its ordinate. ON is the ordinate in the figure.

Quadrant

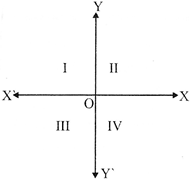
A quadrant is \[\frac{1}{4}\] part of a plane divided by the co – ordinate axes.

(a) XOY is called the first quadrant, (or Ist quadrant)

(b) YOX', the second. (II nd quadrant)

(c) X'OY', the third. (III rd quadrant)

(d) Y'OX, the fourth. (IV th quadrant)

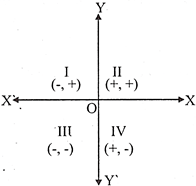
Sign Convention in different quadrants

(a) In the first quadrant, both co-ordinates i.e., abscissa and ordinate of a point are positive.

(b) In the second quadrant, abscissa is negative and ordinate is positive.

(c) In the third quadrant, for a point, both abscissa and ordinate are negative.

(d) In the fourth quadrant, the abscissa is positive and the ordinate is negative.

Distance between two points \[{{P}_{1}}\]& \[{{P}_{2}}\]

\[\therefore \] \[{{P}_{1}}{{P}_{2}}=\sqrt{\left( {{x}_{2}}-{{x}_{1}} \right){{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}\] where \[\left( {{x}_{1}},\text{ }{{y}_{1}} \right)\] & \[\left( {{x}_{2}},\text{ }{{y}_{2}} \right)\] are coordinates of \[{{P}_{1}}\]& \[{{P}_{2}}\]

Ratio formula for internal and external Division (Section Formula)

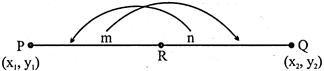
The Co – ordinates of a point R which divides the straight line joining two points \[P\left( {{x}_{1}},{{y}_{1}} \right)\] and  \[Q\left( {{x}_{2}},{{y}_{2}} \right)\] internally in the ratio \[m:n\]are

Where, \[\frac{PR}{QR}=\frac{m}{n}\]

Coordinates of R are given by, \[R\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\];

This formula can be easily remembered if we look at the following diagram:

Special Cases:

1. If R is the mid-point of AB, then it will divide AB in the ratio of \[1:1\], and its co – ordinates are

\[R\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]

1. External Division: The co-ordinates of a point which divides the straight line joining two points \[\left( {{x}_{1}},\text{ }{{y}_{1}} \right)\] and \[\left( {{x}_{2}},\text{ }{{y}_{2}} \right)\] externally in the ratio \[m:n\]are \[R\left( \frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n} \right)\]

• While solving problems, \[m:n\]is written as \[K:1\](Where, \[K=\frac{m}{n}\]).

This straightaway reduces two variables (m & n) to one variable (K).

Thus, R will become \[R\left( \frac{K{{x}_{2}}+{{x}_{1}}}{K+1},\frac{K{{y}_{2}}+{{y}_{1}}}{K+1} \right)\]

Co-ordinates of the Centroid of a triangle

Let a \[\Delta \,ABC\], have its vertices as \[A\left( {{x}_{1}},\text{ }{{y}_{1}} \right),\text{ }B\left( {{x}_{2}}-{{y}_{2}} \right)\] and  \[C\left( {{x}_{3}}-{{y}_{3}} \right)\].

The medians of a triangle are concurrent and the point of concurrence is called centroid. The centroid divides each median in the ratio of \[2:1\].

If G is the centroid, then \[AG:GD-2:1\]

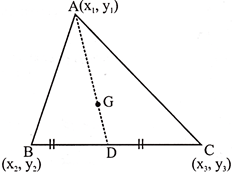
The co-ordinates of the centroid are given as

\[G\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\]

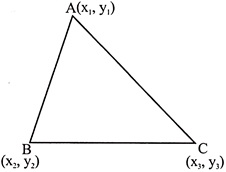
Area of a triangle in terms of co-ordinates of its vertices

Let \[A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)\] and \[C\left( {{x}_{3}},{{y}_{3}} \right)\] be the vertices of \[\Delta \,ABC,\]

Area of \[\Delta \,ABC,\] is given by\[=\frac{1}{2}\left[ {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)+{{x}_{2}}\left( {{y}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right]\]

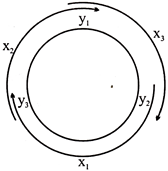
(See the above circular diagram to remember this formula).

The area can also be written as, area of a triangle \[=\frac{1}{2}\]

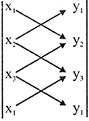
\[=\frac{1}{2}\left[ \left( {{x}_{1}}{{y}_{2}}-{{x}_{2}}{{y}_{1}} \right)+\left( {{x}_{2}}{{y}_{3}}-{{x}_{3}}{{y}_{2}} \right)+\left( {{x}_{3}}{{y}_{1}}-{{x}_{1}}{{y}_{3}} \right) \right]\]

Condition for Collinearity of three points

Three points \[A\left( {{x}_{1}},\text{ }{{y}_{1}} \right),\text{ }B\left( {{x}_{2}},\text{ }{{y}_{2}} \right)\] and \[C\left( {{x}_{3}},{{y}_{3}} \right)\]lie on a straight line or are collinear ‘iff’ the area of the triangle formed by them is zero. (Word ‘iff means, ‘if and only if’). This means that both the statement and its converse are true. Thus, (i) if area of Ale formed by A, B, C = 0, then A, B, C are collinear and (ii) if A, B, C are collinear, then area of \[\Delta le\,\,ABC=0\] (Also, refer to chapter___ of GMO class – 10 of this book to further understand the use of' ‘iff’ in a different situation). We can also write the condition as, \[{{x}_{1}}\left( {{y}_{2}},{{y}_{3}} \right)+{{x}_{2}}\left( {{\text{y}}_{3}}-{{y}_{1}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right)=0\]