Distance Between two Points
Category : 10th Class
Let us consider the two points \[A({{x}_{1}}{{y}_{1}}),\And B({{x}_{2}},{{y}_{2}}),\] in a two dimensional plane, then the distance between the two points is given by \[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]. If it is a three dimensional plane containing the points \[A({{x}_{1}},{{y}_{1}},{{z}_{1}})\And B({{x}_{2}},{{y}_{2}},{{z}_{2}},{{z}_{2}}),\] then the distance between the points is given by: \[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}+{{({{z}_{2}}-{{z}_{1}})}^{2}}}\]
![]() Proof of Finding Distance Between Two Points
Proof of Finding Distance Between Two Points
Let \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] be the given points.
Draw AL \[\bot \] OX and AN \[\bot \] BM
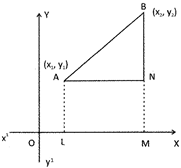
Now, from Figure
\[OL={{X}_{1}},OM={{X}_{2}},AL={{Y}_{1}}\And BM={{Y}_{2}}\].
\[\therefore \,\,\,AN=LM=(OM-OL)={{X}_{2}}-{{X}_{1}}\]
BN = (BM - NM) = (BM - AL) \[={{Y}_{2}}-{{Y}_{1}}\,\,[\therefore \,NM=AL]\]
From right \[\Delta ANB\], By Pythagorean" theorem, we have \[A{{B}^{2}}=(A{{N}^{2}}+B{{M}^{2}})\]
\[\Rightarrow \,\,{{(AB)}^{2}}={{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}\]
\[\Rightarrow \,\,(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Hence, the distance between the points \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] given by:
\[(AB)=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{Y}_{2}}-{{Y}_{1}})}^{2}}}\]
Section Formula
Let us consider the point P(X, Y) which divides the line segment joining \[A({{x}_{1}},{{x}_{1}})\And B({{x}_{2}}-{{y}_{2}})\] in the ratio m : n, then the coordinate of the point P is given by:
\[X=\frac{m{{x}_{1}}n{{x}_{2}}}{m+n}and\,\,y=\frac{m{{y}_{1}}+n{{y}_{2}}}{m+n}\]
Proof
Let \[A({{x}_{1}},{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\]be the two points and let P(X, Y) divides it in the ratio m:n, then,
\[\frac{AP}{PB}=\frac{m}{n}\]
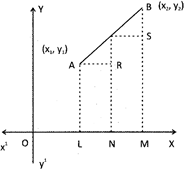
Draw \[AL\bot OX;BM\bot OX;PN\bot OX,AR\bot PN,\And PS\bot \]BM.
Now, \[AR=LM=ON=OL=({{x}_{1}}-{{x}_{2}})\]
\[PS=NM=OM=ON=({{x}_{2}}-x)\]
\[PR=PN-RN=PN-AL=(y-{{y}_{1}})\]
\[BS=MB-SM=BM-PN=({{y}_{2}}-y)\]
Clearly \[\Delta ARP\,and\,\Delta PSB\] are similar & their sides are in proportional.
\[\therefore \,\,\,\,\,\frac{AP}{PB}=\frac{AR}{PS}=\frac{PR}{BS}\]
\[\Rightarrow \,\,\,\,\,\frac{m}{n}=\frac{x-{{x}_{1}}}{{{x}_{2}}-x}=\frac{y-{{y}_{2}}}{{{y}_{2}}-y}\]
\[\Rightarrow \,\,\,\,x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}and\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]
Hence the coordinate of the point \[P\left( x=\frac{m{{x}_{2}}+n{{x}_{1}}}{m+n}and\,y=\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \right)\]
![]() Coordinate of Midpoint
Coordinate of Midpoint
The coordinate of the mid-point M of a line segment AB with coordinate \[A({{x}_{1}}-{{y}_{1}})\And B({{x}_{2}},{{y}_{2}})\] is given by \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2}\,and\,\,\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
Proof
The mid-point of a line segment joining two points divide it into two equal parts, so the ratio is 1 : 1.
So, by the section formula, the coordinates of the \[\left( \frac{1.{{x}_{2}}+1.{{x}_{1}}}{1+1},\frac{1.{{y}_{2}}+{{y}_{2}}}{1+1} \right)\] i.e \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\]
Hence, the coordinates of the midpoint of AB are. \[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2} \right)\].
![]() Centroid of a Triangle
Centroid of a Triangle
If is defined as the point of intersection of the medians of the triangle. To find the coordinates of the centroid of the triangles, we have, Let \[A({{x}_{1}},{{y}_{2}})B({{x}_{2}},{{y}_{2}})\And C({{x}_{3}},{{y}_{3}})\] be the vertices of a AABC. Let D be the midpoint of BC. Then, the coordinates of the point D is given by:
\[=\left( \frac{{{x}_{2}}+{{x}_{3}}}{2},\frac{{{y}_{2}}+{{y}_{3}}}{2} \right)\]
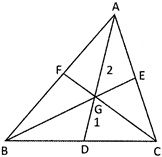
Let G (x, y) be the centroid of A ABC.
Then, G divides AD in the ratio 2 : 1.
\[\therefore \,\,\,\,x=\left\{ \frac{2\frac{({{x}_{2}}+{{x}_{3}})}{2}+1.{{x}_{1}}}{2+1} \right\}=\frac{({{x}_{1}}+{{x}_{2}}+{{x}_{3}})}{3}\]
\[y=\left\{ \frac{2\frac{({{y}_{2}}+{{y}_{3}})}{2}+1.{{y}_{3}}}{2+1} \right\}=\frac{({{y}_{1}}+{{y}_{2}}+{{y}_{3}})}{3}\]
Hence the coordinates of G are \[\left( \frac{({{x}_{1}}+{{x}_{2}}{{+}_{3}}}{3},\frac{({{y}_{1}}+{{y}_{2}}+{{y}_{3}})}{3} \right)\].
![]() Area of the Triangle
Area of the Triangle
Let \[A({{x}_{1}},{{y}_{1}})B({{x}_{3}},{{y}_{2}})\And C({{x}_{3}},{{y}_{3}})\]be the vertices of the triangle, then the area of the triangle is given by: Area \[=\frac{1}{2}\left| {{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}\left. ) \right| \right.\]
Proof
Let \[A({{x}_{1}},{{y}_{2}}),B({{x}_{2}},{{y}_{2}})\And C({{x}_{3}},{{y}_{3}})\] be the vertices of the given A ABC. Draw AL, BM & CN perpendicular to the x - axis.
Then, \[ML=({{x}_{1}}-{{x}_{2}}),Ln=({{x}_{3}}-{{x}_{1}})\And MN=({{x}_{3}}-{{x}_{2}})\]
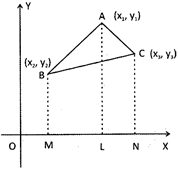
\[\begin{align} & \therefore \,\,Area\,(\Delta ABC)=ar(trapBMLA)+ar(trapALNO) \\ & -ar(trapBMNC) \\ \end{align}\]
\[=\left\{ \frac{1}{2}(AL+BM)\times ML \right\}+\left\{ \frac{1}{2}(AL+CN)\times LN \right\}-\left\{ \frac{1}{2}(BM+CN)\times MN \right\}.\]
\[=\frac{1}{2}({{y}_{1}}+{{y}_{2}})\,({{x}_{1}}-{{x}_{2}})+\frac{1}{2}({{y}_{1}}+{{y}_{3}})\,({{x}_{3}}-{{x}_{1}})-\frac{1}{2}({{y}_{2}}+{{y}_{3}})\,({{x}_{3}}-{{x}_{2}}).\]
Ar. \[(\Delta ABC)=\frac{1}{2}\left| \left. {{x}_{1}}({{y}_{2}}-{{y}_{3}}+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2)}}) \right|. \right.\]
![]() Condition for Collinearity of Three Points
Condition for Collinearity of Three Points
Let the given points be A \[A({{x}_{1}},{{y}_{2}})B,({{x}_{2}},{{y}_{2}})\And C({{x}_{3}},{{y}_{3}})\] .If A, B & C are collinear then. Area (\[\Delta \] ABC) = 0.
\[\Rightarrow \,\,\,\,\frac{1}{2}\left| \left. {{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{2}}) \right|=0 \right.\]
![]() Coordinate of In center
Coordinate of In center
Lf \[A({{x}_{1}},{{y}_{2}}),B({{x}_{2}},{{y}_{2}})\And C({{x}_{3}},{{y}_{3}})\] be the coordinate of the vertices of the A (ABC), having side length' a, b, c,' then the incentre of the triangle is given by:
\[I=\left( \frac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\frac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\]

![]() Find the coordinates of the point which divides the line segment Joining the points A(4 - 3) & B(9,7) in the ratio 3 : 2.
Find the coordinates of the point which divides the line segment Joining the points A(4 - 3) & B(9,7) in the ratio 3 : 2.
(a) (7, 3)
(b) (5, 3)
(c) (4, 3)
(d) (2, 3)
(e) None of these
Answer: (a)
Explanation
The coordinate of the points are A(4-3) &B(9,7)
Also m : n = 3 : 2
![]()
Let the coordinate of the point be P(x, y)
Then by section formula, we have
\[x=\frac{m{{X}_{1}}+n{{X}_{2}}}{m+n}and\,y=\frac{m{{Y}_{1}}+n{{Y}_{2}}}{m+n}\]
\[x=\frac{(3\times 9+2\times 4)}{(3+2)},y=\frac{\{3\times 7+2(-3)\}}{(3+2)}\]
\[x=7,y=3\].
Hence the required point is P (7, 3)
![]() Find the distance between the points A (7, 13) & B (10, 9).
Find the distance between the points A (7, 13) & B (10, 9).
(a) 2 units
(b) 3 units
(c) 5 units
(d) 7 units
(e) None of these
Answer: (c)
Explanation
The given points are A (7,13) & B(10, 9).
Here we have,
\[({{x}_{1}}=7,{{y}_{1}}=13)\And ({{x}_{2}}=10,{{y}_{2}}=9)\]
Now the distance is given by:
\[AB=\sqrt{{{({{x}_{2}}-{{x}_{1}})}^{2}}+{{({{y}_{2}}-{{y}_{1}})}^{2}}}\]
\[=\sqrt{{{(10-7)}^{2}}+{{(9-13)}^{2}}}\]
\[=\sqrt{9+16}=\sqrt{25}=5\,unit\]
![]() Find the coordinates of the mid-point of the line segment joining the points A(-5,4) & B(7,-8).
Find the coordinates of the mid-point of the line segment joining the points A(-5,4) & B(7,-8).
(a) (3, -2)
(b) (1, -2)
(c) (1, 4)
(d) (3, 4)
(e) None of these
Answer: (b)
Explanation
Let M (x, y) be the midpoint of AB.
Then \[x=\frac{-5+7}{2}=1\,\,and\,\,y=\frac{4-8}{2}=-2\]
Hence the mid- point is M (1, -2)
![]() Find the area of the triangle whose vertices are A (2, 7), B (3,-l) & C(-5, 6).
Find the area of the triangle whose vertices are A (2, 7), B (3,-l) & C(-5, 6).
(a) 18 sq. units
(b) 24 sq. units
(c) 22 sq. units
(d) 28 sq. units
(e) None of these
Answer: (d)
Explanation
We have the coordinate of the vertices of the triangle\[\Delta ABC\,as\,A(2,7),B(3,-1)\And C(-5,\,6)\].
Then \[{{x}_{1}}=2,{{y}_{1}}=7,({{x}_{2}}=3,{{y}_{2}}=-1)\And ({{x}_{3}}=-5,{{x}_{3}}=6)\]
Area \[\Delta \]ABC \[=\frac{1}{2}\left| \left. {{x}_{1}}({{y}_{2}}-{{y}_{3}})+{{x}_{2}}({{y}_{3}}-{{y}_{1}})+{{x}_{3}}({{y}_{1}}-{{y}_{2}}) \right| \right.\]
\[=\frac{1}{2}\left| \left. 2(-1-6)+3(6-7)-5(7+1) \right| \right.\]
\[=\frac{1}{2}\left|\left. -14-12-30 \right|=\frac{56}{2}= \right.28\] Sq units
![]() Find the value of 'K' for which the points A (2, 3) B (5, K) & C (6, 7) are collinear.
Find the value of 'K' for which the points A (2, 3) B (5, K) & C (6, 7) are collinear.
(a) 4
(b) 6
(c) \[\frac{-3}{2}\]
(d) \[\frac{11}{4}\]
(e) None of these
Answer: (b)
Explanation
Since the points are collinear so area (\[\Delta \]ABC) = 0
\[\Rightarrow \,\,\,\frac{1}{2}\left| \left. 2(K-7)+5(7-3)+6(3-K) \right|=0 \right.\]
\[\Rightarrow \,\,\,4K-24=0\]
\[\Rightarrow \,\,\,4K=24\]
\[\Rightarrow \,\,\,K=6\]
![]() Find the centroid of \[\Delta \] ABC whose vertices are A (-3, 0) B (5, -2) and C (- 8, 5).
Find the centroid of \[\Delta \] ABC whose vertices are A (-3, 0) B (5, -2) and C (- 8, 5).
(a) (-2, 1)
(b) (2, 1)
(c) (3, 5)
(d) (3, 5)
(e) None of these
Answer: (a)
Explanation
We have, \[{{x}_{1}}=-3,{{y}_{1}}=0,{{x}_{2}}=5,{{y}_{2}}=-2\,and\,{{x}_{3}}=-8,{{y}_{3}}=5\]
Let G(x, y) be centroid of \[\Delta \] ABC, then \[x=\frac{1}{3}({{x}_{1}}+{{x}_{2}}+{{x}_{3}})\,and\,y=\frac{1}{3}({{y}_{1}}+{{y}_{2}}+{{y}_{3}})\]
\[\Rightarrow \,\,x=\frac{-3+5-8}{3}=-2\,and\ =\frac{0-2+5}{3}=1\]
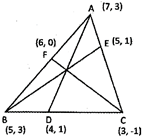
![]() Find the lengths of the medians AD of the A \[\Delta ABC\] whose vertices are A(7, 3), B(5, 3) and C(3, -1), where D is the midpoint of the side BC.
Find the lengths of the medians AD of the A \[\Delta ABC\] whose vertices are A(7, 3), B(5, 3) and C(3, -1), where D is the midpoint of the side BC.
(a) 5
(b) 6
(c) 10
(d) 9
(e) None of these
Answer: (a)
Explanation
Since D is the mid-point of the side BC of the triangle \[\Delta ABC\], then we have the coordinate of the point D is given by:
\[D\left( \frac{5+3}{2}=4\frac{3+(-1)}{2}=1 \right)\]
i.e., D (4, 1)
Therefore the length of the medians AD is given by:
\[AD=\sqrt{{{(4-7)}^{2}}{{(1+3)}^{2}}}=\sqrt{{{(3)}^{2}}+{{4}^{2}}}=\sqrt{25}=5\]units
![]() Let D (3, 2), E (-3, 1) & F (4 - 3) be the midpoints of the sides BC, CA & AB respectively of \[\Delta ABC\]. Find the coordinates of the vertex A of the \[\Delta ABC\].
Let D (3, 2), E (-3, 1) & F (4 - 3) be the midpoints of the sides BC, CA & AB respectively of \[\Delta ABC\]. Find the coordinates of the vertex A of the \[\Delta ABC\].
(a) (10,-6)
(b) (-2, 0)
(c) (-4,2)
(d) (5, -3)
None of these
Answer: (b)
Explanation
Let the coordinate of the vertices of the triangle be given by \[A\left( {{x}_{1}},{{y}_{1}} \right)\], \[B({{x}_{2,}}{{y}_{2}})\And C({{x}_{3}},{{y}_{3}})\]
The coordinate of the midpoints of the sides BC, CA & AB of the triangle are given as D (3, 2), E (-3, 1) & F (4, 3) respectively
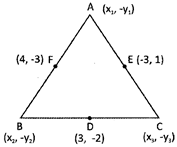
Since D is the mid-points of BC
Therefore, coordinate of D is given by:
\[\Rightarrow \,\,\frac{{{x}_{2}}+{{x}_{3}}}{2}=3,\frac{{{y}_{3}}+{{y}_{3}}}{2}=2\]
\[\Rightarrow \,\,{{x}_{2}}+{{x}_{3}}=6\,.................(i)\,and\,{{y}_{3}}=-4\,............(ii)\]
Again E in the mid-point of CA, therefore, coordinate of E is given by:
\[\Rightarrow \,\,\,\frac{{{x}_{1}}+{{x}_{3}}}{2}=-3\frac{{{y}_{1}}+{{y}_{3}}}{2}=-1\]
\[{{x}_{1}}+{{x}_{3}}=-6.......(iii),\,and\,{{y}_{1}}+{{y}_{3}}=2\,.......\,(iv)\]
And F is the mid-point of AB, therefore, coordinate of F is given by:
\[\Rightarrow \,\,\frac{{{x}_{1}}+{{x}_{2}}}{2}=4\frac{{{y}_{2}}+{{y}_{2}}}{2}=-3\]
\[\Rightarrow \,\,\,{{x}_{1}}+{{x}_{2}}=8\,........\,(v)\,\,and\,({{y}_{1}}+{{y}_{2}}=6........(iv)\]
Solving the above equations we get,
\[({{x}_{1}}=-2,{{x}_{2}}=10,{{x}_{3}}=4)\,and\,({{y}_{1}}=0,{{y}_{2}}=-6,{{y}_{3}}=2)\]
Therefore, coordinate of the vertex A (-2, 0)
![]() If A (-2, -1), B (a, 0), C (4, b) & D (1, 2) are the vertices of a parallelogram, then find the values of a & b.
If A (-2, -1), B (a, 0), C (4, b) & D (1, 2) are the vertices of a parallelogram, then find the values of a & b.
(a) a = 3, b = - 3
(b) a = 3, b = 5
(c) a = 1, b = - 3
(d) a = 1, b = 3
(e) None of these
Answer: (d)
Explanation
We have the vertices of the parallelogram as A (-2, -1), B (a, 0), C (4, b) & D (1, 2).
Then AC & BD are the diagonals, intersecting each other at the point O Since we know that '0' is the midpoint of the diagonal AC and BD, as the diagonal of the parallelogram bisect each other,
Therefore, mid-point of \[AC=\left( \frac{-2+4}{2},\frac{-1+b}{2} \right)=\left( 1,\frac{b-1}{2} \right)\]
And the mid-point of \[BD=\left( \frac{a+1}{2},\frac{0+2}{2} \right)=\left( \frac{a+1}{2},1 \right)\]
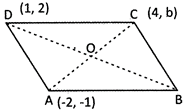
\[\therefore \,\,\,\,\,\,\frac{a+1}{2}=1\,\,\,\And \,\,\frac{b-1}{2}=1\]
\[\Rightarrow \,\,\,\,a=1\,\,\And \,\,b=3\]
You need to login to perform this action.
You will be redirected in
3 sec
